|
Fundamental (music)
The fundamental frequency, often referred to simply as the ''fundamental'', is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In terms of a superposition of sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc. In this context, the zeroth harmonic would be 0 Hz.) According to Benward's and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are periodic. The period of a waveform is the smallest value of T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Partials On Strings
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the other harmonics are known as ''higher harmonics''. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a '' harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz. In music, harmonics are used on string instruments and wind instrum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MIT Press
The MIT Press is a university press affiliated with the Massachusetts Institute of Technology (MIT) in Cambridge, Massachusetts (United States). It was established in 1962. History The MIT Press traces its origins back to 1926 when MIT published under its own name a lecture series entitled ''Problems of Atomic Dynamics'' given by the visiting German physicist and later Nobel Prize winner, Max Born. Six years later, MIT's publishing operations were first formally instituted by the creation of an imprint called Technology Press in 1932. This imprint was founded by James R. Killian, Jr., at the time editor of MIT's alumni magazine and later to become MIT president. Technology Press published eight titles independently, then in 1937 entered into an arrangement with John Wiley & Sons in which Wiley took over marketing and editorial responsibilities. In 1962 the association with Wiley came to an end after a further 125 titles had been published. The press acquired its modern name af ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Tuning
In music, there are two common meanings for tuning: * Tuning practice, the act of tuning an instrument or voice. * Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases. Tuning practice Tuning is the process of adjusting the pitch of one or many tones from musical instruments to establish typical intervals between these tones. Tuning is usually based on a fixed reference, such as A = 440 Hz. The term "''out of tune''" refers to a pitch/tone that is either too high (sharp) or too low (flat) in relation to a given reference pitch. While an instrument might be in tune relative to its own range of notes, it may not be considered 'in tune' if it does not match the chosen reference pitch. Some instruments become 'out of tune' with temperature, humidity, damage, or simply time, and must be readjusted or repaired. Different methods of sound production require different methods of adjustment: * Tuning to a pitch with one's voic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Of Harmonics
The scale of harmonics is a musical scale based on the noded positions of the natural harmonics existing on a string. This musical scale is present on the guqin, regarded as one of the first string instruments with a musical scale.Yin, Wei. ''Zhongguo Qinshi Yanyi'' 【中国琴史演义】 (Chinese). Pages 1-10. Most fret positions appearing on Non-Western string instruments (lutes) are equal to positions of this scale. Unexpectedly, these fret positions are actually the corresponding undertones of the overtones from the harmonic series. The distance from the nut to the fret is an integer number lower than the distance from the fret to the bridge (see: superparticular number). Origin On the guqin, the left end of the dotted scale is a mirror image of the right end. The instrument is played with flageolet tones (harmonics) as well as pressing the strings on the wood. The flageolets appear on the harmonic positions of the overtone series, therefore these positions are marked as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pitch Detection Algorithm
Pitch may refer to: Acoustic frequency * Pitch (music), the perceived frequency of sound including "definite pitch" and "indefinite pitch" ** Absolute pitch or "perfect pitch" ** Pitch class, a set of all pitches that are a whole number of octaves apart ** Relative pitch, the ability to identify a given musical interval between two notes * Pitch accent, a form of accentuation in speech Business * Sales pitch, a line of talk that attempts to persuade someone or something ** Pitch (filmmaking), a proposal for a film ** Elevator pitch, a very short sales presentation, allegedly short enough to be made during an elevator ride Measurement Movement about the transverse axis * Pitch angle (or pitch rotation), one of the angular degrees of freedom of any stiff body (for example a vehicle), describing rotation about the side-to-side axis ** Pitch (aviation), one of the aircraft principal axes of rotation (nose-up or nose-down angle measured from horizontal axis) ** Pitch (ship motion), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillation
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms. Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, geothermal geysers in geology, vibration of strings in guitar and other string instruments, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy. The term ''vibration'' is precisely used to describe a mechanical oscillation. Oscillation, especially rapid oscillation, may be an undesirable phenomenon in proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Frequency
Natural frequency, also known as eigenfrequency, is the frequency at which a system tends to oscillate in the absence of any driving force. The motion pattern of a system oscillating at its natural frequency is called the normal mode (if all parts of the system move sinusoidally with that same frequency). If the oscillating system is driven by an external force at the frequency at which the amplitude of its motion is greatest (close to a natural frequency of the system), this frequency is called resonant frequency. Overview Free vibrations of an elastic body are called ''natural vibrations'' and occur at a frequency called the natural frequency. Natural vibrations are different from forced vibrations which happen at the frequency of an applied force (forced frequency). If the forced frequency is equal to the natural frequency, the vibrations' amplitude increases manyfold. This phenomenon is known as resonance. In a mass-spring system, with mass ''m'' and spring stiffness ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
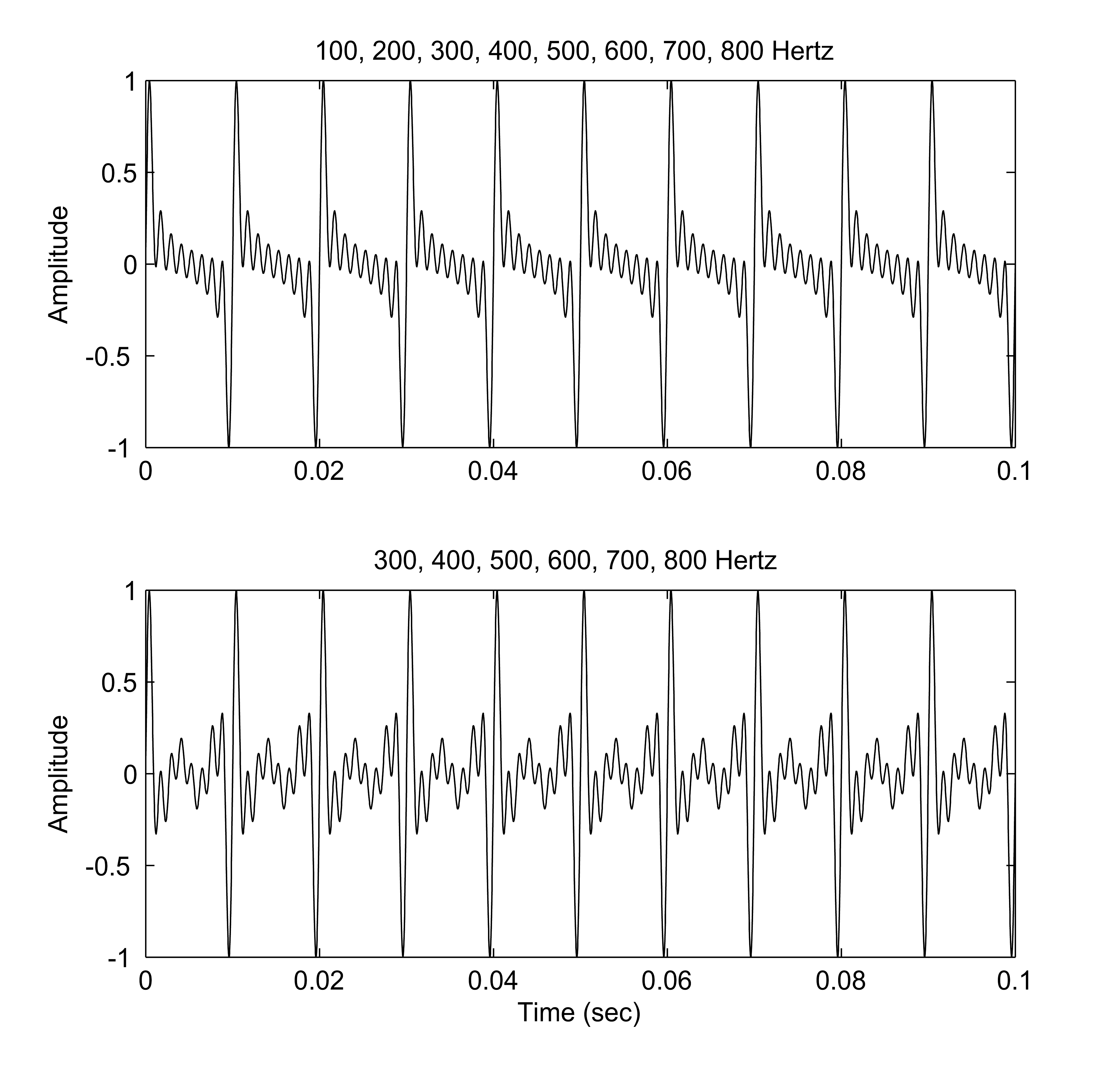
Missing Fundamental
A harmonic sound is said to have a missing fundamental, suppressed fundamental, or phantom fundamental when its overtones suggest a fundamental frequency but the sound lacks a component at the fundamental frequency itself. The brain perceives the pitch of a tone not only by its fundamental frequency, but also by the periodicity implied by the relationship between the higher harmonics; we may perceive the same pitch (perhaps with a different timbre) even if the fundamental frequency is missing from a tone. For example, when a note (that is not a pure tone) has a pitch of 100 Hz, it will consist of frequency components that are integer multiples of that value (e.g. 100, 200, 300, 400, 500.... Hz). However, smaller loudspeakers may not produce low frequencies, and so in our example, the 100 Hz component may be missing. Nevertheless, a pitch corresponding to the fundamental may still be heard. Explanation A low pitch (also known as the pitch of the missing fundamental ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greatest Common Divisor
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers ''x'', ''y'', the greatest common divisor of ''x'' and ''y'' is denoted \gcd (x,y). For example, the GCD of 8 and 12 is 4, that is, \gcd (8, 12) = 4. In the name "greatest common divisor", the adjective "greatest" may be replaced by "highest", and the word "divisor" may be replaced by "factor", so that other names include highest common factor (hcf), etc. Historically, other names for the same concept have included greatest common measure. This notion can be extended to polynomials (see Polynomial greatest common divisor) and other commutative rings (see below). Overview Definition The ''greatest common divisor'' (GCD) of two nonzero integers and is the greatest positive integer such that is a divisor of both and ; that is, there are integers and such that and , and is the largest s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Analysis
Modal analysis is the study of the dynamic properties of systems in the frequency domain. Examples would include measuring the vibration of a car's body when it is attached to a shaker, or the noise pattern in a room when excited by a loudspeaker. Modern day experimental modal analysis systems are composed of 1) sensors such as transducers (typically accelerometers, load cells), or non contact via a Laser vibrometer, or stereophotogrammetric cameras 2) data acquisition system and an analog-to-digital converter front end (to digitize analog instrumentation signals) and 3) host PC (personal computer) to view the data and analyze it. Classically this was done with a SIMO (single-input, multiple-output) approach, that is, one excitation point, and then the response is measured at many other points. In the past a hammer survey, using a fixed accelerometer and a roving hammer as excitation, gave a MISO (multiple-input, single-output) analysis, which is mathematically identical to SI ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vibration
Vibration is a mechanical phenomenon whereby oscillations occur about an equilibrium point. The word comes from Latin ''vibrationem'' ("shaking, brandishing"). The oscillations may be periodic function, periodic, such as the motion of a pendulum—or random, such as the movement of a tire on a gravel road. Vibration can be desirable: for example, the motion of a tuning fork, the Reed (music), reed in a woodwind instrument or harmonica, a mobile phone, or the cone of a loudspeaker. In many cases, however, vibration is undesirable, wasting energy and creating unwanted sound. For example, the vibrational motions of engines, electric motors, or any Machine, mechanical device in operation are typically unwanted. Such vibrations could be caused by Engine balance, imbalances in the rotating parts, uneven friction, or the meshing of gear teeth. Careful designs usually minimize unwanted vibrations. The studies of sound and vibration are closely related. Sound, or pressure waves, are ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |