|
Fully Irreducible Automorphism
In the mathematical subject geometric group theory, a fully irreducible automorphism of the free group ''Fn'' is an element of Out(Fn), Out(''Fn'') which has no periodic conjugacy classes of proper free factors in ''Fn'' (where ''n'' > 1). Fully irreducible automorphisms are also referred to as "irreducible with irreducible powers" or "iwip" automorphisms. The notion of being fully irreducible provides a key Out(''Fn'') counterpart of the notion of a pseudo-Anosov map, pseudo-Anosov element of the mapping class group of a finite type surface. Fully irreducibles play an important role in the study of structural properties of individual elements and of subgroups of Out(''Fn''). Formal definition Let \varphi\in \operatorname(F_n) where n\ge 2. Then \varphi is called ''fully irreducible'' if there do not exist an integer p\ne 0 and a proper free factor A of F_n such that \varphi^p([A])=[A], where [A] is the conjugacy class of A in F_n. Here saying that A is a proper free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
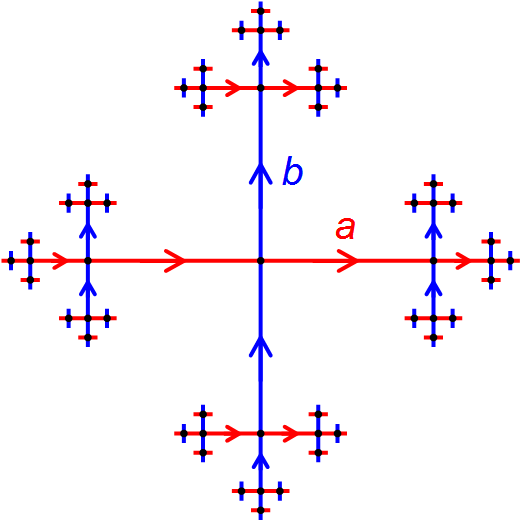
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimensional topology, hyperbolic geometry, algebraic topology, computational group theory and dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometriae Dedicata
''Geometriae Dedicata'' is a mathematical journal, founded in 1972, concentrating on geometry and its relationship to topology, group theory and the theory of dynamical systems. It was created on the initiative of Hans Freudenthal in Utrecht, the Netherlands.. It is published by Springer Netherlands. The Editors-in-Chief An editor-in-chief (EIC), also known as lead editor or chief editor, is a publication's editorial leader who has final responsibility for its operations and policies. The highest-ranking editor of a publication may also be titled editor, managing ... are John R. Parker and Jean-Marc Schlenker.Journal website References External links Springer site Mathematics journals Springer Science+Business Media academic journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bulletin Of The American Mathematical Society
The ''Bulletin of the American Mathematical Society'' is a quarterly mathematical journal published by the American Mathematical Society. Scope It publishes surveys on contemporary research topics, written at a level accessible to non-experts. It also publishes, by invitation only, book reviews and short ''Mathematical Perspectives'' articles. History It began as the ''Bulletin of the New York Mathematical Society'' and underwent a name change when the society became national. The Bulletin's function has changed over the years; its original function was to serve as a research journal for its members. Indexing The Bulletin is indexed in Mathematical Reviews ''Mathematical Reviews'' is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also ..., Science Citation Index, ISI Alerting Services, CompuMath Citation Ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Memoirs Of The American Mathematical Society
''Memoirs of the American Mathematical Society'' is a mathematical journal published in six volumes per year, totalling approximately 33 individually bound numbers, by the American Mathematical Society. It is intended to carry papers on new mathematical research between 80 and 200 pages in length. Usually, a bound number consists of a single paper, i.e., it is a monograph. The journal is indexed by Mathematical Reviews, Zentralblatt MATH, Science Citation Index, Research Alert, CompuMath Citation Index, and Current Contents. Other journals from the AMS * ''Bulletin of the American Mathematical Society'' * ''Journal of the American Mathematical Society'' * ''Notices of the American Mathematical Society'' * ''Proceedings of the American Mathematical Society'' * ''Transactions of the American Mathematical Society The ''Transactions of the American Mathematical Society'' is a monthly peer-reviewed scientific journal of mathematics published by the American Mathematical Society. It ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry & Topology
''Geometry & Topology'' is a peer-refereed, international mathematics research journal devoted to geometry and topology, and their applications. It is currently based at the University of Warwick, United Kingdom, and published by Mathematical Sciences Publishers, a nonprofit academic publishing organisation. It was founded in 1997Allyn Jackson The slow revolution of the free electronic journal Notices of the American Mathematical Society, vol. 47 (2000), no. 9, pp. 1053-1059 by a group of topologists who were dissatisfied with recent substantial rises in subscription prices of journals published by major publishing corporations. The aim was to set up a high-quality journal, capable of competing with existing journals, but with substantially lower subscription fees. The journal was open-access for its first ten years of existence and was available free to individual users, although institutions were required to pay modest subscription fees for both online access and for printed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Advances In Mathematics
''Advances in Mathematics'' is a peer-reviewed scientific journal covering research on pure mathematics. It was established in 1961 by Gian-Carlo Rota. The journal publishes 18 issues each year, in three volumes. At the origin, the journal aimed at publishing articles addressed to a broader "mathematical community", and not only to mathematicians in the author's field. Herbert Busemann writes, in the preface of the first issue, "The need for expository articles addressing either all mathematicians or only those in somewhat related fields has long been felt, but little has been done outside of the USSR. The serial publication ''Advances in Mathematics'' was created in response to this demand." Abstracting and indexing The journal is abstracted and indexed in: * [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Factor Complex
In mathematics, the free factor complex (sometimes also called the complex of free factors) is a free group counterpart of the notion of the curve complex of a finite type surface. The free factor complex was originally introduced in a 1998 paper of Allen Hatcher and Karen Vogtmann. Like the curve complex, the free factor complex is known to be Gromov-hyperbolic. The free factor complex plays a significant role in the study of large-scale geometry of \operatorname(F_n). Formal definition For a free group G a ''proper free factor'' of G is a subgroup A\le G such that A\ne \, A\ne G and that there exists a subgroup B\le G such that G=A\ast B. Let n\ge 3 be an integer and let F_n be the free group of rank n. The free factor complex \mathcal F_n for F_n is a simplicial complex where: (1) The 0-cells are the conjugacy classes in F_n of proper free factors of F_n, that is :\mathcal F_n^=\. (2) For k\ge 1, a k-simplex in \mathcal F_n is a collection of k+1 distinct 0-cells \\su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Groups, Geometry, And Dynamics
''Groups, Geometry, and Dynamics'' is a quarterly peer-reviewed mathematics journal published quarterly by the European Mathematical Society. It was established in 2007 and covers all aspects of groups, group actions, geometry and dynamical systems. The journal is indexed by ''Mathematical Reviews'' and Zentralblatt MATH. Its 2009 MCQ was 0.65, and its 2012 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as i ... is 0.867. External links * Mathematics journals Academic journals established in 2007 English-language journals European Mathematical Society academic journals Quarterly journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tits Alternative
In mathematics, the Tits alternative, named for Jacques Tits, is an important theorem about the structure of finitely generated linear groups. Statement The theorem, proven by Tits, is stated as follows. Consequences A linear group is not amenable if and only if it contains a non-abelian free group (thus the von Neumann conjecture, while not true in general, holds for linear groups). The Tits alternative is an important ingredient in the proof of Gromov's theorem on groups of polynomial growth. In fact the alternative essentially establishes the result for linear groups (it reduces it to the case of solvable groups, which can be dealt with by elementary means). Generalizations In geometric group theory, a group ''G'' is said to satisfy the Tits alternative if for every subgroup ''H'' of ''G'' either ''H'' is virtually solvable or ''H'' contains a nonabelian free subgroup (in some versions of the definition this condition is only required to be satisfied for all finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric And Functional Analysis (journal)
''Geometric and Functional Analysis'' (''GAFA'') is a mathematical journal published by Birkhäuser, an independent division of Springer-Verlag. The journal is published approximately bi-monthly. The journal publishes papers on broad range of topics in geometry and analysis including geometric analysis, riemannian geometry, symplectic geometry, geometric group theory, non-commutative geometry, automorphic forms and analytic number theory, and others. ''GAFA'' is both an acronym and a part of the official full name of the journal. History ''GAFA'' was founded in 1991 by Mikhail Gromov and Vitali Milman. The idea for the journal was inspired by the long-running Israeli seminar series "Geometric Aspects of Functional Analysis" of which Vitali Milman had been one of the main organizers in the previous years. The journal retained the same acronym as the series to stress the connection between the two. Journal information The journal is reviewed cover-to-cover in Mathematical Revie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normalizer
In mathematics, especially group theory, the centralizer (also called commutant) of a subset ''S'' in a group ''G'' is the set of elements \mathrm_G(S) of ''G'' such that each member g \in \mathrm_G(S) commutes with each element of ''S'', or equivalently, such that conjugation by g leaves each element of ''S'' fixed. The normalizer of ''S'' in ''G'' is the set of elements \mathrm_G(S) of ''G'' that satisfy the weaker condition of leaving the set S \subseteq G fixed under conjugation. The centralizer and normalizer of ''S'' are subgroups of ''G''. Many techniques in group theory are based on studying the centralizers and normalizers of suitable subsets ''S''. Suitably formulated, the definitions also apply to semigroups. In ring theory, the centralizer of a subset of a ring is defined with respect to the semigroup (multiplication) operation of the ring. The centralizer of a subset of a ring ''R'' is a subring of ''R''. This article also deals with centralizers and no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
