|
Frequency-domain Beamformer
In physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency, rather than time. Put simply, a time-domain graph shows how a signal changes over time, whereas a frequency-domain graph shows how much of the signal lies within each given frequency band over a range of frequencies. A frequency-domain representation can also include information on the phase shift that must be applied to each sinusoid in order to be able to recombine the frequency components to recover the original time signal. A given function or signal can be converted between the time and frequency domains with a pair of mathematical operators called transforms. An example is the Fourier transform, which converts a time function into a complex valued sum or integral of sine waves of different frequencies, with amplitudes and phases, each of which represents a frequency component. The " spect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform Time And Frequency Domains (small)
Fourier may refer to: People named Fourier *Joseph Fourier (1768–1830), French mathematician and physicist *Charles Fourier (1772–1837), French utopian socialist thinker *Peter Fourier (1565–1640), French saint in the Roman Catholic Church and priest of Mattaincourt Mathematics *Fourier series, a weighted sum of sinusoids having a common period, the result of Fourier analysis of a periodic function * Fourier analysis, the description of functions as sums of sinusoids *Fourier transform, the type of linear canonical transform that is the generalization of the Fourier series *Fourier operator, the kernel of the Fredholm integral of the first kind that defines the continuous Fourier transform * Fourier inversion theorem, any one of several theorems by which Fourier inversion recovers a function from its Fourier transform *Short-time Fourier transform or short-term Fourier transform (STFT), a Fourier transform during a short term of time, used in the area of signal analysis * Fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Fourier Transform
In mathematics, the Fourier inversion theorem says that for many types of functions it is possible to recover a function from its Fourier transform. Intuitively it may be viewed as the statement that if we know all frequency and phase information about a wave then we may reconstruct the original wave precisely. The theorem says that if we have a function f:\R \to \Complex satisfying certain conditions, and we use the convention for the Fourier transform that :(\mathcalf)(\xi):=\int_ e^ \, f(y)\,dy, then :f(x)=\int_ e^ \, (\mathcalf)(\xi)\,d\xi. In other words, the theorem says that :f(x)=\iint_ e^ \, f(y)\,dy\,d\xi. This last equation is called the Fourier integral theorem. Another way to state the theorem is that if R is the flip operator i.e. (Rf)(x) := f(-x), then :\mathcal^=\mathcalR=R\mathcal. The theorem holds if both f and its Fourier transform are absolutely integrable (in the Lebesgue sense) and f is continuous at the point x. However, even under more general ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
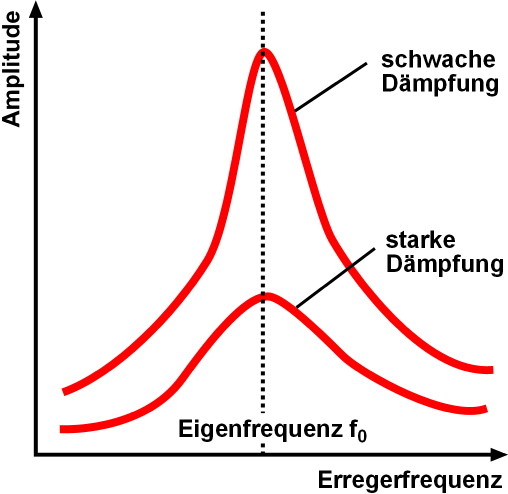
Resonance Width
In physics and engineering, the quality factor or ''Q'' factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation. Q factor is alternatively defined as the ratio of a resonator's centre frequency to its bandwidth when subject to an oscillating driving force. These two definitions give numerically similar, but not identical, results. Higher ''Q'' indicates a lower rate of energy loss and the oscillations die out more slowly. A pendulum suspended from a high-quality bearing, oscillating in air, has a high ''Q'', while a pendulum immersed in oil has a low one. Resonators with high quality factors have low damping, so that they ring or vibrate longer. Explanation The Q factor is a parameter that describes the resonance behavior of an underdamped harmonic oscillator (resonator). Sinusoidally driven resonators h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Constant
In physics and engineering, the time constant, usually denoted by the Greek letter (tau), is the parameter characterizing the response to a step input of a first-order, linear time-invariant (LTI) system.Concretely, a first-order LTI system is a system that can be modeled by a single first order differential equation in time. Examples include the simplest single-stage electrical RC circuits and RL circuits. The time constant is the main characteristic unit of a first-order LTI system. In the time domain, the usual choice to explore the time response is through the step response to a step input, or the impulse response to a Dirac delta function input. In the frequency domain (for example, looking at the Fourier transform of the step response, or using an input that is a simple sinusoidal function of time) the time constant also determines the bandwidth of a first-order time-invariant system, that is, the frequency at which the output signal power drops to half the value it has at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resonant Frequency
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) and reson ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gain (electronics)
In electronics, gain is a measure of the ability of a two-port electrical network, circuit (often an amplifier) to increase the Electric power, power or amplitude of a Signal (electrical engineering), signal from the input to the output port by adding energy converted from some power supply to the signal. It is usually defined as the mean ratio of the Signalling (telecommunication), signal amplitude or power at the output port (circuit theory), port to the amplitude or power at the input port. It is often expressed using the logarithmic decibel (dB) units ("dB gain"). A gain greater than one (greater than zero dB), that is amplification, is the defining property of an active component or circuit, while a passive circuit will have a gain of less than one. The term ''gain'' alone is ambiguous, and can refer to the ratio of output to input voltage (''voltage gain''), Electric current, current (''current gain'') or electric power (''power gain''). In the field of audio and general ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Response
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of systems, such as audio and control systems, where they simplify mathematical analysis by converting governing differential equations into algebraic equations. In an audio system, it may be used to minimize audible distortion by designing components (such as microphones, amplifiers and loudspeakers) so that the overall response is as flat (uniform) as possible across the system's bandwidth. In control systems, such as a vehicle's cruise control, it may be used to assess system stability, often through the use of Bode plots. Systems with a specific frequency response can be designed using analog and digital filters. The frequency response characterizes systems in the frequency domain, just as the impulse response characterizes systems in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bandwidth (signal Processing)
Bandwidth is the difference between the upper and lower frequencies in a continuous band of frequencies. It is typically measured in hertz, and depending on context, may specifically refer to ''passband bandwidth'' or ''baseband bandwidth''. Passband bandwidth is the difference between the upper and lower cutoff frequencies of, for example, a band-pass filter, a communication channel, or a signal spectrum. Baseband bandwidth applies to a low-pass filter or baseband signal; the bandwidth is equal to its upper cutoff frequency. Bandwidth in hertz is a central concept in many fields, including electronics, information theory, digital communications, radio communications, signal processing, and spectroscopy and is one of the determinants of the capacity of a given communication channel. A key characteristic of bandwidth is that any band of a given width can carry the same amount of information, regardless of where that band is located in the frequency spectrum. For example, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form :P = 0 where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equation'' refers only to ''univariate equations'', that is polynomial equations that involve only one variable. On the other hand, a polynomial equation may involve several variables. In the case of several variables (the ''multivariate'' case), the term ''polynomial equation'' is usually preferred to ''algebraic equation''. For example, :x^5-3x+1=0 is an algebraic equation with integer coefficients and :y^4 + \frac - \frac + xy^2 + y^2 + \frac = 0 is a multivariate polynomial equation over the rationals. Some but not all polynomial equations with rational coefficients have a solution that is an algebraic expression that can be found using a finite number of operations that involve only those same types of coefficients (that is, can be solved alg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Differential Equation
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y + a_1(x)y' + a_2(x)y'' \cdots + a_n(x)y^ = b(x) where and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of an unknown function of the variable . Such an equation is an ordinary differential equation (ODE). A ''linear differential equation'' may also be a linear partial differential equation (PDE), if the unknown function depends on several variables, and the derivatives that appear in the equation are partial derivatives. A linear differential equation or a system of linear equations such that the associated homogeneous equations have constant coefficients may be solved by quadrature, which means that the solutions may be expressed in terms of integrals. This is also true for a linear equation of order one, with non-con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
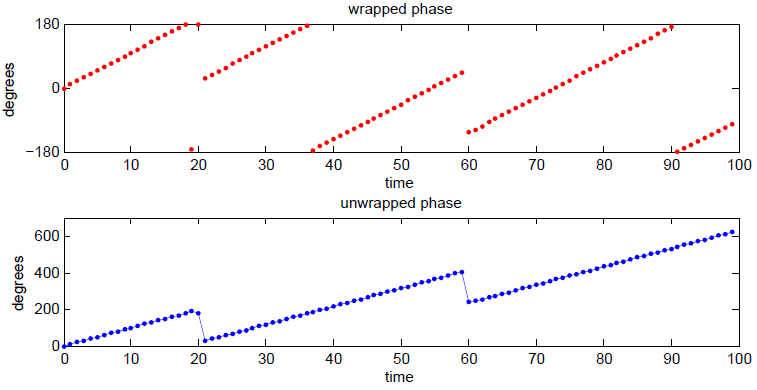
Instantaneous Frequency
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''complex-valued'' function ''s''(''t''), is the real-valued function: :\varphi(t) = \arg\, where arg is the complex argument function. The instantaneous frequency is the temporal rate of change of the instantaneous phase. And for a ''real-valued'' function ''s''(''t''), it is determined from the function's analytic representation, ''s''a(''t''): :\begin \varphi(t) &= \arg\ \\ pt &= \arg\, \end where \hat(t) represents the Hilbert transform of ''s''(''t''). When ''φ''(''t'') is constrained to its principal value, either the interval or , it is called ''wrapped phase''. Otherwise it is called ''unwrapped phase'', which is a continuous function of argument ''t'', assuming ''s''a(''t'') is a continuous function of ''t''. Unless o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.gif)