|
Free Magma
In abstract algebra, a magma, binar, or, rarely, groupoid is a basic kind of algebraic structure. Specifically, a magma consists of a set equipped with a single binary operation that must be closed by definition. No other properties are imposed. History and terminology The term ''groupoid'' was introduced in 1927 by Heinrich Brandt describing his Brandt groupoid (translated from the German ). The term was then appropriated by B. A. Hausmann and Øystein Ore (1937) in the sense (of a set with a binary operation) used in this article. In a couple of reviews of subsequent papers in Zentralblatt, Brandt strongly disagreed with this overloading of terminology. The Brandt groupoid is a groupoid in the sense used in category theory, but not in the sense used by Hausmann and Ore. Nevertheless, influential books in semigroup theory, including Clifford and Preston (1961) and Howie (1995) use groupoid in the sense of Hausmann and Ore. Hollings (2014) writes that the term ''groupoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures. Algebraic structures include groups, rings, fields, modules, vector spaces, lattices, and algebras over a field. The term ''abstract algebra'' was coined in the early 20th century to distinguish this area of study from older parts of algebra, and more specifically from elementary algebra, the use of variables to represent numbers in computation and reasoning. Algebraic structures, with their associated homomorphisms, form mathematical categories. Category theory is a formalism that allows a unified way for expressing properties and constructions that are similar for various structures. Universal algebra is a related subject that studies types of algebraic structures as single objects. For example, the structure of groups is a single object in universal algebra, which is called the '' variety of groups''. History Before the nineteenth century, alge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Element (mathematics)
In mathematics, an element (or member) of a set is any one of the distinct objects that belong to that set. Sets Writing A = \ means that the elements of the set are the numbers 1, 2, 3 and 4. Sets of elements of , for example \, are subsets of . Sets can themselves be elements. For example, consider the set B = \. The elements of are ''not'' 1, 2, 3, and 4. Rather, there are only three elements of , namely the numbers 1 and 2, and the set \. The elements of a set can be anything. For example, C = \ is the set whose elements are the colors , and . Notation and terminology The relation "is an element of", also called set membership, is denoted by the symbol "∈". Writing :x \in A means that "''x'' is an element of ''A''". Equivalent expressions are "''x'' is a member of ''A''", "''x'' belongs to ''A''", "''x'' is in ''A''" and "''x'' lies in ''A''". The expressions "''A'' includes ''x''" and "''A'' contains ''x''" are also used to m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. Informally, a free object over a set ''A'' can be thought of as being a "generic" algebraic structure over ''A'': the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure. Examples include free groups, tensor algebras, or free lattices. The concept is a part of universal algebra, in the sense that it relates to all types of algebraic structure (with finitary operations). It also has a formulation in terms of category theory, although this is in yet more abstract terms. Definition Free objects are the direct generalization to categories of the notion of basis in a vector space. A linear function between vector spaces is entirely determined by its values on a basis of the vector space The following definition translates this to any category. A concrete category is a category that is equipped with a f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiisomorphic
In category theory, a branch of mathematics, an antiisomorphism (or anti-isomorphism) between structured sets ''A'' and ''B'' is an isomorphism from ''A'' to the opposite of ''B'' (or equivalently from the opposite of ''A'' to ''B''). If there exists an antiisomorphism between two structures, they are said to be ''antiisomorphic.'' Intuitively, to say that two mathematical structures are ''antiisomorphic'' is to say that they are basically opposites of one another. The concept is particularly useful in an algebraic setting, as, for instance, when applied to rings. Simple example Let ''A'' be the binary relation (or directed graph) consisting of elements and binary relation \rightarrow defined as follows: * 1 \rightarrow 2, * 1 \rightarrow 3, * 2 \rightarrow 1. Let ''B'' be the binary relation set consisting of elements and binary relation \Rightarrow defined as follows: * b \Rightarrow a, * c \Rightarrow a, * a \Rightarrow b. Note that the opposite of ''B'' (denoted ''B' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσος ''isos'' "equal", and μορφή ''morphe'' "form" or "shape". The interest in isomorphisms lies in the fact that two isomorphic objects have the same properties (excluding further information such as additional structure or names of objects). Thus isomorphic structures cannot be distinguished from the point of view of structure only, and may be identified. In mathematical jargon, one says that two objects are . An automorphism is an isomorphism from a structure to itself. An isomorphism between two structures is a canonical isomorphism (a canonical map that is an isomorphism) if there is only one isomorphism between the two structures (as it is the case for solutions of a univer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan Number
In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles Catalan (1814–1894). The ''n''th Catalan number can be expressed directly in terms of binomial coefficients by :C_n = \frac = \frac = \prod\limits_^\frac \qquad\textn\ge 0. The first Catalan numbers for ''n'' = 0, 1, 2, 3, ... are :1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ... . Properties An alternative expression for ''C''''n'' is :C_n = - for n\ge 0, which is equivalent to the expression given above because \tbinom=\tfrac\tbinomn. This expression shows that ''C''''n'' is an integer, which is not immediately obvious from the first formula given. This expression forms the basis for a proof of the correctness of the formula. The Catalan numbers satisfy the recurrence relations :C_0 = 1 \quad \text \quad C_=\sum_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dyck Language
In the theory of formal languages of computer science, mathematics, and linguistics, a Dyck word is a balanced string of square brackets and The set of Dyck words forms the Dyck language. Dyck words and language are named after the mathematician Walther von Dyck. They have applications in the parsing of expressions that must have a correctly nested sequence of brackets, such as arithmetic or algebraic expressions. Formal definition Let \Sigma = \ be the alphabet consisting of the symbols and Let \Sigma^ denote its Kleene closure. The Dyck language is defined as: : \. Context-free grammar It may be helpful to define the Dyck language via a context-free grammar in some situations. The Dyck language is generated by the context-free grammar with a single non-terminal , and the production: : That is, ''S'' is either the empty string () or is " , an element of the Dyck language, the matching ", and an element of the Dyck language. An alternative context-free grammar for th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
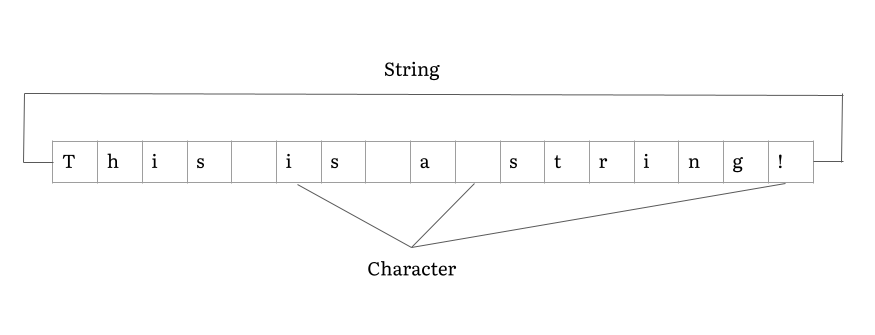
String (computer Science)
In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed (after creation). A string is generally considered as a data type and is often implemented as an array data structure of bytes (or words) that stores a sequence of elements, typically characters, using some character encoding. ''String'' may also denote more general arrays or other sequence (or list) data types and structures. Depending on the programming language and precise data type used, a variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears literally in source code, it is known as a string literal or an anonymous string. In formal languages, which are used in mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Currying
In mathematics and computer science, currying is the technique of translating the evaluation of a function that takes multiple arguments into evaluating a sequence of functions, each with a single argument. For example, currying a function f that takes three arguments creates a nested unary function g, so that the code :\textx=f(a,b,c) gives x the same value as the code : \begin \texth = g(a) \\ \texti = h(b) \\ \textx = i(c), \end or called in sequence, :\textx = g(a)(b)(c). In a more mathematical language, a function that takes two arguments, one from X and one from Y, and produces outputs in Z, by currying is translated into a function that takes a single argument from X and produces as outputs ''functions'' from Y to Z. This is a natural one-to-one correspondence between these two types of functions, so that the sets together with functions between them form a Cartesian closed category. The currying of a function with more than two arguments can then be defined by induction. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reverse Polish Notation
Reverse Polish notation (RPN), also known as reverse Łukasiewicz notation, Polish postfix notation or simply postfix notation, is a mathematical notation in which operators ''follow'' their operands, in contrast to Polish notation (PN), in which operators ''precede'' their operands. It does not need any parentheses as long as each operator has a fixed number of operands. The description "Polish" refers to the nationality of logician Jan Łukasiewicz, who invented Polish notation in 1924. The first computer to use postfix notation, though it long remained essentially unknown outside of Germany, was Konrad Zuse's Z3 in 1941 as well as his Z4 in 1945. The reverse Polish scheme was again proposed in 1954 by Arthur Burks, Don Warren, and Jesse Wright and was independently reinvented by Friedrich L. Bauer and Edsger W. Dijkstra in the early 1960s to reduce computer memory access and use the stack to evaluate expressions. The algorithms and notation for this scheme were extended b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Postfix Notation
Reverse Polish notation (RPN), also known as reverse Łukasiewicz notation, Polish postfix notation or simply postfix notation, is a mathematical notation in which operators ''follow'' their operands, in contrast to Polish notation (PN), in which operators ''precede'' their operands. It does not need any parentheses as long as each operator has a fixed number of operands. The description "Polish" refers to the nationality of logician Jan Łukasiewicz, who invented Polish notation in 1924. The first computer to use postfix notation, though it long remained essentially unknown outside of Germany, was Konrad Zuse's Z3 in 1941 as well as his Z4 in 1945. The reverse Polish scheme was again proposed in 1954 by Arthur Burks, Don Warren, and Jesse Wright and was independently reinvented by Friedrich L. Bauer and Edsger W. Dijkstra in the early 1960s to reduce computer memory access and use the stack to evaluate expressions. The algorithms and notation for this scheme were extend ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prefix Notation
Polish notation (PN), also known as normal Polish notation (NPN), Łukasiewicz notation, Warsaw notation, Polish prefix notation or simply prefix notation, is a mathematical notation in which operators ''precede'' their operands, in contrast to the more common infix notation, in which operators are placed ''between'' operands, as well as reverse Polish notation (RPN), in which operators ''follow'' their operands. It does not need any parentheses as long as each operator has a fixed number of operands. The description "Polish" refers to the nationality of logician Jan Łukasiewicz, who invented Polish notation in 1924. The term ''Polish notation'' is sometimes taken (as the opposite of ''infix notation'') to also include reverse Polish notation. When Polish notation is used as a syntax for mathematical expressions by programming language interpreters, it is readily parsed into abstract syntax trees and can, in fact, define a one-to-one representation for the same. Because o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |