|
Fractional Matching
In graph theory, a fractional matching is a generalization of a matching in which, intuitively, each vertex may be broken into fractions that are matched to different neighbor vertices. Definition Given a graph G=(V,E), a fractional matching in G is a function that assigns, to each edge e\in E, a fraction f(e)\in ,1/math>, such that for every vertex v\in V, the sum of fractions of edges adjacent to v is at most one: \forall v\in V: \sum_f(e)\leq 1 A matching in the traditional sense is a special case of a fractional matching, in which the fraction of every edge is either zero or one: f(e)=1 if e is in the matching, and f(e)=0 if it is not. For this reason, in the context of fractional matchings, usual matchings are sometimes called ''integral matchings''. Size The size of an integral matching is the number of edges in the matching, and the matching number \nu(G) of a graph G is the largest size of a matching in G. Analogously, the ''size'' of a fractional matching is the sum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph Theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') which are connected by ''Glossary of graph theory terms#edge, edges'' (also called ''arcs'', ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a Set (mathematics), set of vertices (also called nodes or points); * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Birkhoff's Algorithm
Birkhoff's algorithm (also called Birkhoff-von-Neumann algorithm) is an algorithm for decomposing a bistochastic matrix into a convex combination of permutation matrices. It was published by Garrett Birkhoff in 1946. It has many applications. One such application is for the problem of fair random assignment: given a randomized allocation of items, Birkhoff's algorithm can decompose it into a lottery on deterministic allocations. Terminology A ''bistochastic matrix'' (also called: ''doubly-stochastic'') is a matrix in which all elements are greater than or equal to 0 and the sum of the elements in each row and column equals 1. An example is the following 3-by-3 matrix: \begin 0.2 & 0.3 & 0.5 \\ 0.6 & 0.2 & 0.2 \\ 0.2 & 0.5 & 0.3 \end A ''permutation matrix'' is a special case of a bistochastic matrix, in which each element is either 0 or 1 (so there is exactly one "1" in each row and each column). An example is the following 3-by-3 matrix: \begin 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Convex Hull
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a Bounded set, bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its projective duality, dual problem of intersecting Half-space (geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Matching Polytope
In graph theory, the matching polytope of a given graph is a geometric object representing the possible matchings in the graph. It is a convex polytope each of whose corners corresponds to a matching. It has great theoretical importance in the theory of matching. Preliminaries Incidence vectors and matrices Let ''G'' = (''V'', ''E'') be a graph with ''n'' = , ''V'', nodes and ''m'' = , ''E'', edges. For every subset ''U'' of vertices, its ''incidence vector'' 1''U'' is a vector of size ''n'', in which element ''v'' is 1 if node v is in ''U'', and 0 otherwise. Similarly, for every subset ''F'' of edges, its incidence vector 1F is a vector of size ''m'', in which element ''e'' is 1 if edge ''e'' is in ''F,'' and 0 otherwise. For every node ''v'' in ''V'', the set of edges in ''E'' adjacent to ''v'' is denoted by ''E''(''v''). Therefore, each vector 1''E(v)'' is a 1-by-''m'' vector in which element ''e'' is 1 if edge ''e'' is adjacent to ''v,'' and 0 otherwise. The ''incide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Convex Polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> (including this article) allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary. Convex polytopes play an important role both in various branches of mathematics and in applied areas, most notably in linear programming. In the influential textbooks of Grünbaum and Ziegler on the subject, as well as in many other texts in discrete geometry, convex polytopes are often simply called "polytopes". Grünbaum points out that this is solely to avoid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Augmenting Path
In graph theory, a flow network (also known as a transportation network) is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in operations research, a directed graph is called a network, the vertices are called nodes and the edges are called arcs. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, unless it is a source, which has only outgoing flow, or sink, which has only incoming flow. A flow network can be used to model traffic in a computer network, circulation with demands, fluids in pipes, currents in an electrical circuit, or anything similar in which something travels through a network of nodes. As such, efficient algorithms for solving network flows can also be applied to solve problems that can be reduced to a flow network, including survey design, airline scheduling, image segmentation, and the Matching (graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
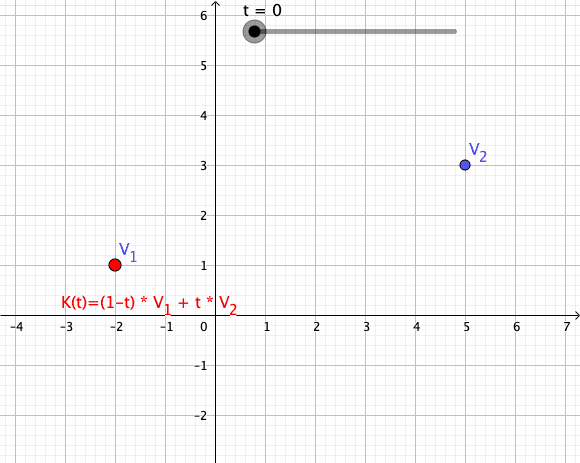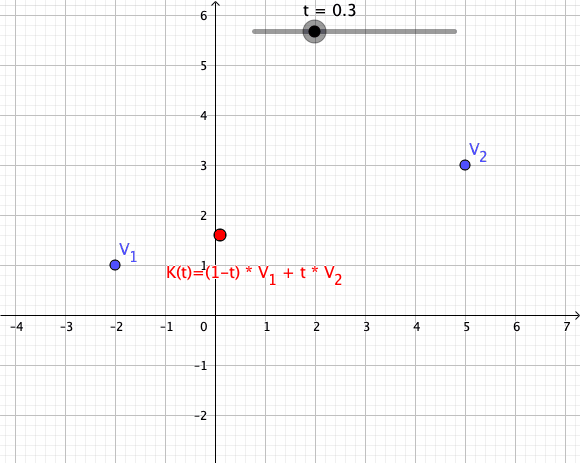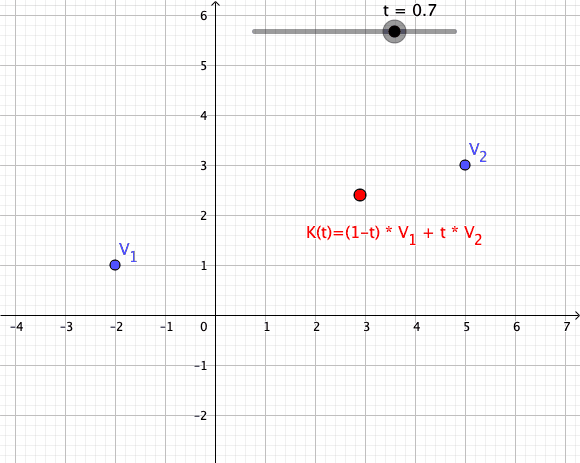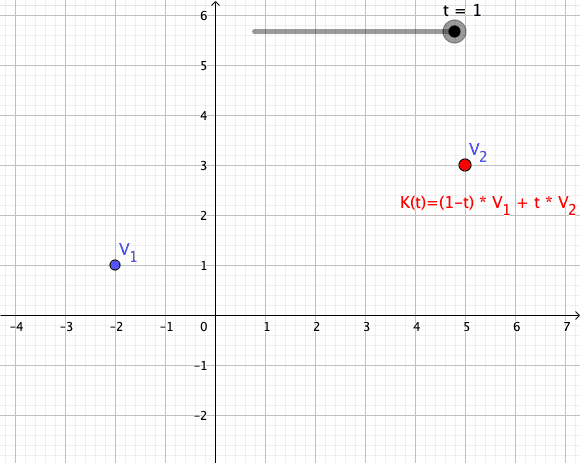
Convex Combination
In convex geometry and Vector space, vector algebra, a convex combination is a linear combination of point (geometry), points (which can be vector (geometric), vectors, scalar (mathematics), scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. Formal definition More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form : \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex set, convex if it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Doubly Stochastic Matrix
In mathematics, especially in probability and combinatorics, a doubly stochastic matrix (also called bistochastic matrix) is a square matrix X=(x_) of nonnegative real numbers, each of whose rows and columns sums to 1, i.e., :\sum_i x_=\sum_j x_=1, Thus, a doubly stochastic matrix is both left stochastic and right stochastic. Indeed, any matrix that is both left and right stochastic must be square: if every row sums to 1 then the sum of all entries in the matrix must be equal to the number of rows, and since the same holds for columns, the number of rows and columns must be equal. Birkhoff polytope The class of n\times n doubly stochastic matrices is a convex polytope known as the Birkhoff polytope B_n. Using the matrix entries as Cartesian coordinates, it lies in an (n-1)^2-dimensional affine subspace of n^2-dimensional Euclidean space defined by 2n-1 independent linear constraints specifying that the row and column sums all equal 1. (There are 2n-1 constraints rather than 2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Matching (graph Theory)
In the mathematical discipline of graph theory, a matching or independent edge set in an undirected Graph (discrete mathematics), graph is a set of Edge (graph theory), edges without common vertex (graph theory), vertices. In other words, a subset of the edges is a matching if each vertex appears in at most one edge of that matching. Finding a matching in a bipartite graph can be treated as a Flow network, network flow problem. Definitions Given a Graph (discrete mathematics), graph a matching ''M'' in ''G'' is a set of pairwise non-adjacent edges, none of which are loop (graph theory), loops; that is, no two edges share common vertices. A vertex is matched (or saturated) if it is an endpoint of one of the edges in the matching. Otherwise the vertex is unmatched (or unsaturated). A maximal matching is a matching ''M'' of a graph ''G'' that is not a subset of any other matching. A matching ''M'' of a graph ''G'' is maximal if every edge in ''G'' has a non-empty intersectio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Maximum Flow Problem
In Optimization (mathematics), optimization theory, maximum flow problems involve finding a feasible flow through a flow network that obtains the maximum possible flow rate. The maximum flow problem can be seen as a special case of more complex network flow problems, such as the circulation problem. The maximum value of an s-t flow (i.e., flow from Glossary of graph theory#Direction, source s to Glossary of graph theory#Direction, sink t) is equal to the minimum capacity of an Cut (graph theory), s-t cut (i.e., cut severing s from t) in the network, as stated in the max-flow min-cut theorem. History The maximum flow problem was first formulated in 1954 by Ted Harris (mathematician), T. E. Harris and F. S. Ross as a simplified model of Soviet railway traffic flow. In 1955, Lester R. Ford, Jr. and D. R. Fulkerson, Delbert R. Fulkerson created the first known algorithm, the Ford–Fulkerson algorithm.Ford, L.R., Jr.; Fulkerson, D.R., ''Flows in Networks'', Princeton University Press ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear function#As a polynomial function, linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the mathematical optimization, optimization of a linear objective function, subject to linear equality and linear inequality Constraint (mathematics), constraints. Its feasible region is a convex polytope, which is a set defined as the intersection (mathematics), intersection of finitely many Half-space (geometry), half spaces, each of which is defined by a linear inequality. Its objective function is a real number, real-valued affine function, affine (linear) function defined on this polytope. A linear programming algorithm finds a point in the po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |