|
Formal Verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property, using formal methods of mathematics. Formal verification is a key incentive for formal specification of systems, and is at the core of formal methods. It represents an important dimension of analysis and verification in electronic design automation and is one approach to software verification. The use of formal verification enables the highest Evaluation Assurance Level ( EAL7) in the framework of common criteria for computer security certification. Formal verification can be helpful in proving the correctness of systems such as: cryptographic protocols, combinational circuits, digital circuits with internal memory, and software expressed as source code in a programming language. Prominent examples of verified software systems include the CompCert verified C compiler and the seL ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Hardware
Computer hardware includes the physical parts of a computer, such as the central processing unit (CPU), random-access memory (RAM), motherboard, computer data storage, graphics card, sound card, and computer case. It includes external devices such as a Computer monitor, monitor, Computer mouse, mouse, Computer keyboard, keyboard, and Computer speakers, speakers. By contrast, software is a set of written instructions that can be stored and run by hardware. Hardware derived its name from the fact it is ''Hardness, hard'' or rigid with respect to changes, whereas software is ''soft'' because it is easy to change. Hardware is typically directed by the software to execute any command or Instruction (computing), instruction. A combination of hardware and software forms a usable computing system, although Digital electronics, other systems exist with only hardware. History Early computing devices were more complicated than the ancient abacus date to the seventeenth century. French ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Source Code
In computing, source code, or simply code or source, is a plain text computer program written in a programming language. A programmer writes the human readable source code to control the behavior of a computer. Since a computer, at base, only understands machine code, source code must be Translator (computing), translated before a computer can Execution (computing), execute it. The translation process can be implemented three ways. Source code can be converted into machine code by a compiler or an assembler (computing), assembler. The resulting executable is machine code ready for the computer. Alternatively, source code can be executed without conversion via an interpreter (computing), interpreter. An interpreter loads the source code into memory. It simultaneously translates and executes each statement (computer science), statement. A method that combines compilation and interpretation is to first produce bytecode. Bytecode is an intermediate representation of source code tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
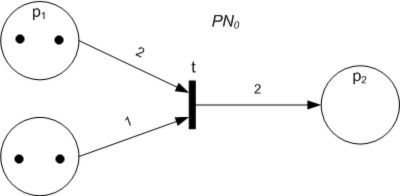
Vector Addition System
A vector addition system (VAS) is one of several mathematical modeling languages for the description of distributed systems. Vector addition systems were introduced by Richard M. Karp and Raymond E. Miller in 1969, and generalized to vector addition systems with states (VASS) by John Hopcroft, John E. Hopcroft and Jean-Jacques Pansiot in 1979. Both VAS and VASS are equivalent in many ways to Petri nets introduced earlier by Carl Adam Petri. Reachability problem, Reachability in vector addition systems is Ackermann function , Ackermann-complete (and hence nonelementary problem , nonelementary). Informal definition A ''vector addition system'' consists of a finite set of integer row vector, vectors with all vectors having the same length. An initial vector is seen as the initial values of multiple counters, and the vectors of the VAS are seen as updates. These counters may never drop below zero. More precisely, given an initial vector with non negative values, the vectors of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Petri Net
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Pet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Horn Clause
In mathematical logic and logic programming, a Horn clause is a logical formula of a particular rule-like form that gives it useful properties for use in logic programming, formal specification, universal algebra and model theory. Horn clauses are named for the logician Alfred Horn, who first pointed out their significance in 1951. Definition A Horn clause is a disjunctive clause (a disjunction of literals) with at most one positive, i.e. unnegated, literal. Conversely, a disjunction of literals with at most one negated literal is called a dual-Horn clause. A Horn clause with exactly one positive literal is a definite clause or a strict Horn clause; a definite clause with no negative literals is a unit clause, and a unit clause without variables is a fact; a Horn clause without a positive literal is a goal clause. The empty clause, consisting of no literals (which is equivalent to ''false''), is a goal clause. These three kinds of Horn clauses are illustrated in the follo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Labelled Transition System
In theoretical computer science, a transition system is a concept used in the study of computation. It is used to describe the potential behavior of discrete systems. It consists of states and transitions between states, which may be labeled with labels chosen from a set; the same label may appear on more than one transition. If the label set is a singleton, the system is essentially unlabeled, and a simpler definition that omits the labels is possible. Transition systems coincide mathematically with abstract rewriting systems (as explained further in this article) and directed graphs. They differ from finite-state automata in several ways: * The set of states is not necessarily finite, or even countable. * The set of transitions is not necessarily finite, or even countable. * No "start" state or "final" states are given. Transition systems can be represented as directed graphs. Formal definition Formally, a transition system is a pair (S, T) where S is a set of states ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Finite-state Machine
A finite-state machine (FSM) or finite-state automaton (FSA, plural: ''automata''), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of ''State (computer science), states'' at any given time. The FSM can change from one state to another in response to some Input (computer science), inputs; the change from one state to another is called a ''transition''. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—Deterministic finite automaton, deterministic finite-state machines and Nondeterministic finite automaton, non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed. The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematical Model
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathematics and in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right. The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Formal Proof
In logic and mathematics, a formal proof or derivation is a finite sequence of sentences (known as well-formed formulas when relating to formal language), each of which is an axiom, an assumption, or follows from the preceding sentences in the sequence, according to the rule of inference. It differs from a natural language argument in that it is rigorous, unambiguous and mechanically verifiable. If the set of assumptions is empty, then the last sentence in a formal proof is called a theorem of the formal system. The notion of theorem is generally effective, but there may be no method by which we can reliably find proof of a given sentence or determine that none exists. The concepts of Fitch-style proof, sequent calculus and natural deduction are generalizations of the concept of proof. The theorem is a syntactic consequence of all the well-formed formulas preceding it in the proof. For a well-formed formula to qualify as part of a proof, it must be the result of applying a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kernel (operating System)
A kernel is a computer program at the core of a computer's operating system that always has complete control over everything in the system. The kernel is also responsible for preventing and mitigating conflicts between different processes. It is the portion of the operating system code that is always resident in memory and facilitates interactions between hardware and software components. A full kernel controls all hardware resources (e.g. I/O, memory, cryptography) via device drivers, arbitrates conflicts between processes concerning such resources, and optimizes the use of common resources, such as CPU, cache, file systems, and network sockets. On most systems, the kernel is one of the first programs loaded on startup (after the bootloader). It handles the rest of startup as well as memory, peripherals, and input/output (I/O) requests from software, translating them into data-processing instructions for the central processing unit. The critical code of the kernel is usua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
SeL4
L4 is a family of second-generation microkernels, used to implement a variety of types of operating systems (OS), though mostly for Unix-like, ''Portable Operating System Interface'' (POSIX) compliant types. L4, like its predecessor microkernel L3, was created by German computer scientist Jochen Liedtke as a response to the poor performance of earlier microkernel-based OSes. Liedtke felt that a system designed from the start for high performance, rather than other goals, could produce a microkernel of practical use. His original implementation in hand-coded Intel i386-specific assembly language code in 1993 created attention by being 20 times faster than Mach. The follow-up publication two years later was considered so influential that it won the 2015 ACM SIGOPS Hall of Fame Award. Since its introduction, L4 has been developed to be cross-platform and to improve security, isolation, and robustness. There have been various re-implementations of the original L4 kernel application ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Compiler
In computing, a compiler is a computer program that Translator (computing), translates computer code written in one programming language (the ''source'' language) into another language (the ''target'' language). The name "compiler" is primarily used for programs that translate source code from a high-level programming language to a lower level language, low-level programming language (e.g. assembly language, object code, or machine code) to create an executable program.Compilers: Principles, Techniques, and Tools by Alfred V. Aho, Ravi Sethi, Jeffrey D. Ullman - Second Edition, 2007 There are many different types of compilers which produce output in different useful forms. A ''cross-compiler'' produces code for a different Central processing unit, CPU or operating system than the one on which the cross-compiler itself runs. A ''bootstrap compiler'' is often a temporary compiler, used for compiling a more permanent or better optimised compiler for a language. Related software ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |