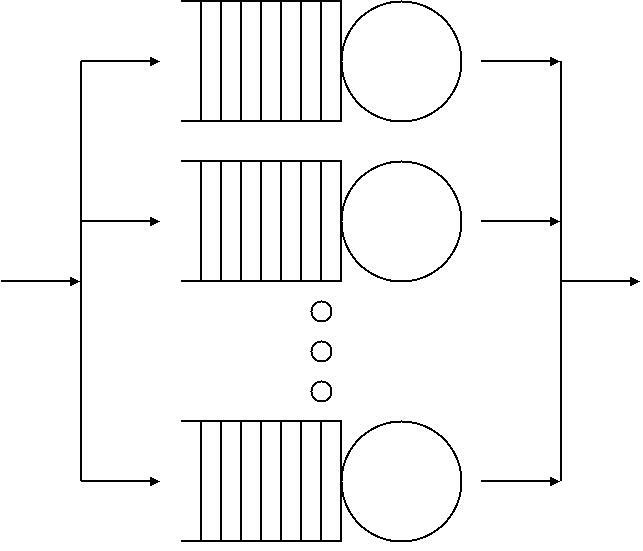
|
First-come, First-served
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. Queueing theory has its origins in research by Agner Krarup Erlang when he created models to describe the system of Copenhagen Telephone Exchange company, a Danish company. The ideas have since seen applications including telecommunication, traffic engineering, computing and, particularly in industrial engineering, in the design of factories, shops, offices and hospitals, as well as in project management. Spelling The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is ''Queueing Systems''. Single queueing nodes A queue, or queueing node ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Balance Equation
In probability theory, a balance equation is an equation that describes the probability flux associated with a Markov chain in and out of states or set of states. Global balance The global balance equations (also known as full balance equations) are a set of equations that characterize the equilibrium distribution (or any stationary distribution) of a Markov chain, when such a distribution exists. For a continuous time Markov chain with state space \mathcal, transition rate from state i to j given by q_ and equilibrium distribution given by \pi, the global balance equations are given by ::\pi_i = \sum_ \pi_j q_, or equivalently :: \pi_i \sum_ q_ = \sum_ \pi_j q_. for all i \in S. Here \pi_i q_ represents the probability flux from state i to state j. So the left-hand side represents the total flow from out of state ''i'' into states other than ''i'', while the right-hand side represents the total flow out of all states j \neq i into state i. In general it is computationa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Pollaczek
Felix may refer to: * Felix (name), people and fictional characters with the name Places * Arabia Felix is the ancient Latin name of Yemen * Felix, Spain, a municipality of the province Almería, in the autonomous community of Andalusia, Spain * St. Felix, Prince Edward Island, a rural community in Prince County, Prince Edward Island, Canada. * Felix, Ontario, an unincorporated place and railway point in Northeastern Ontario, Canada * St. Felix, South Tyrol, a village in South Tyrol, in northern Italy. * Felix, California, an unincorporated community in Calaveras County Music * Felix (band), a British band * Felix (musician), British DJ * Félix Award, a Quebec music award named after Félix Leclerc Business * Felix (pet food), a brand of cat food sold in most European countries * AB Felix, a Swedish food company * Felix Bus Services of Derbyshire, England * Felix Airways, an airline based in Yemen Science and technology * Apache Felix, an open source OSGi framewo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/G/1
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian (modulated by a Poisson process), service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk. Model definition A queue represented by a M/G/1 queue is a stochastic process whose state space is the set , where the value corresponds to the number of customers in the queue, including any being served. Transitions from state ''i'' to ''i'' + 1 represent the arrival of a new customer: the times between such arrivals have an exponential distribution with parameter λ. Transitions from state ''i'' to ''i'' − 1 represent a customer who has been served, finishing being served an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/D/k Queue
In queueing theory, a discipline within the mathematical theory of probability, an M/D/c queue represents the queue length in a system having ''c'' servers, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. The model is an extension of the M/D/1 queue which has only a single server. Model definition An M/D/''c'' queue is a stochastic process whose state space is the set where the value corresponds to the number of customers in the system, including any currently in service. * Arrivals occur at rate λ according to a Poisson process and move the process from state ''i'' to ''i'' + 1. * Service times are deterministic time ''D'' (serving at rate ''μ'' = 1/''D''). * ''c'' servers serve customers from the front of the queue, according to a first-come, first-served ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/D/1 Queue
In queueing theory, a discipline within the mathematical theory of probability, an M/D/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. An extension of this model with more than one server is the M/D/c queue. Model definition An M/D/1 queue is a stochastic process whose state space is the set where the value corresponds to the number of entities in the system, including any currently in service. * Arrivals occur at rate λ according to a Poisson process and move the process from state ''i'' to ''i'' + 1. * Service times are deterministic time ''D'' (serving at rate ''μ'' = 1/''D''). * A single server serves entities one at a time from the front of the queue, according to a first-come, first-s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions: * The probability distribution of the number ''X'' of Bernoulli trials needed to get one success, supported on the set \; * The probability distribution of the number ''Y'' = ''X'' − 1 of failures before the first success, supported on the set \. Which of these is called the geometric distribution is a matter of convention and convenience. These two different geometric distributions should not be confused with each other. Often, the name ''shifted'' geometric distribution is adopted for the former one (distribution of the number ''X''); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the support explicitly. The geometric distribution gives the probability that the first occurrence of success requires ''k'' independent trials, each with success probability ''p''. If the probability of succe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/G/1 Queue
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian (modulated by a Poisson process), service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk. Model definition A queue represented by a M/G/1 queue is a stochastic process whose state space is the set , where the value corresponds to the number of customers in the queue, including any being served. Transitions from state ''i'' to ''i'' + 1 represent the arrival of a new customer: the times between such arrivals have an exponential distribution with parameter λ. Transitions from state ''i'' to ''i'' − 1 represent a customer who has been served, finishing being served and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Process
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponentially Distributed
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \lam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Probability Distribution")
