|
Fractional Approval Voting
Fractional approval voting is an electoral system using approval ballots (each voter selects one or more candidate alternatives), in which the outcome is ''fractional'': for each alternative ''j'' there is a fraction ''pj'' between 0 and 1, such that the sum of ''pj'' is 1. It can be seen as a generalization of approval voting: in the latter, one candidate wins (''pj'' = 1) and the other candidates lose (''pj'' = 0). The fractions ''pj'' can be interpreted in various ways, depending on the setting. Examples are: * ''Time sharing'': each alternative ''j'' is implemented a fraction ''pj'' of the time (e.g. each candidate ''j'' serves in office a fraction ''pj'' of the term). * ''Budget'' ''distribution'': each alternative ''j'' receives a fraction ''pj'' of the total budget.A video of the EC'21 conference talk/ref> * ''Probabilities'': after the fractional results are computed, there is a lottery for selecting a single candidate, where each candidate ''j'' is elected with probabili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electoral System
An electoral system or voting system is a set of rules that determine how elections and referendums are conducted and how their results are determined. Electoral systems are used in politics to elect governments, while non-political elections may take place in business, non-profit organisations and informal organisations. These rules govern all aspects of the voting process: when elections occur, who is allowed to vote, who can stand as a candidate, how ballots are marked and cast, how the ballots are counted, how votes translate into the election outcome, limits on campaign spending, and other factors that can affect the result. Political electoral systems are defined by constitutions and electoral laws, are typically conducted by election commissions, and can use multiple types of elections for different offices. Some electoral systems elect a single winner to a unique position, such as prime minister, president or governor, while others elect multiple winners, such as me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
No Show Paradox
The participation criterion is a Comparison of electoral systems, voting system criterion. Voting systems that fail the participation criterion are said to exhibit the no show paradox and allow a particularly unusual strategy of tactical voting: abstaining from an election can help a voter's preferred choice win. The criterion has been defined as follows: * In a deterministic framework, the participation criterion says that the addition of a ballot, where candidate A is strictly preferred to candidate B, to an existing tally of votes should not change the winner from candidate A to candidate B. * In a probabilistic framework, the participation criterion says that the addition of a ballot, where each candidate of the set X is strictly preferred to each other candidate, to an existing tally of votes should not reduce the probability that the winner is chosen from the set X. Plurality voting, approval voting, range voting, and the Borda count all satisfy the participation criterion. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Party-approval Voting
Multiwinner approval voting, also called approval-based committee voting, is a multi-winner electoral system that uses approval ballots. Each voter may select ("approve") any number of candidates, and multiple candidates are elected. The number of elected candidates is usually fixed in advance. For example, it can be the number of seats in a country's parliament, or the required number of members in a committee. Multiwinner approval voting is an adaptation of approval voting to multiwinner elections. In a single-winner approval voting system, it is easy to determine the winner: it is the candidate approved by the largest number of voters. In multiwinner approval voting, there are many different ways to decide which candidates will be elected. Majoritarian approval voting Versions Block approval voting (unlimited voting) The straightforward extension of approval balloting to multi-winner elections is called block approval voting and is a type of multiple non-transferable v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Justified Representation
Justified representation (JR) is a criterion for evaluating the fairness of electoral systems in multiwinner voting, particularly in multiwinner approval voting. It can be seen as an adaptation of the proportional representation criterion to approval voting. Definitions One definition for "proportional representation" is that the candidates are partitioned into disjoint parties, and each voter approves all candidates in a single party. For example, suppose we need to elect a committee of size 10. Suppose that exactly 50% of the voters approve all candidates in party A, exactly 30% approve all candidates in party B, and exactly 20% approve all candidates in party C. Then, proportional representation requires that the committee contains exactly 5 candidates from party A, exactly 3 candidates from party B, and exactly 2 candidates from party C. If the fractions are not exact, then some rounding method should be used, and this can be done by various apportionment methods. Howev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SAT Solver
The SAT ( ) is a standardized test widely used for college admissions in the United States. Since its debut in 1926, its name and scoring have changed several times; originally called the Scholastic Aptitude Test, it was later called the Scholastic Assessment Test, then the SAT I: Reasoning Test, then the SAT Reasoning Test, then simply the SAT. The SAT is wholly owned, developed, and published by the College Board, a private, not-for-profit organization in the United States. It is administered on behalf of the College Board by the Educational Testing Service, which until recently developed the SAT as well. The test is intended to assess students' readiness for college. The SAT was originally designed not to be aligned with high school curricula, but several adjustments were made for the version of the SAT introduced in 2016, and College Board president David Coleman has said that he also wanted to make the test reflect more closely what students learn in high school with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
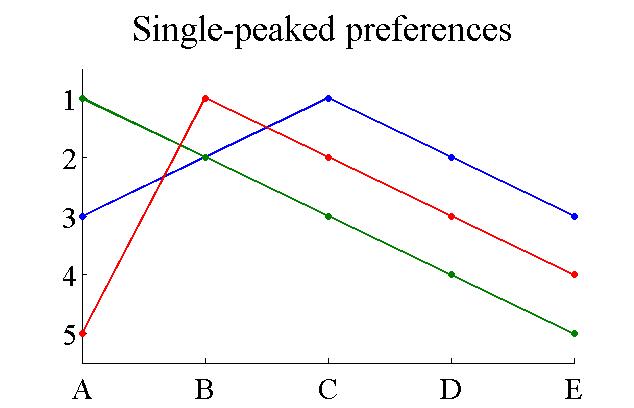
Single-peaked Preferences
Single-peaked preferences are a class of preference relations. A group of agents is said to have single-peaked preferences over a set of possible outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and - # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome: it is to select the median quantity. See the median voter theorem. It is truthful because the median function satisfies the strong monotonicity property ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Permutation
A random permutation is a random ordering of a set of objects, that is, a permutation-valued random variable. The use of random permutations is often fundamental to fields that use randomized algorithms such as coding theory, cryptography, and simulation. A good example of a random permutation is the shuffling of a deck of cards: this is ideally a random permutation of the 52 cards. Generating random permutations Entry-by-entry brute force method One method of generating a random permutation of a set of length ''n'' uniformly at random (i.e., each of the ''n''! permutations is equally likely to appear) is to generate a sequence by taking a random number between 1 and ''n'' sequentially, ensuring that there is no repetition, and interpreting this sequence (''x''1, ..., ''x''''n'') as the permutation : \begin 1 & 2 & 3 & \cdots & n \\ x_1 & x_2 & x_3 & \cdots & x_n \\ \end, shown here in two-line notation. This brute-force method will require occasional retries whenever the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutation
In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set. Permutations differ from combinations, which are selections of some members of a set regardless of order. For example, written as tuples, there are six permutations of the set , namely (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). These are all the possible orderings of this three-element set. Anagrams of words whose letters are different are also permutations: the letters are already ordered in the original word, and the anagram is a reordering of the letters. The study of permutations of finite sets is an important topic in the fields of combinatorics and group theory. Permutations are used in almost every branch of mathematics, and in many other fields of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dictatorship Mechanism
In social choice theory, a dictatorship mechanism is a rule by which, among all possible alternatives, the results of voting mirror a single pre-determined person's preferences, without consideration of the other voters. Dictatorship by itself is not considered a good mechanism in practice, but it is theoretically important: by Arrow's impossibility theorem, when there are at least three alternatives, dictatorship is the only ranked voting electoral system that satisfies ''unrestricted domain'', ''Pareto efficiency'', and ''independence of irrelevant alternatives''. Similarly, by Gibbard's theorem, when there are at least three alternatives, dictatorship is the only ''strategyproof'' rule. Non-dictatorship is a property of more common voting rules, in which the results are influenced by the preferences of all individuals. This property is satisfied if there is no single voter ''i'' with the individual preference order P, such that P is always the societal ("winning") preference or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concave Function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex. Definition A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be ''concave'' if, for any x and y in the interval and for any \alpha \in ,1/math>, :f((1-\alpha )x+\alpha y)\geq (1-\alpha ) f(x)+\alpha f(y) A function is called ''strictly concave'' if :f((1-\alpha )x + \alpha y) > (1-\alpha) f(x) + \alpha f(y)\, for any \alpha \in (0,1) and x \neq y. For a function f: \mathbb \to \mathbb, this second definition merely states that for every z strictly between x and y, the point (z, f(z)) on the graph of f is above the straight line joining the points (x, f(x)) and (y, f(y)). A function f is quasiconcave if the upper contour sets of the function S(a)=\ are convex sets. Properties Functions of a single variable # A differentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Egalitarian Rule
In social choice and operations research, the egalitarian rule (also called the max-min rule or the Rawlsian rule) is a rule saying that, among all possible alternatives, society should pick the alternative which maximizes the ''minimum utility'' of all individuals in society. It is a formal mathematical representation of the egalitarian philosophy. It also corresponds to John Rawls' principle of maximizing the welfare of the worst-off individual. Definition Let X be a set of possible `states of the world' or `alternatives'. Society wishes to choose a single state from X. For example, in a single-winner election, X may represent the set of candidates; in a resource allocation setting, X may represent all possible allocations. Let I be a finite set, representing a collection of individuals. For each i \in I, let u_i:X\longrightarrow\mathbb be a ''utility function'', describing the amount of happiness an individual ''i'' derives from each possible state. A '' social choice rule' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems admit polynomial-time algorithms, whereas mathematical optimization is in general NP-hard. Convex optimization has applications in a wide range of disciplines, such as automatic control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, finance, statistics (optimal experimental design), and structural optimization, where the approximation concept has proven to be efficient. With recent advancements in computing and optimization algorithms, convex programming is nearly as straightforward as linear programming. Definition A convex optimization problem is an optimization problem in which the objective function is a convex function and the feasible set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |