|
Formal Proof
In logic and mathematics, a formal proof or derivation is a finite sequence of sentences (known as well-formed formulas when relating to formal language), each of which is an axiom, an assumption, or follows from the preceding sentences in the sequence, according to the rule of inference. It differs from a natural language argument in that it is rigorous, unambiguous and mechanically verifiable. If the set of assumptions is empty, then the last sentence in a formal proof is called a theorem of the formal system. The notion of theorem is generally effective, but there may be no method by which we can reliably find proof of a given sentence or determine that none exists. The concepts of Fitch-style proof, sequent calculus and natural deduction are generalizations of the concept of proof. The theorem is a syntactic consequence of all the well-formed formulas preceding it in the proof. For a well-formed formula to qualify as part of a proof, it must be the result of applying a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to wor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interactive Theorem Proving
In computer science and mathematical logic, a proof assistant or interactive theorem prover is a software tool to assist with the development of formal proofs by human–machine collaboration. This involves some sort of interactive proof editor, or other interface, with which a human can guide the search for proofs, the details of which are stored in, and some steps provided by, a computer. A recent effort within this field is making these tools use artificial intelligence to automate the formalization of ordinary mathematics. System comparison * ACL2 – a programming language, a first-order logical theory, and a theorem prover (with both interactive and automatic modes) in the Boyer–Moore tradition. * Rocq (formerly known as ''Coq'') – Allows the expression of mathematical assertions, mechanically checks proofs of these assertions, helps to find formal proofs, and extracts a certified program from the constructive proof of its formal specification. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transformation Rule
Rules of inference are ways of deriving conclusions from premises. They are integral parts of formal logic, serving as norms of the logical structure of valid arguments. If an argument with true premises follows a rule of inference then the conclusion cannot be false. ''Modus ponens'', an influential rule of inference, connects two premises of the form "if P then Q" and "P" to the conclusion "Q", as in the argument "If it rains, then the ground is wet. It rains. Therefore, the ground is wet." There are many other rules of inference for different patterns of valid arguments, such as ''modus tollens'', disjunctive syllogism, constructive dilemma, and existential generalization. Rules of inference include rules of implication, which operate only in one direction from premises to conclusions, and rules of replacement, which state that two expressions are equivalent and can be freely swapped. Rules of inference contrast with formal fallaciesinvalid argument forms involving logical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semantics
Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction between sense and reference. Sense is given by the ideas and concepts associated with an expression while reference is the object to which an expression points. Semantics contrasts with syntax, which studies the rules that dictate how to create grammatically correct sentences, and pragmatics, which investigates how people use language in communication. Lexical semantics is the branch of semantics that studies word meaning. It examines whether words have one or several meanings and in what lexical relations they stand to one another. Phrasal semantics studies the meaning of sentences by exploring the phenomenon of compositionality or how new meanings can be created by arranging words. Formal semantics (natural language), Formal semantics relies o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alphabet
An alphabet is a standard set of letter (alphabet), letters written to represent particular sounds in a spoken language. Specifically, letters largely correspond to phonemes as the smallest sound segments that can distinguish one word from another in a given language. Not all writing systems represent language in this way: a syllabary assigns symbols to spoken syllables, while logographies assign symbols to words, morphemes, or other semantic units. The first letters were invented in Ancient Egypt to serve as an aid in writing Egyptian hieroglyphs; these are referred to as Egyptian uniliteral signs by lexicographers. This system was used until the 5th century AD, and fundamentally differed by adding pronunciation hints to existing hieroglyphs that had previously carried no pronunciation information. Later on, these phonemic symbols also became used to transcribe foreign words. The first fully phonemic script was the Proto-Sinaitic script, also descending from Egyptian hi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String (computer Science)
In computer programming, a string is traditionally a sequence of character (computing), characters, either as a literal (computer programming), literal constant or as some kind of Variable (computer science), variable. The latter may allow its elements to be Immutable object, mutated and the length changed, or it may be fixed (after creation). A string is often implemented as an array data structure of bytes (or word (computer architecture), words) that stores a sequence of elements, typically characters, using some character encoding. More general, ''string'' may also denote a sequence (or List (abstract data type), list) of data other than just characters. Depending on the programming language and precise data type used, a variable (programming), variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears lit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation. The general study of interpretations of formal languages is called formal semantics. The most commonly studied formal logics are propositional logic, predicate logic and their modal analogs, and for these there are standard ways of presenting an interpretation. In these contexts an interpretation is a function that provides the extension of symbols and strings of an object language. For example, an interpretation function could take the predicate symbol T and assign it the extension \. All our interpretation does is assign the extension \ to the non-logical symbol T, and does not make a claim about whether T is to stand for tall and \mathrm for Abraham Lincoln. On the other hand, an interpretation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meaning (linguistics)
Semantics is the study of linguistic Meaning (philosophy), meaning. It examines what meaning is, how words get their meaning, and how the meaning of a complex expression depends on its parts. Part of this process involves the distinction between sense and reference. Sense is given by the ideas and concepts associated with an expression while reference is the object to which an expression points. Semantics contrasts with syntax, which studies the rules that dictate how to create grammatically correct sentences, and pragmatics, which investigates how people use language in communication. Lexical semantics is the branch of semantics that studies word meaning. It examines whether words have one or several meanings and in what lexical relations they stand to one another. Phrasal semantics studies the meaning of sentences by exploring the phenomenon of compositionality or how new meanings can be created by arranging words. Formal semantics (natural language), Formal semantics relies o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
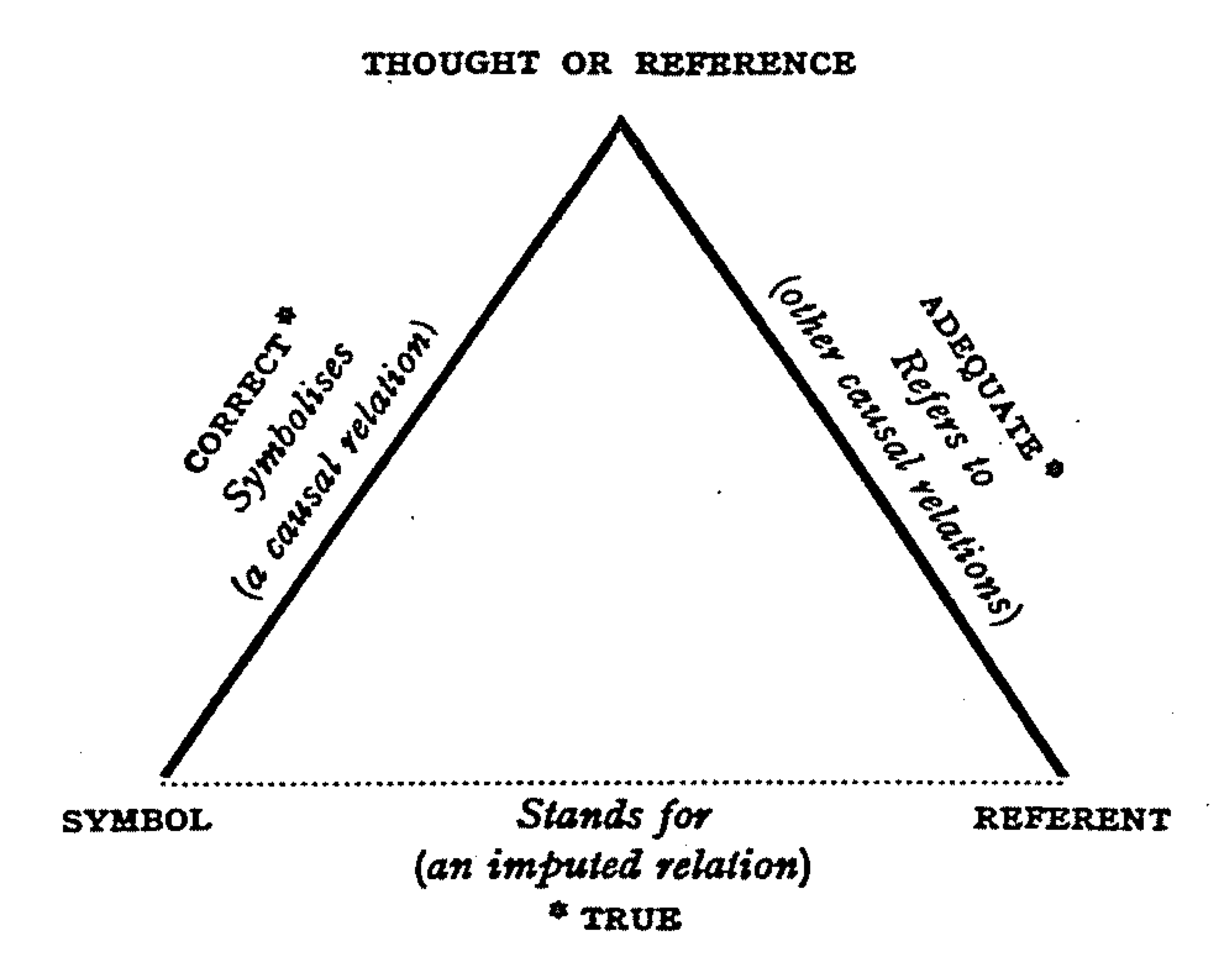
Reference
A reference is a relationship between objects in which one object designates, or acts as a means by which to connect to or link to, another object. The first object in this relation is said to ''refer to'' the second object. It is called a ''name'' for the second object. The next object, the one to which the first object refers, is called the '' referent'' of the first object. A name is usually a phrase or expression, or some other symbolic representation. Its referent may be anything – a material object, a person, an event, an activity, or an abstract concept. References can take on many forms, including: a thought, a sensory perception that is audible ( onomatopoeia), visual (text), olfactory, or tactile, emotional state, relationship with other, spacetime coordinates, symbolic or alpha-numeric, a physical object, or an energy projection. In some cases, methods are used that intentionally hide the reference from some observers, as in cryptography. References feature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symbol
A symbol is a mark, Sign (semiotics), sign, or word that indicates, signifies, or is understood as representing an idea, physical object, object, or wikt:relationship, relationship. Symbols allow people to go beyond what is known or seen by creating linkages between otherwise different concepts and experiences. All communication is achieved through the use of symbols: for example, a red octagon is a common symbol for "Stop sign, STOP"; on maps, blue lines often represent rivers; and a red rose often symbolizes love and compassion. Numerical digit, Numerals are symbols for numbers; Letter (alphabet), letters of an alphabet may be symbols for certain phonemes; and personal names are symbols representing individuals. The academic study of symbols is called semiotics. In the arts, Artistic symbol, symbolism is the use of a abstract and concrete, concrete element to represent a more abstract idea. In cartography, an organized collection of symbols forms a map layout, legend for a ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence (mathematics)
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter "M" first and "Y" last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be '' finite'', as in these examples, or '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |