|
Fluctuation Theorem
The fluctuation theorem (FT), which originated from statistical mechanics, deals with the relative probability that the Entropy (statistical thermodynamics), entropy of a system which is currently away from thermodynamic equilibrium (i.e., maximum entropy) will increase or decrease over a given amount of time. While the second law of thermodynamics predicts that the entropy of an isolated system should tend to increase until it reaches equilibrium, it became apparent after the discovery of statistical mechanics that the second law is only a statistical one, suggesting that there should always be some nonzero probability that the entropy of an isolated system might spontaneously ''decrease''; the fluctuation theorem precisely quantifies this probability. Statement Roughly, the fluctuation theorem relates to the probability distribution of the time-averaged irreversible entropy production, denoted \overline_t. The theorem states that, in systems away from equilibrium over a fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ..., information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Force Microscope
Atomic force microscopy (AFM) or scanning force microscopy (SFM) is a very-high-resolution type of scanning probe microscopy (SPM), with demonstrated resolution on the order of fractions of a nanometer, more than 1000 times better than the diffraction-limited system, optical diffraction limit. Overview Atomic force microscopy (AFM) gathers information by "feeling" or "touching" the surface with a mechanical probe. Piezoelectric elements that facilitate tiny but accurate and precise movements on (electronic) command enable precise scanning. Despite the name, the Atomic Force Microscope does not use the nuclear force. Abilities and spatial resolution The AFM has three major abilities: force measurement, topographic imaging, and manipulation. In force measurement, AFMs can be used to measure the forces between the probe and the sample as a function of their mutual separation. This can be applied to perform force spectroscopy, to measure the mechanical properties of the sample, s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics involved Scientific Revolution, substantial change in the methods and philosophy of physics. The qualifier ''classical'' distinguishes this type of mechanics from physics developed after the History of physics#20th century: birth of modern physics, revolutions in physics of the early 20th century, all of which revealed limitations in classical mechanics. The earliest formulation of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts based on the 17th century foundational works of Sir Isaac Newton, and the mathematical methods invented by Newton, Gottfried Wilhelm Leibniz, Leonhard Euler and others to describe the motion of Physical body, bodies under the influence of forces. Later, methods bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Laws Of Motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows: # A body remains at rest, or in motion at a constant speed in a straight line, unless it is acted upon by a force. # At any instant of time, the net force on a body is equal to the body's acceleration multiplied by its mass or, equivalently, the rate at which the body's momentum is changing with time. # If two bodies exert forces on each other, these forces have the same magnitude but opposite directions. The three laws of motion were first stated by Isaac Newton in his ''Philosophiæ Naturalis Principia Mathematica'' (''Mathematical Principles of Natural Philosophy''), originally published in 1687. Newton used them to investigate and explain the motion of many physical objects and systems. In the time since Newton, new insights, especially around t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jarzynski Equality
The Jarzynski equality (JE) is an equation in statistical mechanics that relates free energy differences between two states and the irreversible work along an ensemble of trajectories joining the same states. It is named after the physicist Christopher Jarzynski (then at the University of Washington and Los Alamos National Laboratory, currently at the University of Maryland) who derived it in 1996. Fundamentally, the Jarzynski equality points to the fact that the fluctuations in the work satisfy certain constraints separately from the average value of the work that occurs in some process. Overview In thermodynamics, the free energy difference \Delta F = F_B - F_A between two states ''A'' and ''B'' is connected to the work ''W'' done on the system through the ''inequality'': : \Delta F \leq W , with equality holding only in the case of a quasistatic process, i.e. when one takes the system from ''A'' to ''B'' infinitely slowly (such that all intermediate states are in thermodyna ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Limit Theorem
In probability theory, the central limit theorem (CLT) states that, under appropriate conditions, the Probability distribution, distribution of a normalized version of the sample mean converges to a Normal distribution#Standard normal distribution, standard normal distribution. This holds even if the original variables themselves are not Normal distribution, normally distributed. There are several versions of the CLT, each applying in the context of different conditions. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern form it was only precisely stated as late as 1920. In statistics, the CLT can be stated as: let X_1, X_2, \dots, X_n denote a Sampling ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Causation
Universal causation is the proposition that everything in the universe has a cause and is thus an effect of that cause. This means that if a given event occurs, then this is the result of a previous, related event. If an object is in a certain state, then it is in that state as a result of another object interacting with it previously. The idea of universal causation is formulated in western philosophy similarly for ages, however the formulations contain some profound differences in methodology and philosophical assumptions. Examples: In contrast, Bertrand Russell argued (in 1912) that the law of causation as usually stated by philosophers is false and is not used in sciences (maybe with exception of their infancy). However his position on universal causation evolved and "was not as naive as it may have appeared". In 1927 Russell writes that the notion of universal causation marks the beginnings of science and philosophy. Philosophers who do believe in exception-less, universal, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-equilibrium Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science, information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. While classical thermodynamics is primarily concerned with thermodynamic equilibrium, statistical mechanics has been applied in non-equilibrium statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loschmidt's Paradox
In physics, Loschmidt's paradox (named for Josef Loschmidt), also known as the reversibility paradox, irreversibility paradox, or ' (), is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics. This puts the time reversal symmetry of (almost) all known low-level fundamental physical processes at odds with any attempt to infer from them the second law of thermodynamics, which describes the behaviour of macroscopic systems. Both of these are well-accepted principles in physics, with sound observational and theoretical support, yet they seem to be in conflict, hence the paradox. Origin Josef Loschmidt's criticism was provoked by the H-theorem of Boltzmann, which employed kinetic theory to explain the increase of entropy in an ideal gas from a non-equilibrium state, when the molecules of the gas are allowed to collide. In 1876, Loschmidt pointed out that if there is a motion of a system from time ''t''0 to time ''t''1 to tim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
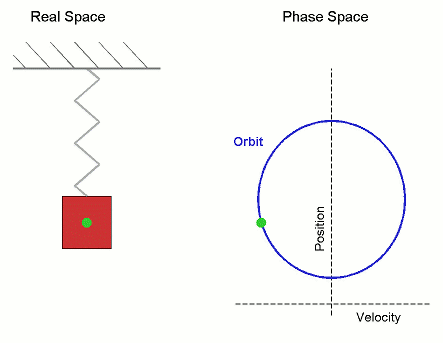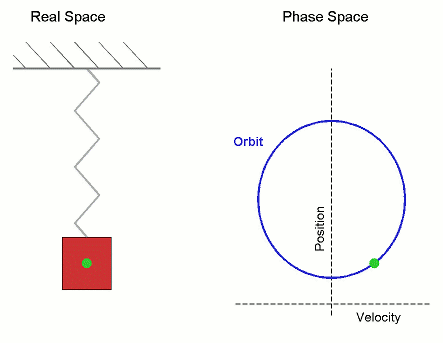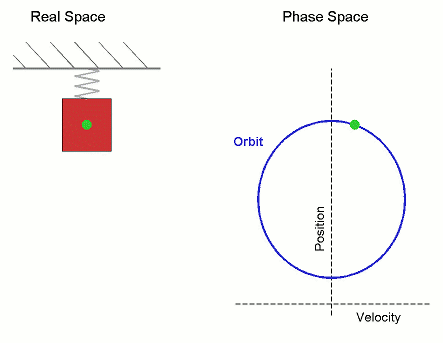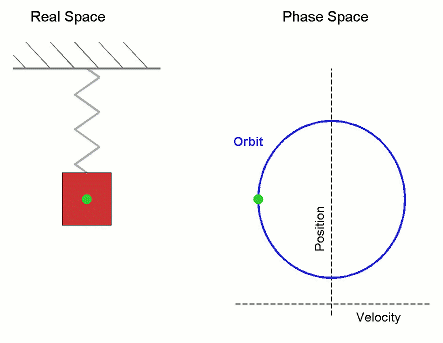
Phase Space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |