|
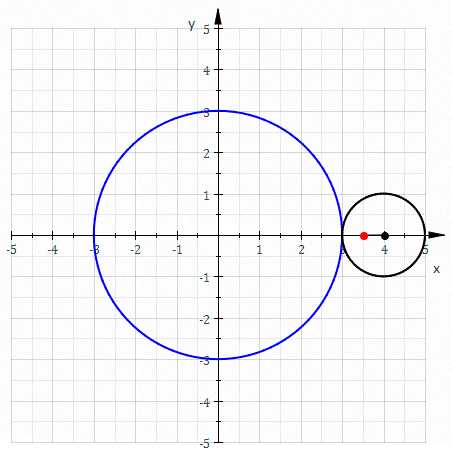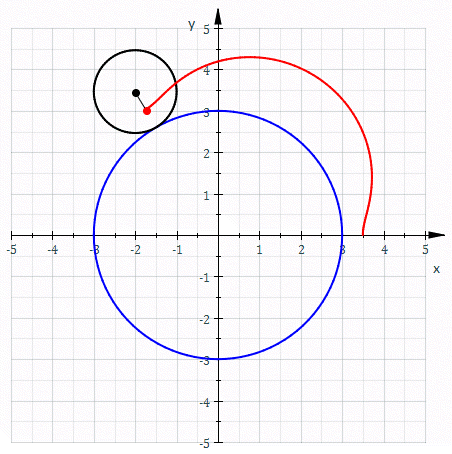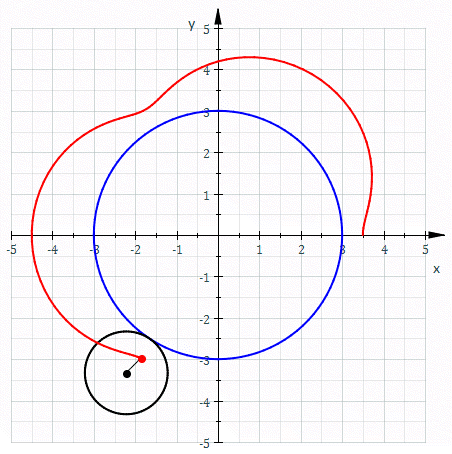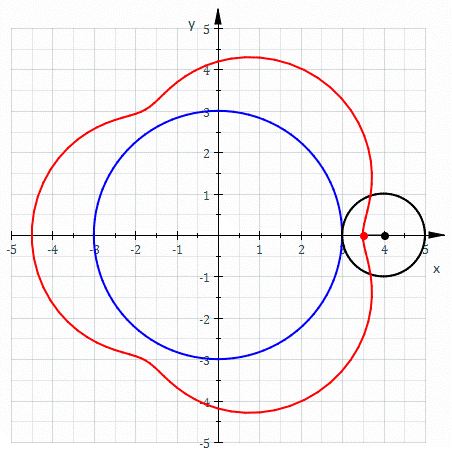
Epicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an ''epicycle''—which rolls without slipping around a fixed circle. It is a particular kind of roulette. Equations If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R + r) \cos \theta \ - r \cos \left( \frac \theta \right) \\ & y (\theta) = (R + r) \sin \theta \ - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k + 1) \cos \theta - r \cos \left( (k + 1) \theta \right) \\ & y (\theta) = r (k + 1) \sin \theta - r \sin \left( (k + 1) \theta \right) \end in a more concise and complex form :z(\theta) = r \left(e^ - (k + 1)e^ \right) where * angle is in turns: \theta \in , 2\pi * smaller circle has radius * the larger circle has radius Area (Assuming the initial point lies on the larger circle.) When is a pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid created by rolling a circle on a line. Properties If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R - r) \cos \theta + r \cos \left(\frac \theta \right) \\ & y (\theta) = (R - r) \sin \theta - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k - 1) \cos \theta + r \cos \left( (k - 1) \theta \right) \\ & y (\theta) = r (k - 1) \sin \theta - r \sin \left( (k - 1) \theta \right) \end If is an integer, then the curve is closed, and has Cusp (singularity), cusps (i.e., sharp corners, where the curve is not Differentiable function, differentiable). Specially for the curve is a straight line and the circles are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deferent And Epicycle
In the Hipparchian, Ptolemaic, and Copernican systems of astronomy, the epicycle (, meaning "circle moving on another circle") was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets. In particular it explained the apparent retrograde motion of the five planets known at the time. Secondarily, it also explained changes in the apparent distances of the planets from the Earth. It was first proposed by Apollonius of Perga at the end of the 3rd century BC. It was developed by Apollonius of Perga and Hipparchus of Rhodes, who used it extensively, during the 2nd century BC, then formalized and extensively used by Ptolemy in his 2nd century AD astronomical treatise the ''Almagest''. Epicyclical motion is used in the Antikythera mechanism, an ancient Greek astronomical device for compensating for the elliptical orbit of the Moon, moving faster at perigee and slower at apogee than circular orbits would, using four ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle. The name was coined by de Castillon in 1741 but the cardioid had been the subject of study decades beforehand.Yates Named for its heart-like form, it is shaped more like the outline of the cross section of a round apple without the stalk. A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the microphone which is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Periodic Functions
This is a list of some well-known periodic functions. The constant function , where is independent of , is periodic with any period, but lacks a ''fundamental period''. A definition is given for some of the following functions, though each function may have many equivalent definitions. Smooth functions All trigonometric functions listed have period 2\pi, unless otherwise stated. For the following trigonometric functions: : is the th up/down number, : is the th Bernoulli number Non-smooth functions The following functions have period p and take x as their argument. The symbol \lfloor n \rfloor is the floor function of n and \sgn is the sign function. Vector-valued functions * Epitrochoid * Epicycloid (special case of the epitrochoid) * Limaçon (special case of the epitrochoid) * Hypotrochoid * Hypocycloid (special case of the hypotrochoid) * Spirograph (special case of the hypotrochoid) Doubly periodic functions * Jacobi's elliptic functions * Weierstrass's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician John Wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle. The parametric equations for an epitrochoid are :\begin & x (\theta) = (R + r)\cos\theta - d\cos\left(\theta\right) \\ & y (\theta) = (R + r)\sin\theta - d\sin\left(\theta\right) \end The parameter is geometrically the polar angle of the center of the exterior circle. (However, is not the polar angle of the point (x(\theta),y(\theta)) on the epitrochoid.) Special cases include the limaçon with and the epicycloid with . The classic Spirograph toy traces out epitrochoid and hypotrochoid curves. The orbits of planets in the once popular geocentric Ptolemaic system are epitrochoids (see deferent and epicycle). The orbit of the moon, when centered around the sun, approximates an epitrochoid. The combustion chamber of the Wankel engine is an epitroch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclogon
In geometry, a cyclogon is the curve traced by a vertex of a polygon that rolls without slipping along a straight line. There are no restrictions on the nature of the polygon. It can be a regular polygon like an equilateral triangle or a square. The polygon need not even be convex: it could even be a star-shaped polygon. More generally, the curves traced by points other than vertices have also been considered. In such cases it would be assumed that the tracing point is rigidly attached to the polygon. If the tracing point is located outside the polygon, then the curve is called a ''prolate cyclogon'', and if it lies inside the polygon it is called a ''curtate cyclogon''. In the limit, as the number of sides increases to infinity, the cyclogon becomes a cycloid. The cyclogon has an interesting property regarding its area. Let denote the area of the region above the line and below one of the arches, let denote the area of the rolling polygon, and let denote the area of the disk ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epicyclic Gearing
An epicyclic gear train (also known as a planetary gearset) consists of two gears mounted so that the center of one gear revolves around the center of the other. A carrier connects the centers of the two gears and rotates the planet and sun gears mesh so that their pitch circles roll without slip. A point on the pitch circle of the planet gear traces an epicycloid curve. In this simplified case, the sun gear is fixed and the planetary gear(s) roll around the sun gear. An epicyclic gear train can be assembled so the planet gear rolls on the inside of the pitch circle of a fixed, outer gear ring, or ring gear, sometimes called an ''annular gear''. In this case, the curve traced by a point on the pitch circle of the planet is a hypocycloid. The combination of epicycle gear trains with a planet engaging both a sun gear and a ring gear is called a ''planetary gear train''.J. J. Uicker, G. R. Pennock and J. E. Shigley, 2003, ''Theory of Machines and Mechanisms,'' Oxford University Pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle. The parametric equations for an epitrochoid are :\begin & x (\theta) = (R + r)\cos\theta - d\cos\left(\theta\right) \\ & y (\theta) = (R + r)\sin\theta - d\sin\left(\theta\right) \end The parameter is geometrically the polar angle of the center of the exterior circle. (However, is not the polar angle of the point (x(\theta),y(\theta)) on the epitrochoid.) Special cases include the limaçon with and the epicycloid with . The classic Spirograph toy traces out epitrochoid and hypotrochoid curves. The orbits of planets in the once popular geocentric Ptolemaic system are epitrochoids (see deferent and epicycle). The orbit of the moon, when centered around the sun, approximates an epitrochoid. The combustion chamber of the Wankel engine is an epitroch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypotrochoid
In geometry, a hypotrochoid is a roulette traced by a point attached to a circle of radius rolling around the inside of a fixed circle of radius , where the point is a distance from the center of the interior circle. The parametric equations for a hypotrochoid are: :\begin & x (\theta) = (R - r)\cos\theta + d\cos\left(\theta\right) \\ & y (\theta) = (R - r)\sin\theta - d\sin\left(\theta\right) \end where is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because is not the polar angle). When measured in radian, takes values from 0 to 2 \pi \times \tfrac (where is least common multiple). Special cases include the hypocycloid with and the ellipse with and . The eccentricity of the ellipse is :e=\frac becoming 1 when d=r (see Tusi couple). The classic Spirograph toy traces out hypotrochoid and epitrochoid curves. Hypotrochoids describe the support of the eigenvalues of some random matrices with cyclic correlation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rolling curve is a circle and the fixed curve is a line then the roulette is a trochoid. If, in this case, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rolling curve is a circle and the fixed curve is a line then the roulette is a trochoid. If, in this case, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |