|
Energy Cascade
In continuum mechanics, an energy cascade involves the transfer of energy from large scales of motion to the small scales (called a direct energy cascade) or a transfer of energy from the small scales to the large scales (called an inverse energy cascade). This transfer of energy between different scales requires that the dynamics of the system is nonlinear. Strictly speaking, a cascade requires the energy transfer to be local in scale (only between fluctuations of nearly the same size), evoking a cascading waterfall from pool to pool without long-range transfers across the scale domain. This concept plays an important role in the study of well-developed turbulence. It was memorably expressed in this poem by Lewis F. Richardson in the 1920s. Energy cascades are also important for wind waves in the theory of wave turbulence. Consider for instance turbulence generated by the air flow around a tall building: the energy-containing eddies generated by flow separation have sizes of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
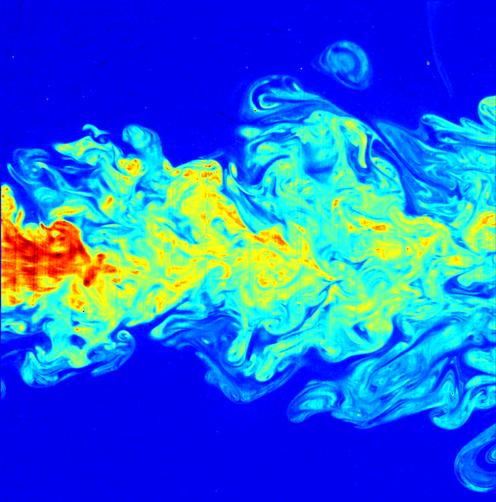
False Color Image Of The Far Field Of A Submerged Turbulent Jet , falsehood in Hindu mythology
{{Disambiguation ...
False or falsehood may refer to: *False (logic), the negation of truth in classical logic *Lie or falsehood, a type of deception in the form of an untruthful statement *false (Unix), a Unix command * ''False'' (album), a 1992 album by Gorefest *Matthew Dear or False (born 1979), American DJ and producer * ''Falsehood'' (1952 film), an Italian melodrama film * ''Falsehood'' (2001 film), an American short film See also * *Anrita Adharma is the Sanskrit antonym of dharma. It means "that which is not in accord with the dharma". Connotations include betrayal, discord, disharmony, unnaturalness, wrongness, evil, immorality, unrighteousness, wickedness, and vice..In Indian s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov ( rus, Андре́й Никола́евич Колмого́ров, p=ɐnˈdrʲej nʲɪkɐˈlajɪvʲɪtɕ kəlmɐˈɡorəf, a=Ru-Andrey Nikolaevich Kolmogorov.ogg, 25 April 1903 – 20 October 1987) was a Soviet mathematician who contributed to the mathematics of probability theory, topology, intuitionistic logic, turbulence, classical mechanics, algorithmic information theory and computational complexity. Biography Early life Andrey Kolmogorov was born in Tambov, about 500 kilometers south-southeast of Moscow, in 1903. His unmarried mother, Maria Y. Kolmogorova, died giving birth to him. Andrey was raised by two of his aunts in Tunoshna (near Yaroslavl) at the estate of his grandfather, a well-to-do nobleman. Little is known about Andrey's father. He was supposedly named Nikolai Matveevich Kataev and had been an agronomist. Kataev had been exiled from St. Petersburg to the Yaroslavl province after his participation in the revolutionary movem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young–Laplace Equation
In physics, the Young–Laplace equation () is an algebraic equation that describes the capillary pressure difference sustained across the interface between two static fluids, such as water and air, due to the phenomenon of surface tension or wall tension, although use of the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surfaces. It's a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface (zero thickness): \begin \Delta p &= -\gamma \nabla \cdot \hat n \\ &= -2\gamma H_f \\ &= -\gamma \left(\frac + \frac\right) \end where \Delta p is the Laplace pressure, the pressure difference across the fluid interface (the exterior pressure minus the interior pressure), \gamma is the surface tension (or wall tension), \hat n is the unit norm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Flow
The term shear flow is used in solid mechanics as well as in fluid dynamics. The expression ''shear flow'' is used to indicate: * a shear stress over a distance in a thin-walled structure (in solid mechanics);Higdon, Ohlsen, Stiles and Weese (1960), ''Mechanics of Materials'', article 4-9 (2nd edition), John Wiley & Sons, Inc., New York. Library of Congress CCN 66-25222 * the flow ''induced'' by a force (in a fluid). In solid mechanics For thin-walled profiles, such as that through a beam or semi-monocoque structure, the shear stress distribution through the thickness can be neglected. Furthermore, there is no shear stress in the direction normal to the wall, only parallel. In these instances, it can be useful to express internal shear stress as shear flow, which is found as the shear stress multiplied by the thickness of the section. An equivalent definition for shear flow is the shear force ''V'' per unit length of the perimeter around a thin-walled section. Shear flow has the di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematic Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties is n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Operator
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is the nabla operator), or \Delta. In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian of a function at a point measures by how much the average value of over small spheres or balls centered at deviates from . The Laplace operator is named after the French mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics: the Laplacian of the gravitational potential due to a given mass density distribution is a constant multiple of that densi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Spectrum
A spectrum (plural ''spectra'' or ''spectrums'') is a condition that is not limited to a specific set of values but can vary, without gaps, across a continuum. The word was first used scientifically in optics to describe the rainbow of colors in visible light after passing through a prism. As scientific understanding of light advanced, it came to apply to the entire electromagnetic spectrum. It thereby became a mapping of a range of magnitudes (wavelengths) to a range of qualities, which are the perceived "colors of the rainbow" and other properties which correspond to wavelengths that lie outside of the visible light spectrum. Spectrum has since been applied by analogy to topics outside optics. Thus, one might talk about the " spectrum of political opinion", or the "spectrum of activity" of a drug, or the "autism spectrum". In these uses, values within a spectrum may not be associated with precisely quantifiable numbers or definitions. Such uses imply a broad range of condition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rate Of Strain
In materials science, strain rate is the change in strain (deformation) of a material with respect to time. The strain rate at some point within the material measures the rate at which the distances of adjacent parcels of the material change with time in the neighborhood of that point. It comprises both the rate at which the material is expanding or shrinking (expansion rate), and also the rate at which it is being deformed by progressive shearing without changing its volume (shear rate). It is zero if these distances do not change, as happens when all particles in some region are moving with the same velocity (same speed and direction) and/or rotating with the same angular velocity, as if that part of the medium were a rigid body. The strain rate is a concept of materials science and continuum mechanics that plays an essential role in the physics of fluids and deformable solids. In an isotropic Newtonian fluid, in particular, the viscous stress is a linear function of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Energy
The term "thermal energy" is used loosely in various contexts in physics and engineering. It can refer to several different well-defined physical concepts. These include the internal energy or enthalpy of a body of matter and radiation; heat, defined as a type of energy transfer (as is thermodynamic work); and the characteristic energy of a degree of freedom, k_T, in a system that is described in terms of its microscopic particulate constituents (where T denotes temperature and k_ denotes the Boltzmann constant). Relation to heat and internal energy In thermodynamics, heat is energy transferred to or from a thermodynamic system by mechanisms other than thermodynamic work or transfer of matter, such as conduction, radiation, and friction. Heat refers to a quantity transferred between systems, not to a property of any one system, or "contained" within it. On the other hand, internal energy and enthalpy are properties of a single system. Heat and work depend on the way in which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Energy
In Outline of physical science, physical sciences, mechanical energy is the sum of potential energy and kinetic energy. The principle of conservation of mechanical energy states that if an isolated system is subject only to conservative forces, then the mechanical energy is constant. If an object moves in the opposite direction of a conservative net force, the potential energy will increase; and if the speed (not the velocity) of the object changes, the kinetic energy of the object also changes. In all real systems, however, nonconservative forces, such as frictional forces, will be present, but if they are of negligible Magnitude (mathematics), magnitude, the mechanical energy changes little and its conservation is a useful approximation. In elastic collisions, the kinetic energy is conserved, but in inelastic collisions some mechanical energy may be converted into thermal energy. The equivalence between lost mechanical energy and an increase in temperature was discovered by Jame ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction: *Dry friction is a force that opposes the relative lateral motion of two solid surfaces in contact. Dry friction is subdivided into ''static friction'' ("stiction") between non-moving surfaces, and ''kinetic friction'' between moving surfaces. With the exception of atomic or molecular friction, dry friction generally arises from the interaction of surface features, known as asperities (see Figure 1). *Fluid friction describes the friction between layers of a viscous fluid that are moving relative to each other. *Lubricated friction is a case of fluid friction where a lubricant fluid separates two solid surfaces. *Skin friction is a component of drag, the force resisting the motion of a fluid across the surface of a body. *Internal friction is the force resisting motion between the elements making up a so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest. Formally, a kinetic energy is any term in a system's Lagrangian which includes a derivative with respect to time. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2. In relativistic mechanics, this is a good approximation only when ''v'' is much less than the speed of light. The standard unit of kinetic energy is the joule, while the English unit of kinetic energy is the foot-pound. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |