|
Elliptic Coordinate System
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal ellipses and hyperbolae. The two foci F_ and F_ are generally taken to be fixed at -a and +a, respectively, on the x-axis of the Cartesian coordinate system. Basic definition The most common definition of elliptic coordinates (\mu, \nu) is : x = a \ \cosh \mu \ \cos \nu : y = a \ \sinh \mu \ \sin \nu where \mu is a nonnegative real number and \nu \in , 2\pi On the complex plane, an equivalent relationship is : x + iy = a \ \cosh(\mu + i\nu) These definitions correspond to ellipses and hyperbolae. The trigonometric identity : \frac + \frac = \cos^ \nu + \sin^ \nu = 1 shows that curves of constant \mu form ellipses, whereas the hyperbolic trigonometric identity : \frac - \frac = \cosh^ \mu - \sinh^ \mu = 1 shows that curves of constant \nu form hyperbolae. Scale factors In an orthogonal coordinate system the lengths of the bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptical Coordinates Grid
Elliptical may mean: * having the shape of an ellipse, or more broadly, any oval shape ** in botany, having an elliptic leaf shape ** of aircraft wings, having an elliptical planform * characterised by ellipsis (the omission of words), or by concision more broadly * an elliptical trainer, an exercise machine See also * Ellipse (other) In mathematics, an ellipse is a geometrical figure. Ellipse may also refer to: *MacAdam ellipse, an area in a chromaticity diagram * Elliptic leaf shape * Superellipse, a geometric figure As a name, it may also be: * The Ellipse, an area in Wa ... * Ellipsis (other) {{Disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivalued Function
In mathematics, a multivalued function, also called multifunction, many-valued function, set-valued function, is similar to a function, but may associate several values to each input. More precisely, a multivalued function from a domain to a codomain associates each in to one or more values in ; it is thus a serial binary relation. Some authors allow a multivalued function to have no value for some inputs (in this case a multivalued function is simply a binary relation). However, in some contexts such as in complex analysis (''X'' = ''Y'' = C), authors prefer to mimic function theory as they extend concepts of the ordinary (single-valued) functions. In this context, an ordinary function is often called a single-valued function to avoid confusion. The term ''multivalued function'' originated in complex analysis, from analytic continuation. It often occurs that one knows the value of a complex analytic function f(z) in some neighbourhood of a point z=a. This is the case fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Coordinates
In analytical mechanics, generalized coordinates are a set of parameters used to represent the state of a system in a configuration space. These parameters must uniquely define the configuration of the system relative to a reference state.,p. 397, §7.2.1 Selection of generalized coordinates/ref> The generalized velocities are the time derivatives of the generalized coordinates of the system. The adjective "generalized" distinguishes these parameters from the traditional use of the term "coordinate" to refer to Cartesian coordinates An example of a generalized coordinate would be to describe the position of a pendulum using the angle of the pendulum relative to vertical, rather than by the x and y position of the pendulum. Although there may be many possible choices for generalized coordinates for a physical system, they are generally selected to simplify calculations, such as the solution of the equations of motion for the system. If the coordinates are independent of o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvilinear Coordinates
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible (a one-to-one map) at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name ''curvilinear coordinates'', coined by the French mathematician Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved. Well-known examples of curvilinear coordinate systems in three-dimensional Euclidean space (R3) are cylindrical and spherical coordinates. A Cartesian coordinate surface in this space is a coordinate plane; for example ''z'' = 0 defines the ''x''-''y'' plane. In the same space, the coordinate surface ''r'' = 1 in spherical coordinates is the surface of a unit sphere, which is curved. The formalism of curvilinear c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum is : \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) and, in a modified form, in electrodynamics, quantum mechanics, quan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separation Of Variables
In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation. Ordinary differential equations (ODE) Suppose a differential equation can be written in the form :\frac f(x) = g(x)h(f(x)) which we can write more simply by letting y = f(x): :\frac=g(x)h(y). As long as ''h''(''y'') ≠ 0, we can rearrange terms to obtain: : = g(x) \, dx, so that the two variables ''x'' and ''y'' have been separated. ''dx'' (and ''dy'') can be viewed, at a simple level, as just a convenient notation, which provides a handy mnemonic aid for assisting with manipulations. A formal definition of ''dx'' as a differential (infinitesimal) is somewhat advanced. Alternative notation Those who dislike Leibniz's notation may prefer to write this as :\frac \frac = g(x), but that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Equation
In mathematics, the eigenvalue problem for the Laplace operator is known as the Helmholtz equation. It corresponds to the linear partial differential equation \nabla^2 f = -k^2 f, where is the Laplace operator (or "Laplacian"), is the eigenvalue, and is the (eigen)function. When the equation is applied to waves, is known as the wave number. The Helmholtz equation has a variety of applications in physics, including the wave equation and the diffusion equation, and it has uses in other sciences. Motivation and uses The Helmholtz equation often arises in the study of physical problems involving partial differential equations (PDEs) in both space and time. The Helmholtz equation, which represents a time-independent form of the wave equation, results from applying the technique of separation of variables to reduce the complexity of the analysis. For example, consider the wave equation \left(\nabla^2-\frac\frac\right) u(\mathbf,t)=0. Separation of variables begins by assumi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace's Equation
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as \nabla^2\! f = 0 or \Delta f = 0, where \Delta = \nabla \cdot \nabla = \nabla^2 is the Laplace operator,The delta symbol, Δ, is also commonly used to represent a finite change in some quantity, for example, \Delta x = x_1 - x_2. Its use to represent the Laplacian should not be confused with this use. \nabla \cdot is the divergence operator (also symbolized "div"), \nabla is the gradient operator (also symbolized "grad"), and f (x, y, z) is a twice-differentiable real-valued function. The Laplace operator therefore maps a scalar function to another scalar function. If the right-hand side is specified as a given function, h(x, y, z), we have \Delta f = h. This is called Poisson's equation, a generalization of Laplace's equation. Laplace's equation and Poisson's equation are the simplest exa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
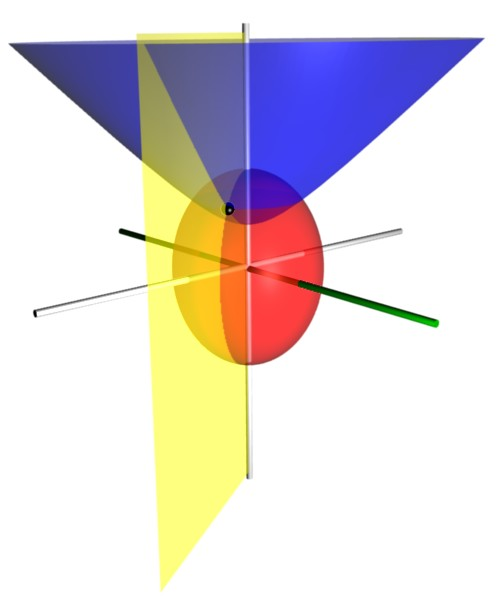
Ellipsoidal Coordinates
Ellipsoidal coordinates are a three-dimensional orthogonal coordinate system (\lambda, \mu, \nu) that generalizes the two-dimensional elliptic coordinate system. Unlike most three-dimensional orthogonal coordinate systems that feature quadratic coordinate surfaces, the ellipsoidal coordinate system is based on confocal quadrics. Basic formulae The Cartesian coordinates (x, y, z) can be produced from the ellipsoidal coordinates ( \lambda, \mu, \nu ) by the equations : x^ = \frac : y^ = \frac : z^ = \frac where the following limits apply to the coordinates : - \lambda < c^ < - \mu < b^ < -\nu < a^. Consequently, surfaces of constant are s : whereas surfaces of constant are |
Oblate Spheroidal Coordinates
Oblate spheroidal coordinates are a three-dimensional orthogonal coordinates, orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinates, elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius a in the ''x''-''y'' plane. (Rotation about the other axis produces prolate spheroidal coordinates.) Oblate spheroidal coordinates can also be considered as a limiting case (mathematics), limiting case of ellipsoidal coordinates in which the two largest semi-axis, semi-axes are equal in length. Oblate spheroidal coordinates are often useful in solving partial differential equations when the boundary conditions are defined on an oblate spheroid or a hyperboloid, hyperboloid of revolution. For example, they played an important role in the calculation of the Perrin friction factors, which contributed to the awarding of the 1926 Nobel Pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prolate Spheroidal Coordinates
Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length. Prolate spheroidal coordinates can be used to solve various partial differential equations in which the boundary conditions match its symmetry and shape, such as solving for a field produced by two centers, which are taken as the foci on the ''z''-axis. One example is solving for the wavefunction of an electron moving in the electromagnetic field of two positively charged nuclei, as in the hydrogen molecular ion, H2+. Another example is solving for the electric field generated by two small electro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |