|
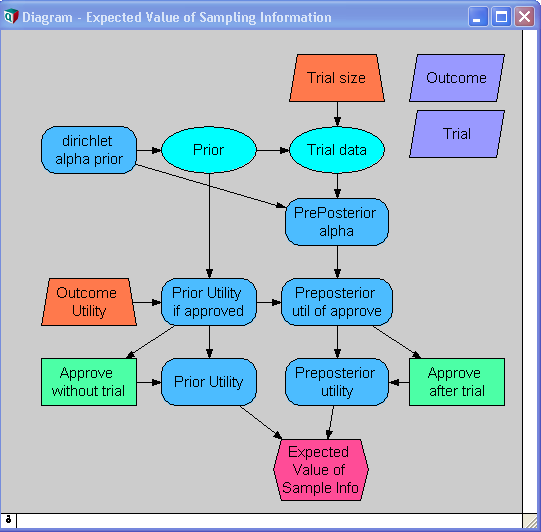
Expected Value Of Sample Information
In decision theory, the expected value of sample information (EVSI) is the expected increase in utility that a decision-maker could obtain from gaining access to a sample of additional observations before making a decision. The additional information obtained from the sample may allow them to make a more informed, and thus better, decision, thus resulting in an increase in expected utility. EVSI attempts to estimate what this improvement would be before seeing actual sample data; hence, EVSI is a form of what is known as ''preposterior analysis''. The use of EVSI in decision theory was popularized by Robert Schlaifer and Howard Raiffa in the 1960s. Formulation Let : \begin d\in D & \mbox D \\ x\in X & \mbox X \\ z \in Z & \mbox n \mbox \langle z_1,z_2,..,z_n \rangle \\ U(d,x) & \mbox d \mbox x \\ p(x) & \mbox x \\ p(z, x) & \mbox z \end It is common (but not essential) in EVSI scenarios for Z_i=X, p(z, x)=\prod p(z_i, x) and \int z p(z, x) dz = x, which is to say that each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decision Theory
Decision theory or the theory of rational choice is a branch of probability theory, probability, economics, and analytic philosophy that uses expected utility and probabilities, probability to model how individuals would behave Rationality, rationally under uncertainty. It differs from the Cognitive science, cognitive and Behavioural sciences, behavioral sciences in that it is mainly Prescriptive economics, prescriptive and concerned with identifying optimal decision, optimal decisions for a rational agent, rather than Descriptive economics, describing how people actually make decisions. Despite this, the field is important to the study of real human behavior by Social science, social scientists, as it lays the foundations to Mathematical model, mathematically model and analyze individuals in fields such as sociology, economics, criminology, cognitive science, moral philosophy and political science. History The roots of decision theory lie in probability theory, developed by Blai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multinomial Distribution
In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided die rolled ''n'' times. For ''n'' statistical independence, independent trials each of which leads to a success for exactly one of ''k'' categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories. When ''k'' is 2 and ''n'' is 1, the multinomial distribution is the Bernoulli distribution. When ''k'' is 2 and ''n'' is bigger than 1, it is the binomial distribution. When ''k'' is bigger than 2 and ''n'' is 1, it is the categorical distribution. The term "multinoulli" is sometimes used for the categorical distribution to emphasize this four-way relationship (so ''n'' determines the suffix, and ''k'' the prefix). The Bernoulli distribution models the outcome of a si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Utility
The expected utility hypothesis is a foundational assumption in mathematical economics concerning decision making under uncertainty. It postulates that rational agents maximize utility, meaning the subjective desirability of their actions. Rational choice theory, a cornerstone of microeconomics, builds this postulate to model aggregate social behaviour. The expected utility hypothesis states an agent chooses between risky prospects by comparing expected utility values (i.e., the weighted sum of adding the respective utility values of payoffs multiplied by their probabilities). The summarised formula for expected utility is U(p)=\sum u(x_k)p_k where p_k is the probability that outcome indexed by k with payoff x_k is realized, and function ''u'' expresses the utility of each respective payoff. Graphically the curvature of the u function captures the agent's risk attitude. For example, imagine you’re offered a choice between receiving $50 for sure, or flipping a coin to win $100 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value Of Including Uncertainty
{{disambig ...
Expected may refer to: *Expectation (epistemic) *Expected value *Expected shortfall *Expected utility hypothesis *Expected return *Expected loss See also *Unexpected (other) *Expected value (other) Expected value is a term used in probability theory and statistics. It may also refer to: Physics * Expectation value (quantum mechanics) In quantum mechanics, the expectation value is the probabilistic expected value of the result (measurement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value Of Perfect Information
In decision theory, the expected value of perfect information (EVPI) is the price that one would be willing to pay in order to gain access to perfect information. A common discipline that uses the EVPI concept is health economics. In that context and when looking at a decision of whether to adopt a new treatment technology, there is always some degree of uncertainty surrounding the decision, because there is always a chance that the decision turns out to be wrong. The expected value of perfect information analysis tries to measure the expected cost of that uncertainty, which “can be interpreted as the expected value of perfect information (EVPI), since perfect information can eliminate the possibility of making the wrong decision” at least from a theoretical perspective. Equation The problem is modeled with a payoff matrix ''Rij'' in which the row index ''i'' describes a choice that must be made by the player, while the column index ''j'' describes a random variable that th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Experimental Design
Bayesian experimental design provides a general probability-theoretical framework from which other theories on experimental design can be derived. It is based on Bayesian inference to interpret the observations/data acquired during the experiment. This allows accounting for both any prior knowledge on the parameters to be determined as well as uncertainties in observations. The theory of Bayesian experimental design is to a certain extent based on the theory for making optimal decisions under uncertainty. The aim when designing an experiment is to maximize the expected utility of the experiment outcome. The utility is most commonly defined in terms of a measure of the accuracy of the information provided by the experiment (e.g., the Shannon information or the negative of the variance) but may also involve factors such as the financial cost of performing the experiment. What will be the optimal experiment design depends on the particular utility criterion chosen. Relations to more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayes' Theorem
Bayes' theorem (alternatively Bayes' law or Bayes' rule, after Thomas Bayes) gives a mathematical rule for inverting Conditional probability, conditional probabilities, allowing one to find the probability of a cause given its effect. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to someone of a known age to be assessed more accurately by conditioning it relative to their age, rather than assuming that the person is typical of the population as a whole. Based on Bayes' law, both the prevalence of a disease in a given population and the error rate of an infectious disease test must be taken into account to evaluate the meaning of a positive test result and avoid the ''base-rate fallacy''. One of Bayes' theorem's many applications is Bayesian inference, an approach to statistical inference, where it is used to invert the probability of Realization (probability), observations given a model configuration (i.e., th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Methods
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on Resampling (statistics), repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic system, deterministic in principle. The name comes from the Monte Carlo Casino in Monaco, where the primary developer of the method, mathematician Stanisław Ulam, was inspired by his uncle's gambling habits. Monte Carlo methods are mainly used in three distinct problem classes: optimization, numerical integration, and generating draws from a probability distribution. They can also be used to model phenomena with significant uncertainty in inputs, such as calculating the risk of a nuclear power plant failure. Monte Carlo methods are often implemented using computer simulations, and they can provide approximate solutions to problems that are otherwise intractable or too complex to analyze mathematically. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value Of Including Uncertainty
{{disambig ...
Expected may refer to: *Expectation (epistemic) *Expected value *Expected shortfall *Expected utility hypothesis *Expected return *Expected loss See also *Unexpected (other) *Expected value (other) Expected value is a term used in probability theory and statistics. It may also refer to: Physics * Expectation value (quantum mechanics) In quantum mechanics, the expectation value is the probabilistic expected value of the result (measurement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value Of Perfect Information
In decision theory, the expected value of perfect information (EVPI) is the price that one would be willing to pay in order to gain access to perfect information. A common discipline that uses the EVPI concept is health economics. In that context and when looking at a decision of whether to adopt a new treatment technology, there is always some degree of uncertainty surrounding the decision, because there is always a chance that the decision turns out to be wrong. The expected value of perfect information analysis tries to measure the expected cost of that uncertainty, which “can be interpreted as the expected value of perfect information (EVPI), since perfect information can eliminate the possibility of making the wrong decision” at least from a theoretical perspective. Equation The problem is modeled with a payoff matrix ''Rij'' in which the row index ''i'' describes a choice that must be made by the player, while the column index ''j'' describes a random variable that th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
EVSI Result
In decision theory, the expected value of sample information (EVSI) is the expected increase in utility that a decision-maker could obtain from gaining access to a sample of additional observations before making a decision. The additional information obtained from the sample may allow them to make a more informed, and thus better, decision, thus resulting in an increase in expected utility. EVSI attempts to estimate what this improvement would be before seeing actual sample data; hence, EVSI is a form of what is known as ''preposterior analysis''. The use of EVSI in decision theory was popularized by Robert Schlaifer and Howard Raiffa in the 1960s. Formulation Let : \begin d\in D & \mbox D \\ x\in X & \mbox X \\ z \in Z & \mbox n \mbox \langle z_1,z_2,..,z_n \rangle \\ U(d,x) & \mbox d \mbox x \\ p(x) & \mbox x \\ p(z, x) & \mbox z \end It is common (but not essential) in EVSI scenarios for Z_i=X, p(z, x)=\prod p(z_i, x) and \int z p(z, x) dz = x, which is to say that each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |