|
Existential Generalization
In predicate logic, existential generalization (also known as existential introduction, ∃I) is a valid rule of inference that allows one to move from a specific statement, or one instance, to a quantified generalized statement, or existential proposition. In first-order logic, it is often used as a rule for the existential quantifier (\exists) in formal proofs. Example: "Rover loves to wag his tail. Therefore, something loves to wag its tail." Example: "Alice made herself a cup of tea. Therefore, Alice made someone a cup of tea." Example: "Alice made herself a cup of tea. Therefore, someone made someone a cup of tea." In the Fitch-style calculus: : Q(a) \to\ \exists\, Q(x) , where Q(a) is obtained from Q(x) by replacing all its free occurrences of x (or some of them) by a. Quine According to Willard Van Orman Quine, universal instantiation and existential generalization are two aspects of a single principle, for instead of saying that \forall x \, x=x implies \text=\text ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rule Of Inference
In the philosophy of logic, a rule of inference, inference rule or transformation rule is a logical form consisting of a function which takes premises, analyzes their syntax, and returns a conclusion (or conclusions). For example, the rule of inference called '' modus ponens'' takes two premises, one in the form "If p then q" and another in the form "p", and returns the conclusion "q". The rule is valid with respect to the semantics of classical logic (as well as the semantics of many other non-classical logics), in the sense that if the premises are true (under an interpretation), then so is the conclusion. Typically, a rule of inference preserves truth, a semantic property. In many-valued logic, it preserves a general designation. But a rule of inference's action is purely syntactic, and does not need to preserve any semantic property: any function from sets of formulae to formulae counts as a rule of inference. Usually only rules that are recursive are important; i.e. ru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jon Barwise
Kenneth Jon Barwise (; June 29, 1942 – March 5, 2000) was an American mathematician, philosopher and logician who proposed some fundamental revisions to the way that logic is understood and used. Education and career Born in Independence, Missouri to Kenneth T. and Evelyn Barwise, Jon was a precocious child. A pupil of Solomon Feferman at Stanford University, Barwise started his research in infinitary logic. After positions as assistant professor at Yale University and the University of Wisconsin, during which time his interests turned to natural language, he returned to Stanford in 1983 to direct the Center for the Study of Language and Information. He began teaching at Indiana University in 1990. He was elected a Fellow of the American Academy of Arts and Sciences in 1999. In his last year, Barwise was invited to give the 2000 Gödel Lecture; he died prior to the lecture. Philosophical and logical work Barwise contended that, by being explicit about the context i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Rules Of Inference
This is a list of rules of inference, logical laws that relate to mathematical formulae. Introduction Rules of inference are syntactical transform rules which one can use to infer a conclusion from a premise to create an argument. A set of rules can be used to infer any valid conclusion if it is complete, while never inferring an invalid conclusion, if it is sound. A sound and complete set of rules need not include every rule in the following list, as many of the rules are redundant, and can be proven with the other rules. ''Discharge rules'' permit inference from a subderivation based on a temporary assumption. Below, the notation : \varphi \vdash \psi indicates such a subderivation from the temporary assumption \varphi to \psi. Rules for classical sentential calculus Sentential calculus is also known as propositional calculus. Rules for negations ;Reductio ad absurdum (or ''Negation Introduction''): : \varphi \vdash \psi : \underline : \lnot \varphi ;Reductio ad absurdum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
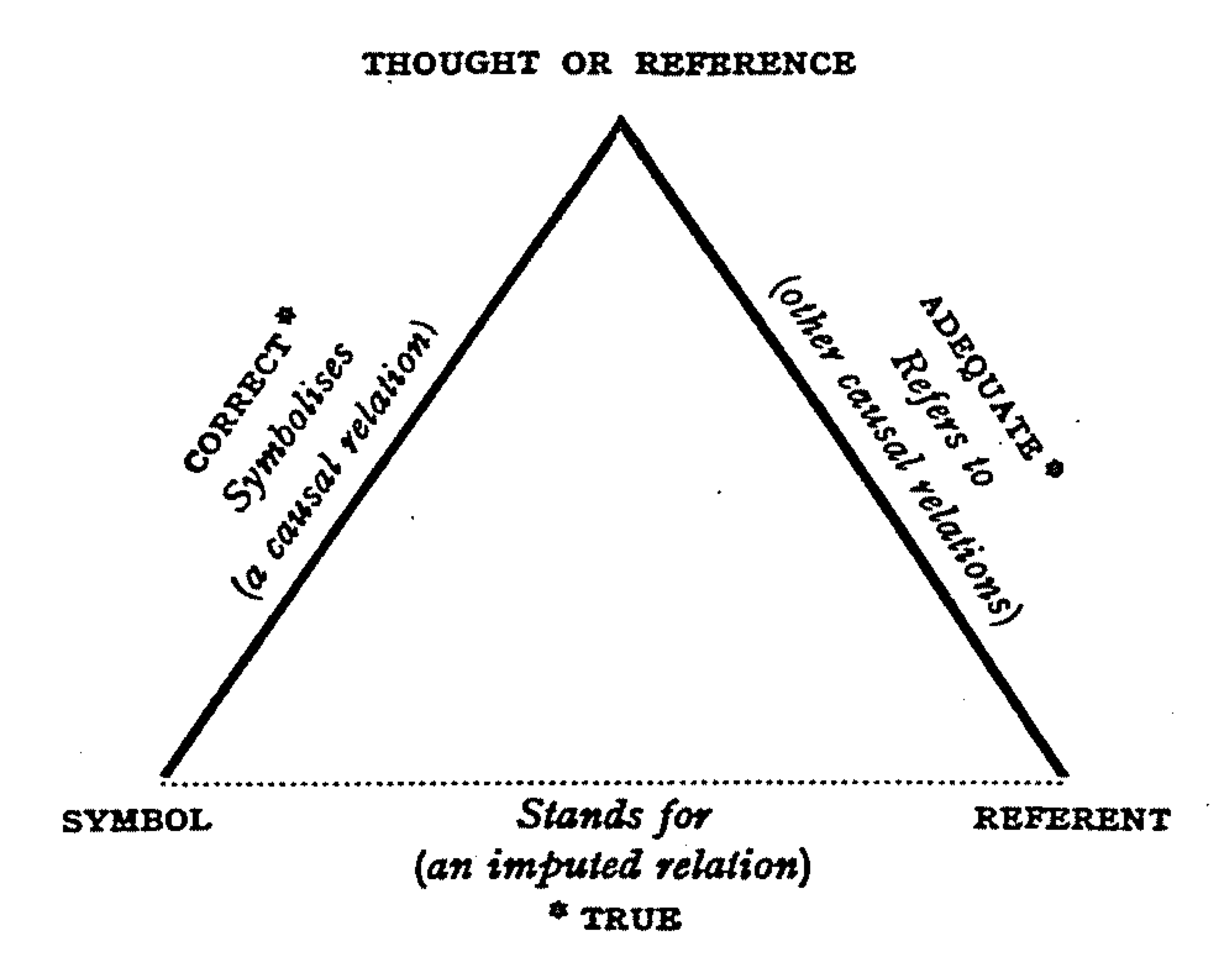
Reference
Reference is a relationship between objects in which one object designates, or acts as a means by which to connect to or link to, another object. The first object in this relation is said to ''refer to'' the second object. It is called a '' name'' for the second object. The second object, the one to which the first object refers, is called the '' referent'' of the first object. A name is usually a phrase or expression, or some other symbolic representation. Its referent may be anything – a material object, a person, an event, an activity, or an abstract concept. References can take on many forms, including: a thought, a sensory perception that is audible ( onomatopoeia), visual (text), olfactory, or tactile, emotional state, relationship with other, spacetime coordinate, symbolic or alpha-numeric, a physical object or an energy projection. In some cases, methods are used that intentionally hide the reference from some observers, as in cryptography. References feature in many ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantification (logic)
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier \forall in the first order formula \forall x P(x) expresses that everything in the domain satisfies the property denoted by P. On the other hand, the existential quantifier \exists in the formula \exists x P(x) expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable. The mostly commonly used quantifiers are \forall and \exists. These quantifiers are standardly defined as duals; in classical logic, they are interdefinable using negation. They can also be used to define more complex quantifiers, as in the formula \neg \exists x P(x) which expresses that nothing has the property P. Other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Instantiation
In predicate logic, universal instantiation (UI; also called universal specification or universal elimination, and sometimes confused with '' dictum de omni'') is a valid rule of inference from a truth about each member of a class of individuals to the truth about a particular individual of that class. It is generally given as a quantification rule for the universal quantifier but it can also be encoded in an axiom schema. It is one of the basic principles used in quantification theory. Example: "All dogs are mammals. Fido is a dog. Therefore Fido is a mammal." Formally, the rule as an axiom schema is given as : \forall x \, A \Rightarrow A\, for every formula ''A'' and every term ''a'', where A\ is the result of substituting ''a'' for each ''free'' occurrence of ''x'' in ''A''. \, A\ is an instance of \forall x \, A. And as a rule of inference it is :from \vdash \forall x A infer \vdash A \ . Irving Copi noted that universal instantiation "...follows from variants of rules ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Willard Van Orman Quine
Willard Van Orman Quine (; known to his friends as "Van"; June 25, 1908 – December 25, 2000) was an American philosopher and logician in the analytic tradition, recognized as "one of the most influential philosophers of the twentieth century". From 1930 until his death 70 years later, Quine was continually affiliated with Harvard University in one way or another, first as a student, then as a professor. He filled the Edgar Pierce Chair of Philosophy at Harvard from 1956 to 1978. Quine was a teacher of logic and set theory. Quine was famous for his position that first order logic is the only kind worthy of the name, and developed his own system of mathematics and set theory, known as New Foundations. In philosophy of mathematics, he and his Harvard colleague Hilary Putnam developed the Quine–Putnam indispensability argument, an argument for the Philosophy of mathematics#Empiricism, reality of mathematical entities.Colyvan, Mark"Indispensability Arguments in the Philosophy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Etchemendy
John W. Etchemendy (born 1952 in Reno, Nevada) is an American logician and philosopher who served as Stanford University's twelfth Provost. He succeeded John L. Hennessy to the post on September 1, 2000 and stepped down on January 31, 2017. Education and career John Etchemendy received his bachelor's and master's degrees at the University of Nevada, Reno before earning his PhD in philosophy at Stanford in 1982. He has been a faculty member in Stanford's Department of Philosophy since 1983, prior to which he was a faculty member in the Philosophy Department at Princeton University. He is also a faculty member of Stanford's Symbolic Systems Program and a senior researcher at the Center for the Study of Language and Information at Stanford. At Stanford, Etchemendy served as director of the Center for the Study of Language and Information from 1990 to 1993, senior associate dean in the School of Humanities and Sciences from 1993 to 1997, and chair of the Department of Philosop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fitch Notation
Fitch notation, also known as Fitch diagrams (named after Frederic Fitch), is a notational system for constructing formal proofs used in sentential logics and predicate logics. Fitch-style proofs arrange the sequence of sentences that make up the proof into rows. A unique feature of Fitch notation is that the degree of indentation of each row conveys which assumptions are active for that step. Example Each row in a Fitch-style proof is either: * an assumption or subproof assumption. * a sentence justified by the citation of (1) a rule of inference and (2) the prior line or lines of the proof that license that rule. Introducing a new assumption increases the level of indentation, and begins a new vertical "scope" bar that continues to indent subsequent lines until the assumption is discharged. This mechanism immediately conveys which assumptions are active for any given line in the proof, without the assumptions needing to be rewritten on every line (as with sequent-style proofs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predicate Logic
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists''"'' is a quantifier, while ''x'' is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic. A theory about a topic is usually a first-order logic together with a specified domain of discourse (over which the quantified variables range), finitely many functions from that domain to itself, finitely many predicates defined on that domain, and a set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Existential Quantifier
In predicate logic, an existential quantification is a type of quantifier, a logical constant which is interpreted as "there exists", "there is at least one", or "for some". It is usually denoted by the logical operator symbol ∃, which, when used together with a predicate variable, is called an existential quantifier ("" or "" or "). Existential quantification is distinct from universal quantification ("for all"), which asserts that the property or relation holds for ''all'' members of the domain. Some sources use the term existentialization to refer to existential quantification. Basics Consider a formula that states that some natural number multiplied by itself is 25. : 0·0 = 25, or 1·1 = 25, or 2·2 = 25, or 3·3 = 25, ... This would seem to be a logical disjunction because of the repeated use of "or". However, the ellipses make this impossible to integrate and to interpret it as a disjunction in formal logic. Instead, the statement could be rephrased more formally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First-order Logic
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists''"'' is a quantifier, while ''x'' is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic. A theory about a topic is usually a first-order logic together with a specified domain of discourse (over which the quantified variables range), finitely many functions from that domain to itself, finitely many predicates defined on that domain, and a set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |