|
Element Uniqueness Problem
In computational complexity theory, the element distinctness problem or element uniqueness problem is the problem of determining whether all the elements of a list are distinct. It is a well studied problem in many different models of computation. The problem may be solved by sorting the list and then checking if there are any consecutive equal elements; it may also be solved in linear expected time by a randomized algorithm that inserts each item into a hash table and compares only those elements that are placed in the same hash table cell. Several lower bounds in computational complexity are proved by reducing the element distinctness problem to the problem in question, i.e., by demonstrating that the solution of the element uniqueness problem may be quickly found after solving the problem in question. Decision tree complexity The number of comparisons needed to solve the problem of size n, in a comparison-based model of computation such as a decision tree or algebraic decision ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Complexity Theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity, i.e., the amount of resources needed to solve them, such as time and storage. Other measures of complexity are also used, such as the amount of communication (used in communication complexity), the number of logic gate, gates in a circuit (used in circuit complexity) and the number of processors (used in parallel computing). O ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real RAM
In computing, especially computational geometry, a real RAM (random-access machine) is a mathematical model of a computer that can compute with exact real numbers instead of the binary fixed-point or floating-point numbers used by most actual computers. The real RAM was formulated by Michael Ian Shamos in his 1978 Ph.D. dissertation. Model The "RAM" part of the real RAM model name stands for "random-access machine". This is a model of computing that resembles a simplified version of a standard computer architecture. It consists of a stored program, a computer memory unit consisting of an array of cells, and a central processing unit with a bounded number of registers. Each memory cell or register can store a real number. Under the control of the program, the real RAM can transfer real numbers between memory and registers, and perform arithmetic operations on the values stored in the registers. The allowed operations typically include addition, subtraction, multiplication, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
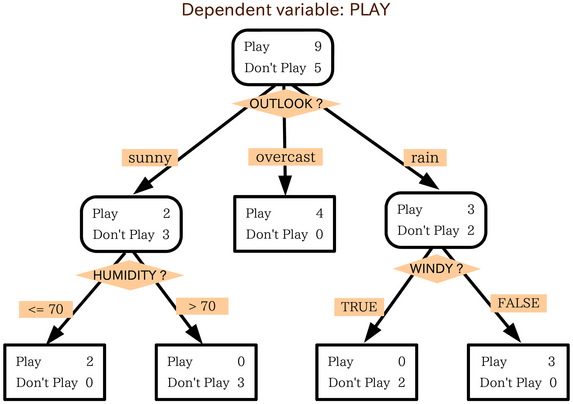
Decision Tree Model
In computational complexity theory, the decision tree model is the model of computation in which an algorithm can be considered to be a decision tree, i.e. a sequence of ''queries'' or ''tests'' that are done adaptively, so the outcome of previous tests can influence the tests performed next. Typically, these tests have a small number of outcomes (such as a yes–no question) and can be performed quickly (say, with unit computational cost), so the worst-case time complexity of an algorithm in the decision tree model corresponds to the depth of the corresponding tree. This notion of computational complexity of a problem or an algorithm in the decision tree model is called its decision tree complexity or query complexity. Decision tree models are instrumental in establishing lower bounds for the complexity of certain classes of computational problems and algorithms. Several variants of decision tree models have been introduced, depending on the computational model and type of quer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Misra–Gries Heavy Hitters Algorithm
Misra and Gries defined the ''heavy-hitters problem'' (though they did not introduce the term ''heavy-hitters'') and described the first algorithm for it in the paper ''Finding repeated elements''. Their algorithm extends the Boyer-Moore majority finding algorithm in a significant way. One version of the heavy-hitters problem is as follows: Given is a bag of elements and an integer . Find the values that occur more than times in . The Misra-Gries algorithm solves the problem by making two passes over the values in , while storing at most values from and their number of occurrences during the course of the algorithm. Misra-Gries is one of the earliest streaming algorithms, and it is described below in those terms in section #Summaries. Misra–Gries algorithm A bag is like a set in which the same value may occur multiple times. Assume that a bag is available as an array of elements. In the abstract description of the algorithm, we treat and its segments also as bags. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Computing
''Theory of Computing'' is a peer-reviewed open access scientific journal covering theoretical computer science. The journal was established in 2005 and is published by the Department of Computer Science of the University of Chicago. The editor-in-chief is László Babai László "Laci" Babai (born July 20, 1950, in Budapest) a fellow of the American Academy of Arts and Sciences, and won the Knuth Prize. Babai was an invited speaker at the International Congresses of Mathematicians in Kyoto (1990), Zürich (199 ... (University of Chicago). External links * Academic journals established in 2005 Creative Commons Attribution-licensed journals Computer science journals University of Chicago {{compu-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symposium On Foundations Of Computer Science
The IEEE Annual Symposium on Foundations of Computer Science (FOCS) is an academic conference in the field of theoretical computer science. FOCS is sponsored by the IEEE Computer Society. As writes, FOCS and its annual Association for Computing Machinery counterpart STOC (the Symposium on Theory of Computing) are considered the two top conferences in theoretical computer science, considered broadly: they “are forums for some of the best work throughout theory of computing that promote breadth among theory of computing researchers and help to keep the community together.” includes regular attendance at FOCS and STOC as one of several defining characteristics of theoretical computer scientists. Awards The Knuth Prize for outstanding contributions to theoretical computer science is presented alternately at FOCS and STOC. Works of the highest quality presented at the conference are awarded the Best Paper Award. In addition, the Machtey Award is presented to the best studen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SIAM Journal On Computing
The ''SIAM Journal on Computing'' is a scientific journal focusing on the mathematical and formal aspects of computer science. It is published by the Society for Industrial and Applied Mathematics (SIAM). Although its official ISO abbreviation is ''SIAM J. Comput.'', its publisher and contributors frequently use the shorter abbreviation ''SICOMP''. SICOMP typically hosts the special issues of the IEEE Annual Symposium on Foundations of Computer Science (FOCS) and the Annual ACM Symposium on Theory of Computing (STOC), where about 15% of papers published in FOCS and STOC each year are invited to these special issues. For example, Volume 48 contains 11 out of 85 papers published in FOCS 2016. References External linksSIAM Journal on Computing on |
Andris Ambainis
Andris Ambainis (born 18 January 1975) is a Latvian computer scientist active in the fields of quantum information theory and quantum computing. Education and career Ambainis has held past positions at the Institute for Advanced Study at Princeton, New Jersey and the Institute for Quantum Computing at the University of Waterloo. He is currently a professor in the Faculty of Computing at the University of Latvia. He received a Bachelors (1996), Masters (1997), and Doctorate (1997) in Computer Science from the University of Latvia, as well as a PhD (2001) from the University of California, Berkeley.Andris Ambainis' page at the . Contributions ...
|
Quantum Algorithm
In quantum computing, a quantum algorithm is an algorithm that runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical (or non-quantum) algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer. Although all classical algorithms can also be performed on a quantum computer, the term quantum algorithm is generally reserved for algorithms that seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition or quantum entanglement. Problems that are undecidable using classical computers remain undecidable using quantum computers. What makes quantum algorithms interesting is that they might be able to solve some problems fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing Machine
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algorithm. The machine operates on an infinite memory tape divided into discrete mathematics, discrete cells, each of which can hold a single symbol drawn from a finite set of symbols called the Alphabet (formal languages), alphabet of the machine. It has a "head" that, at any point in the machine's operation, is positioned over one of these cells, and a "state" selected from a finite set of states. At each step of its operation, the head reads the symbol in its cell. Then, based on the symbol and the machine's own present state, the machine writes a symbol into the same cell, and moves the head one step to the left or the right, or halts the computation. The choice of which replacement symbol to write, which direction to move the head, and whet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |