|
Electron Tomography
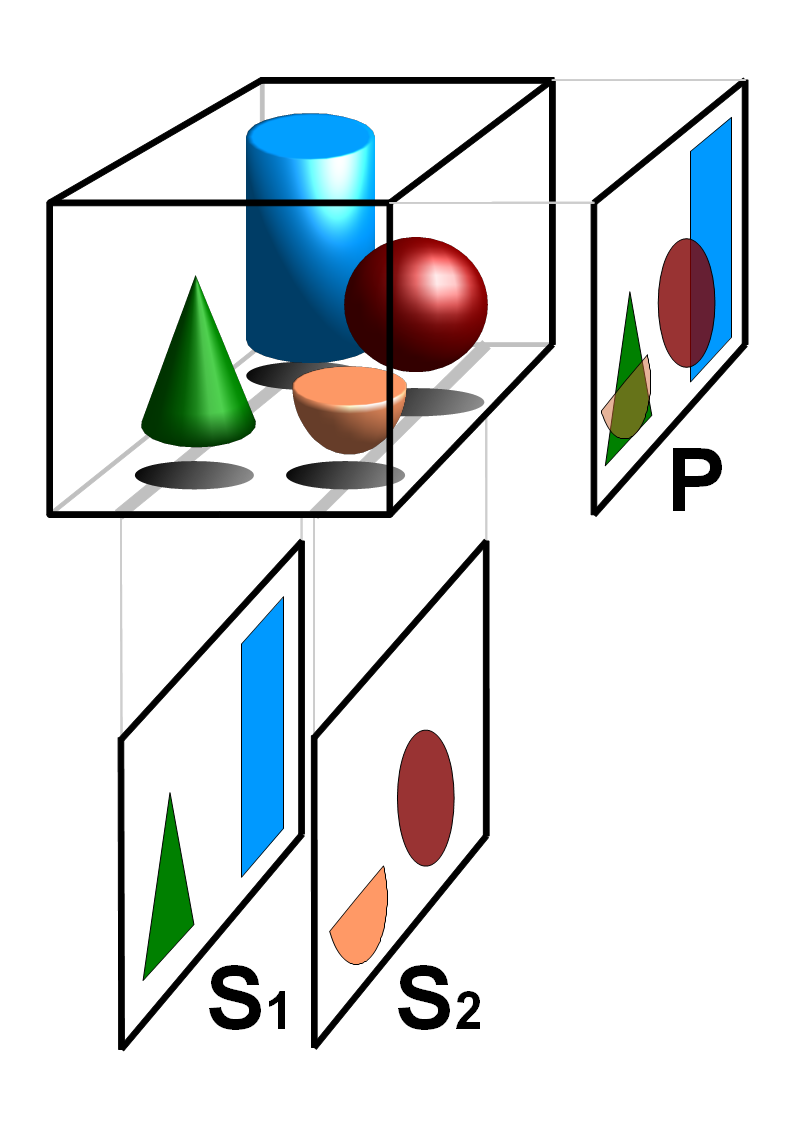
Electron tomography (ET) is a tomography technique for obtaining detailed 3D structures of sub-cellular, macro-molecular, or materials specimens. Electron tomography is an extension of traditional transmission electron microscopy and uses a transmission electron microscope to collect the data. In the process, a beam of electrons is passed through the sample at incremental degrees of rotation around the center of the target sample. This information is collected and used to assemble a three-dimensional image of the target. For biological applications, the typical resolution of ET systems are in the 5–20 nm range, suitable for examining supra-molecular multi-protein structures, although not the secondary and tertiary structure of an individual protein or polypeptide. Recently, atomic resolution in 3D electron tomography reconstructions has been demonstrated. BF-TEM and ADF-STEM tomography In the field of biology, bright-field transmission electron microscopy (BF-TEM) and high-res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Materials Science
Materials science is an interdisciplinary field of researching and discovering materials. Materials engineering is an engineering field of finding uses for materials in other fields and industries. The intellectual origins of materials science stem from the Age of Enlightenment, when researchers began to use analytical thinking from chemistry, physics, and engineering to understand ancient, phenomenological observations in metallurgy and mineralogy. Materials science still incorporates elements of physics, chemistry, and engineering. As such, the field was long considered by academic institutions as a sub-field of these related fields. Beginning in the 1940s, materials science began to be more widely recognized as a specific and distinct field of science and engineering, and major technical universities around the world created dedicated schools for its study. Materials scientists emphasize understanding how the history of a material (''processing'') influences its struc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Energy Loss Spectroscopy
Electron energy loss spectroscopy (EELS) is a form of electron microscopy in which a material is exposed to a beam of electrons with a known, narrow range of kinetic energies. Some of the electrons will undergo inelastic scattering, which means that they lose energy and have their paths slightly and randomly deflected. The amount of energy loss can be measured via an electron spectrometer and interpreted in terms of what caused the energy loss. Inelastic interactions include phonon excitations, inter- and intra- band transitions, plasmon excitations, inner shell ionizations, and Cherenkov radiation. The inner-shell ionizations are particularly useful for detecting the elemental components of a material. For example, one might find that a larger-than-expected number of electrons comes through the material with 285 eV less energy than they had when they entered the material. This is approximately the amount of energy needed to remove an inner-shell electron from a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fast Fourier Transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by Matrix decomposition, factorizing the DFT matrix into a product of Sparse matrix, sparse (mostly zero) factors. As a result, it manages to reduce the Computational complexity theory, complexity of computing the DFT from O(n^2), which arises if one simply applies the definition of DFT, to O(n \log n), where is the data size. The difference in speed can be enormous, especially for long data sets where may be in the thousands or millions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Reconstruction Technique
frame, Animated sequence of reconstruction steps, one iteration. The algebraic reconstruction technique (ART) is an iterative reconstruction technique used in computed tomography. It reconstructs an image from a series of angular projections (a sinogram). Gordon, Bender and Herman first showed its use in image reconstruction; whereas the method is known as Kaczmarz method in numerical linear algebra. An advantage of ART over other reconstruction methods (such as filtered backprojection) is that it is relatively easy to incorporate prior knowledge into the reconstruction process. ART can be considered as an iterative solver of a system of linear equations A x = b , where: : A is a sparse m \times n matrix whose values represent the relative contribution of each output pixel to different points in the sinogram ( m being the number of individual values in the sinogram, and n being the number of output pixels); : x represents the pixels in the generated (output) imag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative Reconstruction
Iterative reconstruction refers to Iteration, iterative algorithms used to reconstruct 2D and 3D reconstruction, 3D images in certain Digital imaging, imaging techniques. For example, in computed tomography an image must be reconstructed from projections of an object. Here, iterative reconstruction techniques are usually a better, but computationally more expensive alternative to the common filtered back projection (FBP) method, which directly calculates the image in a single reconstruction step.Herman, G. T.Fundamentals of computerized tomography: Image reconstruction from projection 2nd edition, Springer, 2009 In recent research works, scientists have shown that extremely fast computations and massive parallelism is possible for iterative reconstruction, which makes iterative reconstruction practical for commercialization. Basic concepts The reconstruction of an image from the acquired data is an inverse problem. Often, it is not possible to exactly solve the inverse problem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. In mathematics and computer science, iteration (along with the related technique of recursion) is a standard element of algorithms. Mathematics In mathematics, iteration may refer to the process of iterating a function, i.e. applying a function repeatedly, using the output from one iteration as the input to the next. Iteration of apparently simple functions can produce complex behaviors and difficult problems – for examples, see the Collatz conjecture and juggler sequences. Another use of iteration in mathematics is in iterative methods which are used to produce approximate numerical solutions to certain mathematical problems. Newton's method is an example of an iterative method. Manual calculation of a number's square root is a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cryogenic Electron Microscopy
Cryogenic electron microscopy (cryo-EM) is a transmission electron microscopy technique applied to samples cooled to cryogenic temperatures. For biological specimens, the structure is preserved by embedding in an environment of vitreous ice. An aqueous sample solution is applied to a grid-mesh and plunge-frozen in liquid ethane or a mixture of liquid ethane and propane. While development of the technique began in the 1970s, recent advances in detector technology and software algorithms have allowed for the determination of biomolecular structures at near-atomic resolution. This has attracted wide attention to the approach as an alternative to X-ray crystallography or NMR spectroscopy in the structural biology field. In 2017, the Nobel Prize in Chemistry was awarded to Jacques Dubochet, Joachim Frank, and Richard Henderson "for developing cryo-electron microscopy for the high-resolution structure determination of biomolecules in solution." '' Nature Methods'' also named cryo- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Twinning
Crystal twinning occurs when two or more adjacent crystals of the same mineral are oriented so that they share some of the same crystal lattice points in a symmetrical manner. The result is an intergrowth of two separate crystals that are tightly bonded to each other. The surface along which the lattice points are shared in twinned crystals is called a composition surface or twin plane. Crystallographers classify twinned crystals by a number of twin laws, which are specific to the crystal structure. The type of twinning can be a diagnostic tool in mineral identification. There are three main types of twinning. The first is growth twinning which can occur both in very large and very small particles. The second is transformation twinning, where there is a change in the crystal structure. The third is deformation twinning, in which twinning develops in a crystal in response to a shear stress, and is an important mechanism for permanent shape changes in a crystal. Definition T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dislocation
In materials science, a dislocation or Taylor's dislocation is a linear crystallographic defect or irregularity within a crystal structure that contains an abrupt change in the arrangement of atoms. The movement of dislocations allow atoms to slide over each other at low stress levels and is known as ''glide'' or Slip (materials science), slip. The crystalline order is restored on either side of a ''glide dislocation'' but the atoms on one side have moved by one position. The crystalline order is not fully restored with a ''partial dislocation''. A dislocation defines the boundary between ''slipped'' and ''unslipped'' regions of material and as a result, must either form a complete loop, intersect other dislocations or defects, or extend to the edges of the crystal. A dislocation can be characterised by the distance and direction of movement it causes to atoms which is defined by the Burgers vector. Plasticity (physics), Plastic deformation of a material occurs by the creation and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grain Boundary
In materials science, a grain boundary is the interface between two grains, or crystallites, in a polycrystalline material. Grain boundaries are two-dimensional defects in the crystal structure, and tend to decrease the electrical and thermal conductivity of the material. Most grain boundaries are preferred sites for the onset of corrosion and for the precipitation of new phases from the solid. They are also important to many of the mechanisms of creep. On the other hand, grain boundaries disrupt the motion of dislocations through a material, so reducing crystallite size is a common way to improve mechanical strength, as described by the Hall–Petch relationship. High and low angle boundaries It is convenient to categorize grain boundaries according to the extent of misorientation between the two grains. ''Low-angle grain boundaries'' (''LAGB'') or ''subgrain boundaries'' are those with a misorientation less than about 15 degrees. Generally speaking they are composed of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |