|
Dodecahedra
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Poinsot polyhedron, regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The #Pyritohedron, pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the #Tetartoid, tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyritohedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Poinsot polyhedron, regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The #Pyritohedron, pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the #Tetartoid, tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetartoid
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Dodecahedron
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals). It is represented by the Schläfli symbol . Dimensions If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the regular dodecahedron at all vertices) is :r_u = a\frac \left(1 + \sqrt\right) \approx 1.401\,258\,538 \cdot a and the radius of an inscribed sphere (tangent to each of the regular dodecahedron's faces) is :r_i = a\frac \sqrt \approx 1.113\,516\,364 \cdot a while the midradius, which touches the middle of each edge, is :r_m = a\frac \left(3 +\sqrt\right) \approx 1.309\,016\,994 \cdot a These quantities may also be expressed as :r_u = a\, \frac \phi :r_i = a\, \frac :r_m = a\, \frac where ''ϕ'' is the golden rat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Dodecahedron
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals). It is represented by the Schläfli symbol . Dimensions If the edge length of a regular dodecahedron is a, the radius of a circumscribed sphere (one that touches the regular dodecahedron at all vertices) is :r_u = a\frac \left(1 + \sqrt\right) \approx 1.401\,258\,538 \cdot a and the radius of an inscribed sphere (tangent to each of the regular dodecahedron's faces) is :r_i = a\frac \sqrt \approx 1.113\,516\,364 \cdot a while the midradius, which touches the middle of each edge, is :r_m = a\frac \left(3 +\sqrt\right) \approx 1.309\,016\,994 \cdot a These quantities may also be expressed as :r_u = a\, \frac \phi :r_i = a\, \frac :r_m = a\, \frac where ''ϕ'' is the golden rat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space-filling Polyhedra
In geometry, a honeycomb is a ''space filling'' or ''close packing'' of polyhedral or higher-dimensional ''cells'', so that there are no gaps. It is an example of the more general mathematical ''tiling'' or ''tessellation'' in any number of dimensions. Its dimension can be clarified as ''n''-honeycomb for a honeycomb of ''n''-dimensional space. Honeycombs are usually constructed in ordinary Euclidean ("flat") space. They may also be constructed in non-Euclidean spaces, such as hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space. Classification There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered. The simplest honeycombs to build are formed from stacked layers or ''slabs'' of prisms based on some tessellations of the plane. In particula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
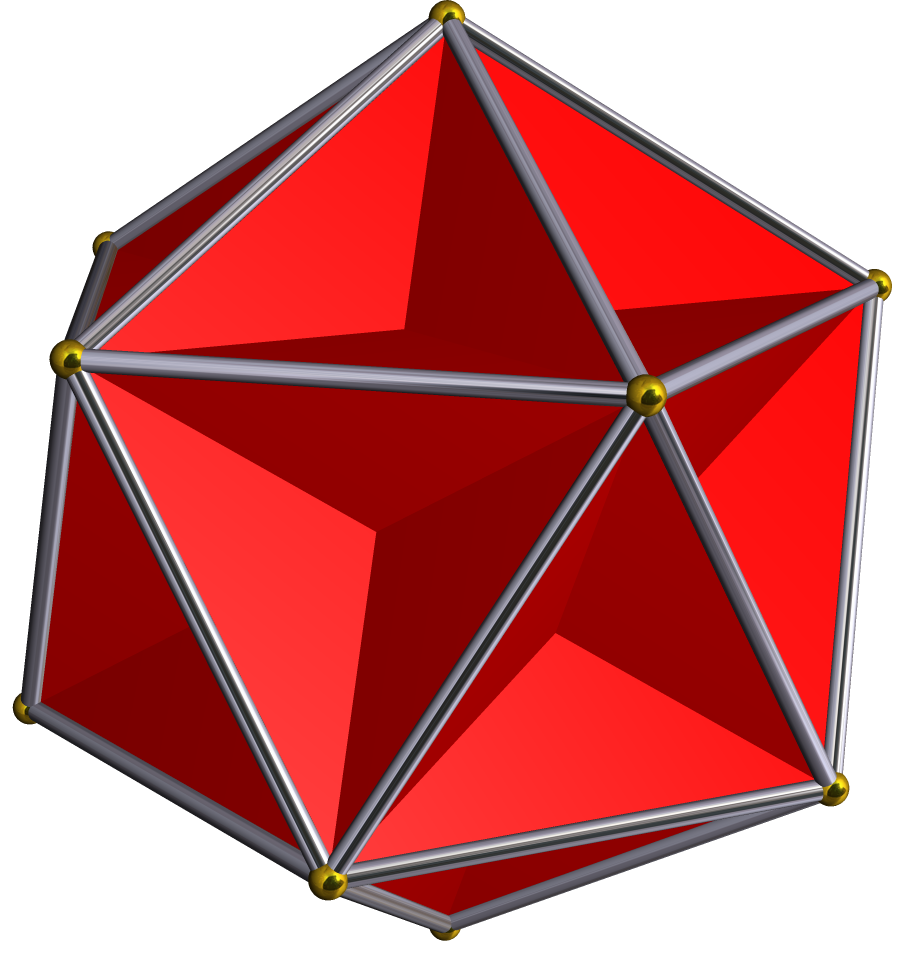
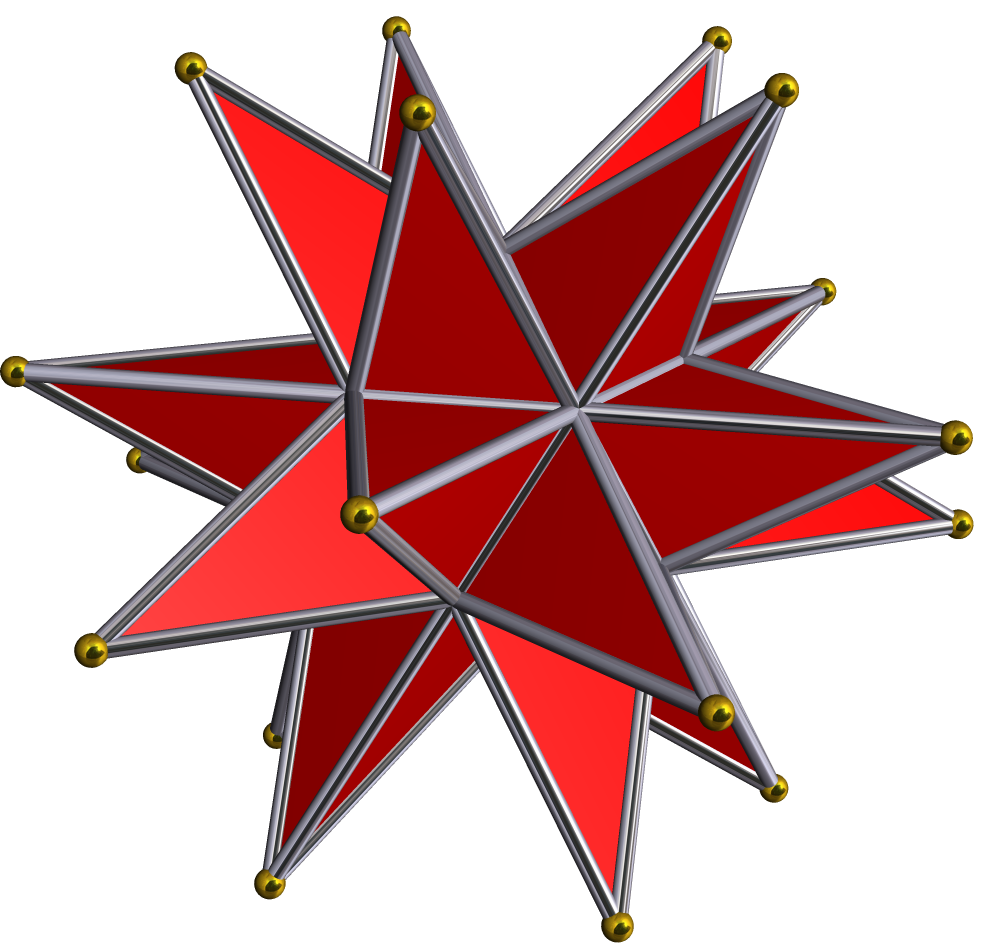
Kepler–Poinsot Polyhedron
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures. They can all be seen as three-dimensional analogues of the pentagram in one way or another. Characteristics Non-convexity These figures have pentagrams (star pentagons) as faces or vertex figures. The small and great stellated dodecahedron have nonconvex regular pentagram faces. The great dodecahedron and great icosahedron have convex polygonal faces, but pentagrammic vertex figures. In all cases, two faces can intersect along a line that is not an edge of either face, so that part of each face passes through the interior of the figure. Such lines of intersection are not part of the polyhedral structure and are sometimes called false edges. Likewise where three such lines intersect at a point that is not a corner of any face, these ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly times the short face-diagonal length; thus, the acute angles on each face measure arccos(), or approximately 70.53°. Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet correspond t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly times the short face-diagonal length; thus, the acute angles on each face measure arccos(), or approximately 70.53°. Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet correspond t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Dodecahedron
In geometry, the elongated dodecahedron, extended rhombic dodecahedron, rhombo-hexagonal dodecahedron or hexarhombic dodecahedron is a convex dodecahedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism. Parallelohedron Along with the rhombic dodecahedron, it is a space-filling polyhedron, one of the five types of parallelohedron identified by Evgraf Fedorov that tile space face-to-face by translations. It has 5 sets of parallel edges, called zones or belts. : Tessellation * It can tesselate all space by translations. * It is the Wigner–Seitz cell for certain body-centered tetragonal lattices. This is related to the rhombic dodecahedral honeycomb with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a square tiling with the rhombi projected into squares. Variat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombo-hexagonal Dodecahedron
In geometry, the elongated dodecahedron, extended rhombic dodecahedron, rhombo-hexagonal dodecahedron or hexarhombic dodecahedron is a convex dodecahedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism. Parallelohedron Along with the rhombic dodecahedron, it is a space-filling polyhedron, one of the five types of parallelohedron identified by Evgraf Fedorov that tile space face-to-face by translations. It has 5 sets of parallel edges, called zones or belts. : Tessellation * It can tesselate all space by translations. * It is the Wigner–Seitz cell for certain body-centered tetragonal lattices. This is related to the rhombic dodecahedral honeycomb with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a square tiling with the rhombi projected into squares. Variat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombo-hexagonal Dodecahedron
In geometry, the elongated dodecahedron, extended rhombic dodecahedron, rhombo-hexagonal dodecahedron or hexarhombic dodecahedron is a convex dodecahedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism. Parallelohedron Along with the rhombic dodecahedron, it is a space-filling polyhedron, one of the five types of parallelohedron identified by Evgraf Fedorov that tile space face-to-face by translations. It has 5 sets of parallel edges, called zones or belts. : Tessellation * It can tesselate all space by translations. * It is the Wigner–Seitz cell for certain body-centered tetragonal lattices. This is related to the rhombic dodecahedral honeycomb with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a square tiling with the rhombi projected into squares. Variat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |