|
Discrete Chebyshev Polynomials
In mathematics, discrete Chebyshev polynomials, or Gram polynomials, are a type of discrete orthogonal polynomials used in approximation theory, introduced by Pafnuty Chebyshev and rediscovered by Gram. They were later found to be applicable to various algebraic properties of spin angular momentum. Elementary Definition The discrete Chebyshev polynomial t^N_n(x) is a polynomial of degree ''n'' in ''x'', for n = 0, 1, 2,\ldots, N -1, constructed such that two polynomials of unequal degree are orthogonal with respect to the weight function w(x) = \sum_^ \delta(x-r), with \delta(\cdot) being the Dirac delta function. That is, \int_^ t^N_n(x) t^N_m (x) w(x) \, dx = 0 \quad \text \quad n \ne m . The integral on the left is actually a sum because of the delta function, and we have, \sum_^ t^N_n(r) t^N_m (r) = 0 \quad \text\quad n \ne m. Thus, even though t^N_n(x) is a polynomial in x, only its values at a discrete set of points, x = 0, 1, 2, \ldots, N-1 are of any significance. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Orthogonal Polynomials
In mathematics, a sequence of discrete orthogonal polynomials is a sequence of polynomials that are pairwise orthogonal with respect to a discrete measure. Examples include the discrete Chebyshev polynomials, Charlier polynomials, Krawtchouk polynomials, Meixner polynomials, dual Hahn polynomials, Hahn polynomials, and Racah polynomials. If the measure has finite support, then the corresponding sequence of discrete orthogonal polynomials has only a finite number of elements. The Racah polynomials give an example of this. Definition Consider a discrete measure \mu on some set S=\ with weight function \omega(x). A family of orthogonal polynomials \ is called discrete, if they are orthogonal with respect to \omega (resp. \mu), i.e. :\sum\limits_ p_n(x)p_m(x)\omega(x)=\kappa_n\delta_, where \delta_ is the Kronecker delta. Remark Any discrete measure is of the form : \mu = \sum_ a_i \delta_, so one can define a weight function by \omega(s_i) = a_i. Listeratur *{{Citation , last ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-norm
In mathematics, particularly in functional analysis, a seminorm is a vector space norm that need not be positive definite. Seminorms are intimately connected with convex sets: every seminorm is the Minkowski functional of some absorbing disk and, conversely, the Minkowski functional of any such set is a seminorm. A topological vector space is locally convex if and only if its topology is induced by a family of seminorms. Definition Let X be a vector space over either the real numbers \R or the complex numbers \Complex. A real-valued function p : X \to \R is called a if it satisfies the following two conditions: # Subadditivity/Triangle inequality: p(x + y) \leq p(x) + p(y) for all x, y \in X. # Absolute homogeneity: p(s x) =, s, p(x) for all x \in X and all scalars s. These two conditions imply that p(0) = 0If z \in X denotes the zero vector in X while 0 denote the zero scalar, then absolute homogeneity implies that p(z) = p(0 z) = , 0, p(z) = 0 p(z) = 0. \blacksquare and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wigner D-matrix
The Wigner D-matrix is a unitary matrix in an irreducible representation of the groups SU(2) and SO(3). It was introduced in 1927 by Eugene Wigner, and plays a fundamental role in the quantum mechanical theory of angular momentum. The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotors. The letter stands for ''Darstellung'', which means "representation" in German. Definition of the Wigner D-matrix Let be generators of the Lie algebra of SU(2) and SO(3). In quantum mechanics, these three operators are the components of a vector operator known as ''angular momentum''. Examples are the angular momentum of an electron in an atom, electronic spin, and the angular momentum of a rigid rotor. In all cases, the three operators satisfy the following commutation relations, : _x,J_y= i J_z,\quad _z,J_x= i J_y,\quad _y,J_z= i J_x, where ''i'' is the purely imaginary number and Planck's constant has been set equal to one. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
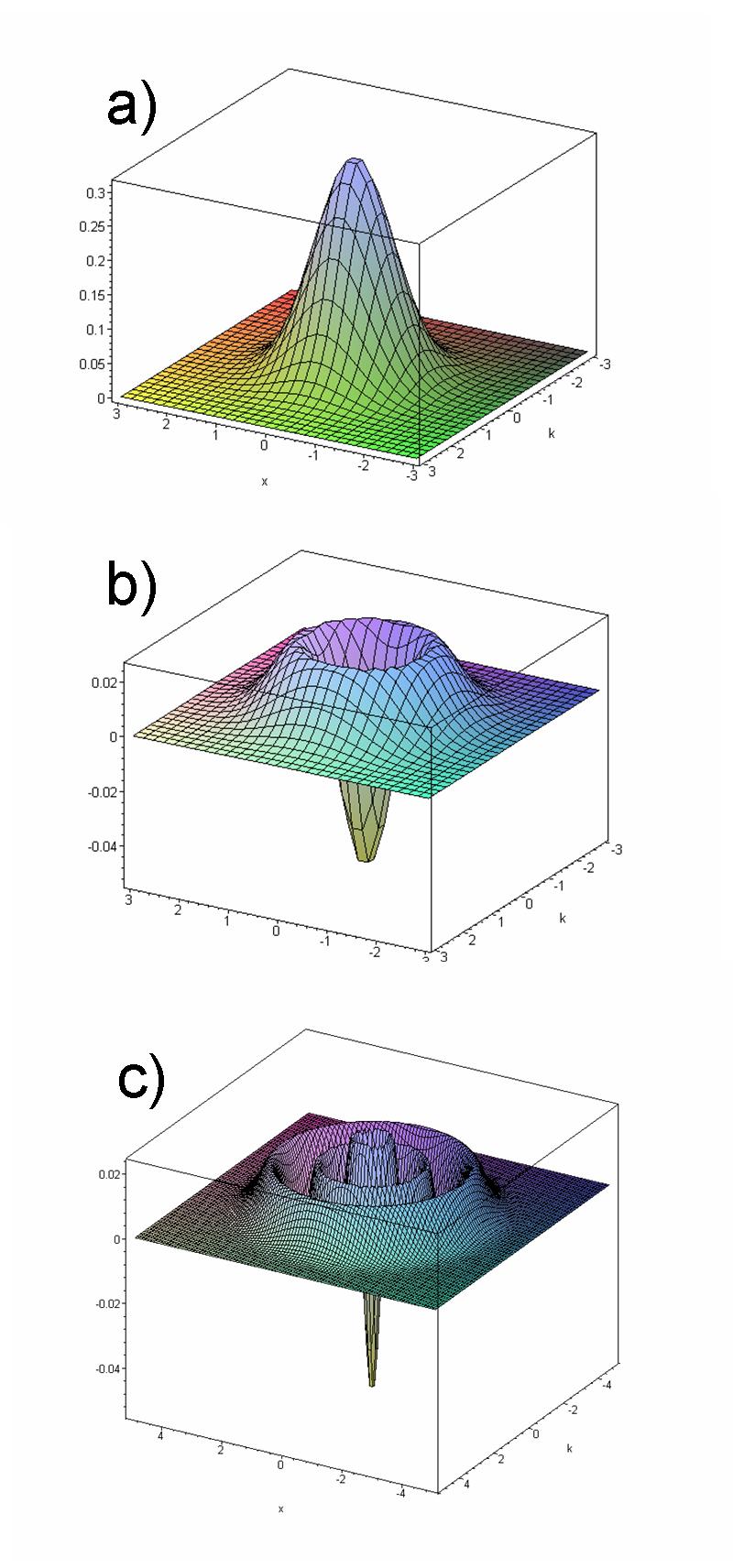
Wigner Quasiprobability Distribution
The Wigner quasiprobability distribution (also called the Wigner function or the Wigner–Ville distribution, after Eugene Wigner and Jean-André Ville) is a quasiprobability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics. The goal was to link the wavefunction that appears in Schrödinger's equation to a probability distribution in phase space. It is a generating function for all spatial autocorrelation functions of a given quantum-mechanical wavefunction . Thus, it maps on the quantum density matrix in the map between real phase-space functions and Hermitian operators introduced by Hermann Weyl in 1927, in a context related to representation theory in mathematics (see Weyl quantization). In effect, it is the Wigner–Weyl transform of the density matrix, so the realization of that operator in phase space. It was later rederived by Jean Ville in 1948 as a quadratic (in signal) representation of the local ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
EPR Paradox
EPR may refer to: Science and technology * EPR (nuclear reactor), European Pressurised-Water Reactor * EPR paradox (Einstein–Podolsky–Rosen paradox), in physics * Earth potential rise, in electrical engineering * East Pacific Rise, a mid-oceanic ridge * Electron paramagnetic resonance * Engine pressure ratio,of a jet engine * Ethylene propylene rubber * Yevpatoria RT-70 radio telescope (Evpatoria planetary radar) * Bernays–Schönfinkel class or effectively propositional, in mathematical logic * Endpoint references in Web addressing * Ethnic Power Relations, dataset of ethnic groups * ePrivacy Regulation (ePR), proposal for the regulation of various privacy-related topics, mostly in relation to electronic communications within the European Union Medicine * Enhanced permeability and retention effect, a controversial concept in cancer research * Emergency Preservation and Resuscitation, a medical procedure * Electronic patient record Environment * UNECE Environmental Perform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Bohm
David Joseph Bohm (; 20 December 1917 – 27 October 1992) was an American-Brazilian-British scientist who has been described as one of the most significant theoretical physicists of the 20th centuryPeat 1997, pp. 316-317 and who contributed unorthodox ideas to quantum theory, neuropsychology and the philosophy of mind. Among his many contributions to physics is his causal and deterministic interpretation of quantum theory, now known as De Broglie–Bohm theory. Bohm advanced the view that quantum physics meant that the old Cartesian model of reality—that there are two kinds of substance, the mental and the physical, that somehow interact—was too limited. To complement it, he developed a mathematical and physical theory of "implicate" and "explicate" order.David Bohm: ''Wholeness and the Implicate Order'', Routledge, 1980 (). He also believed that the brain, at the cellular level, works according to the mathematics of some quantum effects, and postulated that thought is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Approximation Theory
The ''Journal of Approximation Theory'' is "devoted to advances in pure and applied approximation theory and related areas." References External links ''Journal of Approximation Theory'' web site''Journal of Approximation Theory'' home page at Elsevier Mathematics journals Approximation theory Publications established in 1968 Elsevier academic journals English-language journals Monthly journals {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Vector
In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat"). The term ''direction vector'', commonly denoted as d, is used to describe a unit vector being used to represent spatial direction and relative direction. 2D spatial directions are numerically equivalent to points on the unit circle and spatial directions in 3D are equivalent to a point on the unit sphere. The normalized vector û of a non-zero vector u is the unit vector in the direction of u, i.e., :\mathbf = \frac where , u, is the norm (or length) of u. The term ''normalized vector'' is sometimes used as a synonym for ''unit vector''. Unit vectors are often chosen to form the basis of a vector space, and every vector in the space may be written as a linear combination of unit vectors. Orthogonal coordinates Cartesian coordinates Unit vectors may be us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leading Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves variables, they may also be called parameters. For example, the polynomial 2x^2-x+3 has coefficients 2, −1, and 3, and the powers of the variable x in the polynomial ax^2+bx+c have coefficient parameters a, b, and c. The constant coefficient is the coefficient not attached to variables in an expression. For example, the constant coefficients of the expressions above are the number 3 and the parameter ''c'', respectively. The coefficient attached to the highest degree of the variable in a polynomial is referred to as the leading coefficient. For example, in the expressions above, the leading coefficients are 2 and ''a'', respectively. Terminology and definition In mathematics, a coefficient is a multiplicative factor in some term of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indexed Family
In mathematics, a family, or indexed family, is informally a collection of objects, each associated with an index from some index set. For example, a ''family of real numbers, indexed by the set of integers'' is a collection of real numbers, where a given function selects one real number for each integer (possibly the same). More formally, an indexed family is a mathematical function together with its domain I and image X. (that is, indexed families and mathematical functions are technically identical, just point of views are different.) Often the elements of the set X are referred to as making up the family. In this view, indexed families are interpreted as collections of indexed elements instead of functions. The set I is called the ''index set'' of the family, and X is the ''indexed set''. Sequences are one type of families indexed by natural numbers. In general, the index set I is not restricted to be countable. For example, one could consider an uncountable family of sub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Theory
In mathematics, approximation theory is concerned with how function (mathematics), functions can best be approximation, approximated with simpler functions, and with quantitative property, quantitatively characterization (mathematics), characterizing the approximation error, errors introduced thereby. Note that what is meant by ''best'' and ''simpler'' will depend on the application. A closely related topic is the approximation of functions by generalized Fourier series, that is, approximations based upon summation of a series of terms based upon orthogonal polynomials. One problem of particular interest is that of approximating a function in a computer mathematical library, using operations that can be performed on the computer or calculator (e.g. addition and multiplication), such that the result is as close to the actual function as possible. This is typically done with polynomial or Rational function, rational (ratio of polynomials) approximations. The objective is to make t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |