|
Dimensionality Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable (hard to control or deal with). Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Approaches can also be divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an interme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intrinsic Dimension
The intrinsic dimension for a data set can be thought of as the number of variables needed in a minimal representation of the data. Similarly, in signal processing of multidimensional signals, the intrinsic dimension of the signal describes how many variables are needed to generate a good approximation of the signal. When estimating intrinsic dimension, however, a slightly broader definition based on manifold dimension is often used, where a representation in the intrinsic dimension does only need to exist locally. Such intrinsic dimension estimation methods can thus handle data sets with different intrinsic dimensions in different parts of the data set. This is often referred to as local intrinsic dimensionality. The intrinsic dimension can be used as a lower bound of what dimension it is possible to compress a data set into through dimension reduction, but it can also be used as a measure of the complexity of the data set or signal. For a data set or signal of ''N'' variables, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Classification
In statistics, classification is the problem of identifying which of a set of categories (sub-populations) an observation (or observations) belongs to. Examples are assigning a given email to the "spam" or "non-spam" class, and assigning a diagnosis to a given patient based on observed characteristics of the patient (sex, blood pressure, presence or absence of certain symptoms, etc.). Often, the individual observations are analyzed into a set of quantifiable properties, known variously as explanatory variables or ''features''. These properties may variously be categorical (e.g. "A", "B", "AB" or "O", for blood type), ordinal (e.g. "large", "medium" or "small"), integer-valued (e.g. the number of occurrences of a particular word in an email) or real-valued (e.g. a measurement of blood pressure). Other classifiers work by comparing observations to previous observations by means of a similarity or distance function. An algorithm that implements classification, especially in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-negative Matrix Factorization
Non-negative matrix factorization (NMF or NNMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix is factorized into (usually) two matrices and , with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms or muscular activity, non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically. NMF finds applications in such fields as astronomy, computer vision, document clustering, missing data imputation, chemometrics, audio signal processing, recommender systems, and bioinformatics. History In chemometrics non-negative matrix factorization has a long history under the name "self modeling curve resolution". In this framework the vectors in the right matrix are continuous cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MIT Press
The MIT Press is a university press affiliated with the Massachusetts Institute of Technology (MIT) in Cambridge, Massachusetts (United States). It was established in 1962. History The MIT Press traces its origins back to 1926 when MIT published under its own name a lecture series entitled ''Problems of Atomic Dynamics'' given by the visiting German physicist and later Nobel Prize winner, Max Born. Six years later, MIT's publishing operations were first formally instituted by the creation of an imprint called Technology Press in 1932. This imprint was founded by James R. Killian, Jr., at the time editor of MIT's alumni magazine and later to become MIT president. Technology Press published eight titles independently, then in 1937 entered into an arrangement with John Wiley & Sons in which Wiley took over marketing and editorial responsibilities. In 1962 the association with Wiley came to an end after a further 125 titles had been published. The press acquired its modern nam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nature (journal)
''Nature'' is a British weekly scientific journal founded and based in London, England. As a multidisciplinary publication, ''Nature'' features peer-reviewed research from a variety of academic disciplines, mainly in science and technology. It has core editorial offices across the United States, continental Europe, and Asia under the international scientific publishing company Springer Nature. ''Nature'' was one of the world's most cited scientific journals by the Science Edition of the 2019 '' Journal Citation Reports'' (with an ascribed impact factor of 42.778), making it one of the world's most-read and most prestigious academic journals. , it claimed an online readership of about three million unique readers per month. Founded in autumn 1869, ''Nature'' was first circulated by Norman Lockyer and Alexander Macmillan as a public forum for scientific innovations. The mid-20th century facilitated an editorial expansion for the journal; ''Nature'' redoubled its efforts in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation And Dependence
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (that is, the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation. A distinction must be made between (1) the covariance of two ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
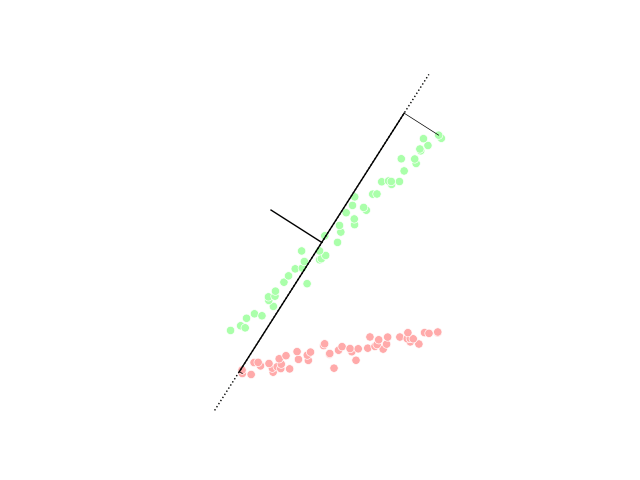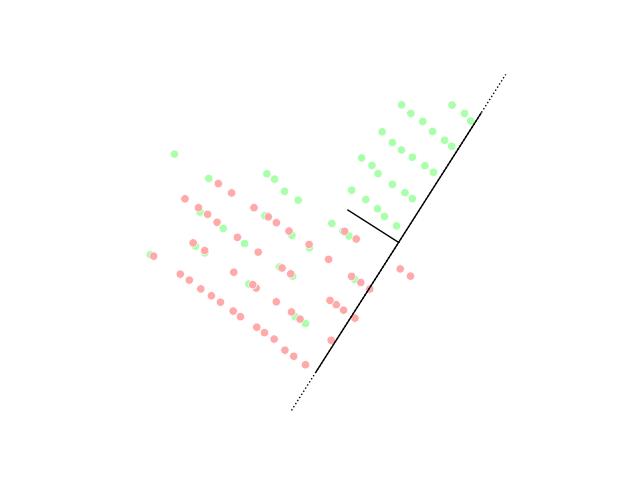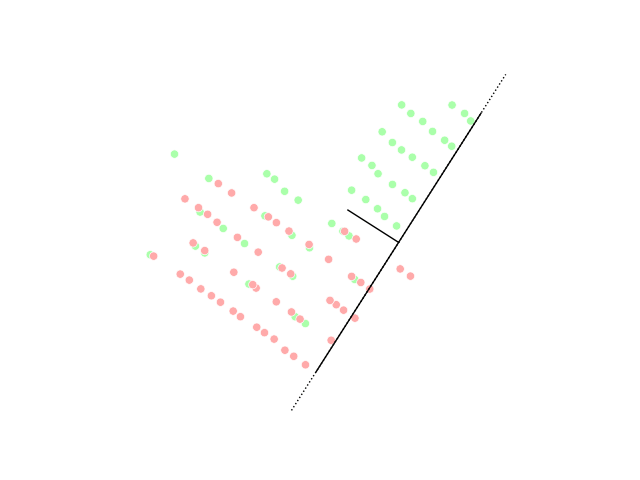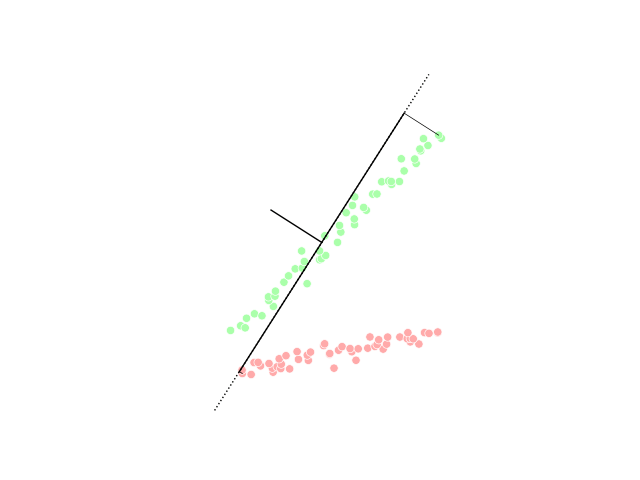
PCA Projection Illustration
PCA may refer to: Medicine and biology * Patient-controlled analgesia * Plate count agar in microbiology * Polymerase cycling assembly, for large DNA oligonucleotides * Posterior cerebral artery * Posterior cortical atrophy, a form of dementia * Protein-fragment complementation assay, to identify protein–protein interactions * Protocatechuic acid, a phenolic acid. * Personal Care Assistant, also known as unlicensed assistive personnel * Procainamide Military and government * EU-Armenia Partnership and Cooperation Agreement (PCA agreement between Armenia and the EU) * Parks Canada Agency * Partnership and Cooperation Agreement (EU) * Permanent change of assignment in US armed forces Organizations Business * Packaging Corporation of America * Peanut Corporation of America, former company * Pennsylvania Central Airlines 1936-1948 Education * Pacific Coast Academy, fictional school in TV series '' Zoey 101'' * Parents and citizens associations for schools in Austr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
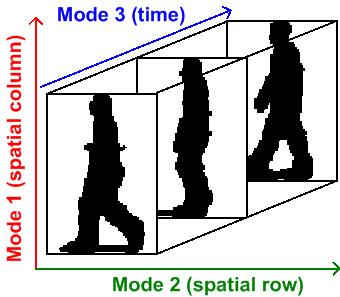
Multilinear Subspace Learning
Multilinear subspace learning is an approach to dimensionality reduction.M. A. O. Vasilescu, D. Terzopoulos (2003"Multilinear Subspace Analysis of Image Ensembles" "Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’03), Madison, WI, June, 2003"M. A. O. Vasilescu, D. Terzopoulos (2002"Multilinear Analysis of Image Ensembles: TensorFaces" Proc. 7th European Conference on Computer Vision (ECCV'02), Copenhagen, Denmark, May, 2002M. A. O. Vasilescu,(2002"Human Motion Signatures: Analysis, Synthesis, Recognition" "Proceedings of International Conference on Pattern Recognition (ICPR 2002), Vol. 3, Quebec City, Canada, Aug, 2002, 456–460." Dimensionality reduction can be performed on a data tensor that contains a collection of observations have been vectorized, or observations that are treated as matrices and concatenated into a data tensor.X. He, D. Cai, P. NiyogiTensor subspace analysis in: Advances in Neural Information Processing Systemsc 18 (N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Representation
In mathematics, the tensor representations of the general linear group are those that are obtained by taking finitely many tensor products of the fundamental representation and its dual. The irreducible factors of such a representation are also called tensor representations, and can be obtained by applying Schur functors (associated to Young tableaux). These coincide with the rational representations of the general linear group. More generally, a matrix group is any subgroup of the general linear group. A tensor representation of a matrix group is any representation that is contained in a tensor representation of the general linear group. For example, the orthogonal group O(''n'') admits a tensor representation on the space of all trace-free symmetric tensors of order two. For orthogonal groups, the tensor representations are contrasted with the spin representations. The classical groups, like the symplectic group In mathematics, the name symplectic group can refer to two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |