|
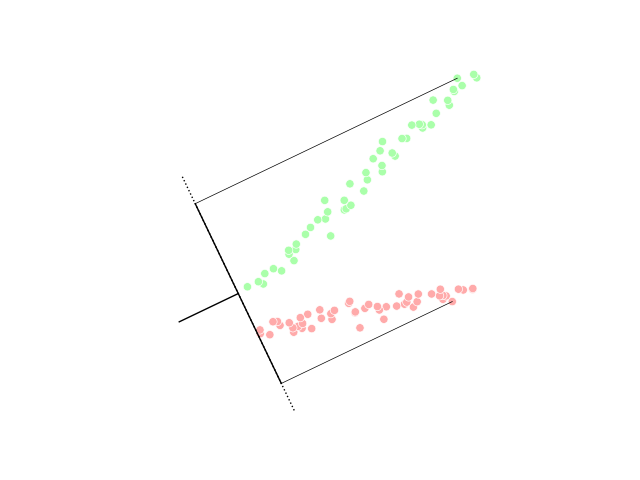
Decision Boundary
__NOTOC__ In a statistical-classification problem with two classes, a decision boundary or decision surface is a hypersurface that partitions the underlying vector space into two sets, one for each class. The classifier will classify all the points on one side of the decision boundary as belonging to one class and all those on the other side as belonging to the other class. A decision boundary is the region of a problem space in which the output label of a classifier is ambiguous. If the decision surface is a hyperplane, then the classification problem is linear, and the classes are linearly separable. Decision boundaries are not always clear cut. That is, the transition from one class in the feature space to another is not discontinuous, but gradual. This effect is common in fuzzy logic based classification algorithms, where membership in one class or another is ambiguous. Decision boundaries can be approximations of optimal stopping boundaries. The decision boundary is the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Classification
In statistics, classification is the problem of identifying which of a set of categories (sub-populations) an observation (or observations) belongs to. Examples are assigning a given email to the "spam" or "non-spam" class, and assigning a diagnosis to a given patient based on observed characteristics of the patient (sex, blood pressure, presence or absence of certain symptoms, etc.). Often, the individual observations are analyzed into a set of quantifiable properties, known variously as explanatory variables or ''features''. These properties may variously be categorical (e.g. "A", "B", "AB" or "O", for blood type), ordinal (e.g. "large", "medium" or "small"), integer-valued (e.g. the number of occurrences of a particular word in an email) or real-valued (e.g. a measurement of blood pressure). Other classifiers work by comparing observations to previous observations by means of a similarity or distance function. An algorithm that implements classification, especially in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", i.e. that the space not exclude any ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topologic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classification Algorithms
Classification is a process related to categorization, the process in which ideas and objects are recognized, differentiated and understood. Classification is the grouping of related facts into classes. It may also refer to: Business, organizations, and economics * Classification of customers, for marketing (as in Master data management) or for profitability (e.g. by Activity-based costing) * Classified information, as in legal or government documentation * Job classification, as in job analysis * Standard Industrial Classification, economic activities Mathematics * Attribute-value system, a basic knowledge representation framework * Classification theorems in mathematics * Mathematical classification, grouping mathematical objects based on a property that all those objects share * Statistical classification, identifying to which of a set of categories a new observation belongs, on the basis of a training set of data Media * Classification (literature), a figure of speech li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperplane Separation Theorem
In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in ''n''-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint. The hyperplane separation theorem is due to Hermann Minkowski. The Hahn–Banach separation theorem generalizes the result to topological vector spaces. A related result is the supporting hyperplane theorem. In the context of support-vector machines, the ''optimally separating hyperplane'' or ''maximum-margin hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant Function
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical independent variables and a continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regression and probit regression are more similar to LDA than ANOVA is, as they also explain a categorical var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Trick
In machine learning, kernel machines are a class of algorithms for pattern analysis, whose best known member is the support-vector machine (SVM). The general task of pattern analysis is to find and study general types of relations (for example clusters, rankings, principal components, correlations, classifications) in datasets. For many algorithms that solve these tasks, the data in raw representation have to be explicitly transformed into feature vector representations via a user-specified ''feature map'': in contrast, kernel methods require only a user-specified ''kernel'', i.e., a similarity function over all pairs of data points computed using Inner products. The feature map in kernel machines is infinite dimensional but only requires a finite dimensional matrix from user-input according to the Representer theorem. Kernel machines are slow to compute for datasets larger than a couple of thousand examples without parallel processing. Kernel methods owe their name to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum-margin Hyperplane
In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in ''n''-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint. The hyperplane separation theorem is due to Hermann Minkowski. The Hahn–Banach separation theorem generalizes the result to topological vector spaces. A related result is the supporting hyperplane theorem. In the context of support-vector machines, the ''optimally separating hyperplane'' or ''maximum-margin hype ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Support Vector Machine
In machine learning, support vector machines (SVMs, also support vector networks) are supervised learning models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories by Vladimir Vapnik with colleagues (Boser et al., 1992, Guyon et al., 1993, Cortes and Vapnik, 1995, Vapnik et al., 1997) SVMs are one of the most robust prediction methods, being based on statistical learning frameworks or VC theory proposed by Vapnik (1982, 1995) and Chervonenkis (1974). Given a set of training examples, each marked as belonging to one of two categories, an SVM training algorithm builds a model that assigns new examples to one category or the other, making it a non- probabilistic binary linear classifier (although methods such as Platt scaling exist to use SVM in a probabilistic classification setting). SVM maps training examples to points in space so as to maximise the width of the gap between the two categories. New ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Universal Approximation Theorem
In the mathematical theory of artificial neural networks, universal approximation theorems are results that establish the density of an algorithmically generated class of functions within a given function space of interest. Typically, these results concern the approximation capabilities of the feedforward architecture on the space of continuous functions between two Euclidean spaces, and the approximation is with respect to the compact convergence topology. However, there are also a variety of results between non-Euclidean spaces and other commonly used architectures and, more generally, algorithmically generated sets of functions, such as the convolutional neural network (CNN) architecture, radial basis-functions, or neural networks with specific properties. Most universal approximation theorems can be parsed into two classes. The first quantifies the approximation capabilities of neural networks with an arbitrary number of artificial neurons ("''arbitrary width''" case) and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypersurface
In geometry, a hypersurface is a generalization of the concepts of hyperplane, plane curve, and surface. A hypersurface is a manifold or an algebraic variety of dimension , which is embedded in an ambient space of dimension , generally a Euclidean space, an affine space or a projective space. Hypersurfaces share, with surfaces in a three-dimensional space, the property of being defined by a single implicit equation, at least locally (near every point), and sometimes globally. A hypersurface in a (Euclidean, affine, or projective) space of dimension two is a plane curve. In a space of dimension three, it is a surface. For example, the equation :x_1^2+x_2^2+\cdots+x_n^2-1=0 defines an algebraic hypersurface of dimension in the Euclidean space of dimension . This hypersurface is also a smooth manifold, and is called a hypersphere or an -sphere. Smooth hypersurface A hypersurface that is a smooth manifold is called a ''smooth hypersurface''. In , a smooth hypersurface is orienta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |