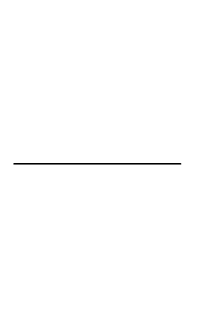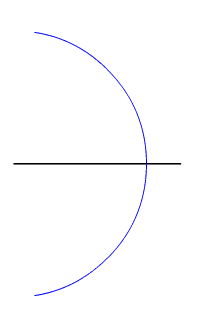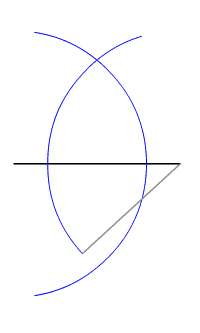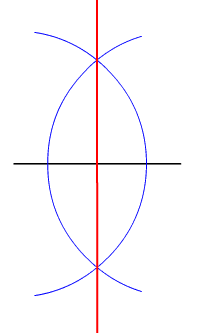|
Dynamical Symmetry Breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry. Overview By definition, spontaneous symmetry breaking requires the existence of physical laws (e.g. quantum mechanics) which are invariant under a symmetry transformation (such as translation or rotation), so that any pair of outcomes differing only by that transformation have the same probability distribution. For example if measurements of an observable at any two different positions have the same probability distribution, the observable has translational symmetry. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spontaneous Process
In thermodynamics, a spontaneous process is a process which occurs without any external input to the system. A more technical definition is the time-evolution of a system in which it releases free energy and it moves to a lower, more thermodynamically stable energy state (closer to thermodynamic equilibrium). 0 and Δ''H'' 0 and Δ''H'' > 0, the process will be spontaneous at high temperatures and non-spontaneous at low temperatures. * When Δ''S'' \left, \Delta S_\text{system}\ In many processes, the increase in entropy of the surroundings is accomplished via heat transfer from the system to the surroundings (i.e. an exothermic process). See also * Endergonic reaction reactions which are not spontaneous at standard temperature, pressure, and concentrations. * Diffusion Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetization
In classical electromagnetism, magnetization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material. Movement within this field is described by direction and is either Axial or Diametric. The origin of the magnetic moments responsible for magnetization can be either microscopic electric currents resulting from the motion of electrons in atoms, or the spin of the electrons or the nuclei. Net magnetization results from the response of a material to an external magnetic field. Paramagnetic materials have a weak induced magnetization in a magnetic field, which disappears when the magnetic field is removed. Ferromagnetic and ferrimagnetic materials have strong magnetization in a magnetic field, and can be ''magnetized'' to have magnetization in the absence of an external field, becoming a permanent magnet. Magnetization is not necessarily uniform within a material, but may vary between different points. Magnetizatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spontaneous Symmetry Breaking (explanatory Diagram)
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry. When the system goes to one of those vacuum solutions, the symmetry is broken for perturbations around that vacuum even though the entire Lagrangian retains that symmetry. Overview By definition, spontaneous symmetry breaking requires the existence of physical laws (e.g. quantum mechanics) which are invariant under a symmetry transformation (such as translation or rotation), so that any pair of outcomes differing only by that transformation have the same probability distribution. For example if measurements of an observable at any two different positions have the same probability distribution, the observable has translational symmetry. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equidistant
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal. In two-dimensional Euclidean geometry, the locus of points equidistant from two given (different) points is their perpendicular bisector. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in n-dimensional space the locus of points equidistant from two points in ''n''-space is an (''n''−1)-space. For a triangle the circumcentre is a point equidistant from each of the three vertices. Every non-degenerate triangle has such a point. This result can be generalised to cyclic polygons: the circumcentre is equidistant from each of the vertices. Likewise, the incentre of a triangle or any other tangential polygon is equidistant from the points of tangency of the polygon's sides with the circle. Every point on a perpendicular bisector of the side of a triangle or other polygon is equidist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Potential
In classical mechanics, the gravitational potential at a location is equal to the work (energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance. In mathematics, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies. Potential energy The gravitational potential (''V'') at a location is the gravitational potential energy (''U'') at that location per unit mass: V = \frac, where ''m'' is the mass of the object. Potential energy is equal (in magnitude, but negative) to the w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilibrium Point
In mathematics, specifically in differential equations, an equilibrium point is a constant solution to a differential equation. Formal definition The point \tilde\in \mathbb^n is an equilibrium point for the differential equation :\frac = \mathbf(t,\mathbf) if \mathbf(t,\tilde)=\mathbf for all t. Similarly, the point \tilde\in \mathbb^n is an equilibrium point (or fixed point) for the difference equation :\mathbf_ = \mathbf(k,\mathbf_k) if \mathbf(k,\tilde)= \tilde for k=0,1,2,\ldots. Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances), by finding th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotational Velocity
In physics, angular velocity or rotational velocity ( or ), also known as angular frequency vector,(UP1) is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an object rotates or revolves relative to a point or axis). The magnitude of the pseudovector represents the ''angular speed'', the rate at which the object rotates or revolves, and its direction is normal to the instantaneous plane of rotation or angular displacement. The orientation of angular velocity is conventionally specified by the right-hand rule.(EM1) There are two types of angular velocity. * Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. * Spin angular velocity refers to how fast a rigid body rotates with respect to its center of rotation and is independent of the choice of origin, in contrast to orbital angular ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. For a convex shape in the plane, the diameter is defined to be the largest distance that can be formed between two opposite parallel lines tangent to its boundary, and the is often defined to be the smallest such distance. Both quantities can be calculated efficiently using rotating calipers. For a curve of constant width such as the Reuleaux triangle, the width and diameter are the same because all ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection Cell
In the field of fluid dynamics, a convection cell is the phenomenon that occurs when density differences exist within a body of liquid or gas. These density differences result in rising and/or falling currents, which are the key characteristics of a convection cell. When a volume of fluid is heated, it expands and becomes less dense and thus more buoyant than the surrounding fluid. The colder, denser part of the fluid descends to settle below the warmer, less-dense fluid, and this causes the warmer fluid to rise. Such movement is called convection, and the moving body of liquid is referred to as a ''convection cell''. This particular type of convection, where a horizontal layer of fluid is heated from below, is known as Rayleigh–Bénard convection. Convection usually requires a gravitational field, but in microgravity experiments, thermal convection has been observed without gravitational effects. Fluids are generalized as materials that exhibit the property of flow; however, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid
In physics, a fluid is a liquid, gas, or other material that continuously deforms (''flows'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are substances which cannot resist any shear force applied to them. Although the term ''fluid'' generally includes both the liquid and gas phases, its definition varies among branches of science. Definitions of ''solid'' vary as well, and depending on field, some substances can be both fluid and solid. Viscoelastic fluids like Silly Putty appear to behave similar to a solid when a sudden force is applied. Substances with a very high viscosity such as pitch appear to behave like a solid (see pitch drop experiment) as well. In particle physics, the concept is extended to include fluidic matters other than liquids or gases. A fluid in medicine or biology refers any liquid constituent of the body (body fluid), whereas "liquid" is not used in this sense. Sometimes liquids given for flui ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electroweak
In particle physics, the electroweak interaction or electroweak force is the unified field theory, unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different aspects of the same force. Above the electroweak scale, unification energy, on the order of 246 GeV,The particular number 246 GeV is taken to be the vacuum expectation value v = (G_\text \sqrt)^ of the Higgs field (where G_\text is the Fermi coupling constant). they would merge into a single force. Thus, if the temperature is high enough – approximately 1015 Kelvin, K – then the electromagnetic force and weak force merge into a combined electroweak force. During the quark epoch (shortly after the Big Bang), the electroweak force split into the electromagnetic and weak force. It is thought that the required temperature of 1015 K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Friedmann–Lemaître–Robertson–Walker Metric
The Friedmann–Lemaître–Robertson–Walker (FLRW; ) metric is a metric based on the exact solution of Einstein's field equations of general relativity; it describes a homogeneous, isotropic, expanding (or otherwise, contracting) universe that is path-connected, but not necessarily simply connected. The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, the set of the four scientists – Alexander Friedmann, Georges Lemaître, Howard P. Robertson and Arthur Geoffrey Walker – are customarily grouped as Friedmann or Friedmann–Robertson–Walker (FRW) or Robertson–Walker (RW) or Friedmann–Lemaître (FL). This model is sometimes called the ''Standard Model'' of modern cosmology, although such a description is also associated with the further developed Lambda-CDM model. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)