|
Cycloid
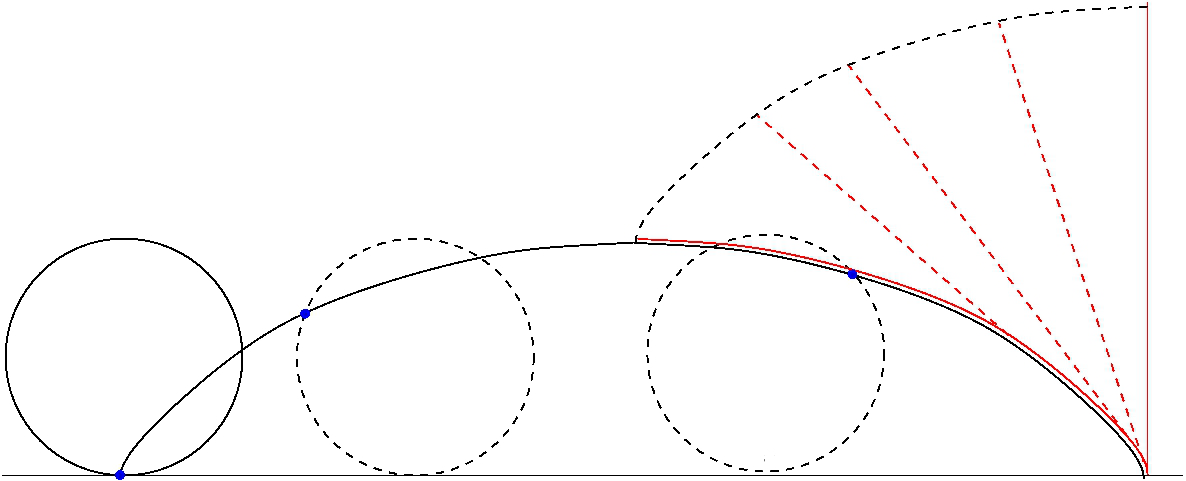
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician John Wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid F
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician John Wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tautochrone Curve
A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and chrono ''time'') is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to π times the square root of the radius (of the circle which generates the cycloid) over the acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid. The tautochrone problem The tautochrone problem, the attempt to identify this curve, was solved by Christiaan Huygens in 1659. He proved geometrically in his ''Horologium Oscillatorium'', originally published in 1673, that the curve is a cycloid. The cycloid is given by a point on a circle of radius r tracing a curve as the circle rolls along the x axis, as: \begin x &= r(\theta - \sin \theta) \\ y &= r(1 - \cos \theta), \end Huygens al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trochoid
In geometry, a trochoid () is a roulette curve formed by a circle rolling along a line. It is the curve traced out by a point fixed to a circle (where the point may be on, inside, or outside the circle) as it rolls along a straight line. If the point is on the circle, the trochoid is called ''common'' (also known as a cycloid); if the point is inside the circle, the trochoid is ''curtate''; and if the point is outside the circle, the trochoid is ''prolate''. The word "trochoid" was coined by Gilles de Roberval. Basic description As a circle of radius rolls without slipping along a line , the center moves parallel to , and every other point in the rotating plane rigidly attached to the circle traces the curve called the trochoid. Let . Parametric equations of the trochoid for which is the -axis are :\begin & x = a\theta - b \sin \theta \\ & y = a - b \cos \theta \end where is the variable angle through which the circle rolls. Curtate, common, prolate If lies inside the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cavalieri's Principle
In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows: * 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane. If every line parallel to these two lines intersects both regions in line segments of equal length, then the two regions have equal areas. * 3-dimensional case: Suppose two regions in three-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross-sections of equal area, then the two regions have equal volumes. Today Cavalieri's principle is seen as an early step towards integral calculus, and while it is used in some forms, such as its generalization in Fubini's theorem, results using Cavalieri's principle can often be shown more directly via integration. In the other direction, Cavalieri's principle grew out of the ancient Greek method of exhaustion, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rolling
Rolling is a type of motion that combines rotation (commonly, of an axially symmetric object) and translation of that object with respect to a surface (either one or the other moves), such that, if ideal conditions exist, the two are in contact with each other without sliding. Rolling where there is no sliding is referred to as ''pure rolling''. By definition, there is no sliding when there is a frame of reference in which all points of contact on the rolling object have the same velocity as their counterparts on the surface on which the object rolls; in particular, for a frame of reference in which the rolling plane is at rest (see animation), the instantaneous velocity of all the points of contact (e.g., a generating line segment of a cylinder) of the rolling object is zero. In practice, due to small deformations near the contact area, some sliding and energy dissipation occurs. Nevertheless, the resulting rolling resistance is much lower than sliding friction, and thus, roll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marin Mersenne
Marin Mersenne, OM (also known as Marinus Mersennus or ''le Père'' Mersenne; ; 8 September 1588 – 1 September 1648) was a French polymath whose works touched a wide variety of fields. He is perhaps best known today among mathematicians for Mersenne prime numbers, those which can be written in the form for some integer . He also developed Mersenne's laws, which describe the harmonics of a vibrating string (such as may be found on guitars and pianos), and his seminal work on music theory, ''Harmonie universelle'', for which he is referred to as the "father of acoustics". Mersenne, an ordained Catholic priest, had many contacts in the scientific world and has been called "the center of the world of science and mathematics during the first half of the 1600s" and, because of his ability to make connections between people and ideas, "the post-box of Europe". He was also a member of the Minim religious order and wrote and lectured on theology and philosophy. Life Mersenne was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rolling curve is a circle and the fixed curve is a line then the roulette is a trochoid. If, in this case, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
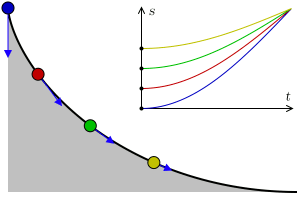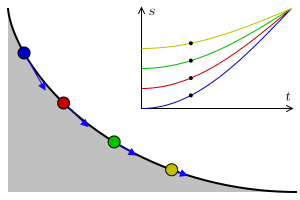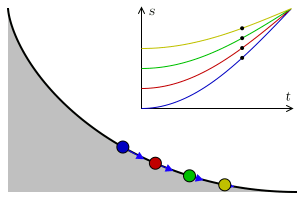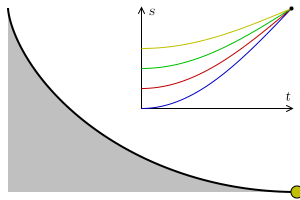
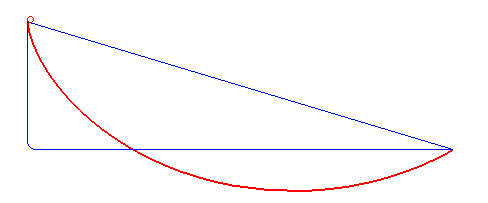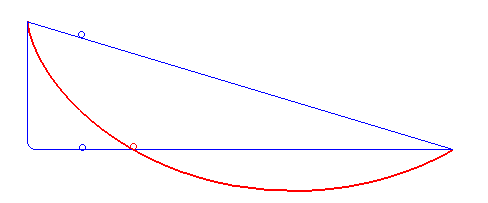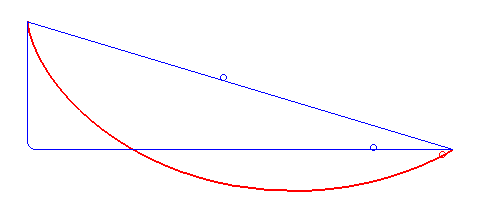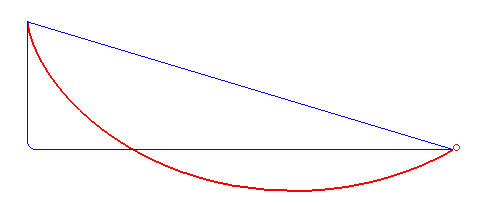
Brachistochrone Curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: Thomson Brooks/Cole, 2012. 640. Pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Siegmund Guenther
Sigmund or Siegmund may refer to: People * Sigmund (given name), list of people with the name Sigmund * Sigmund Freud, a pioneer of psychoanalysis Arts and entertainment *''Sigmund and the Sea Monsters, American 1970s TV series ;Fictional chatacters * Sigmund (also Siegmund), a hero in Norse mythology * Siegmund, a focal character in Richard Wagner's ''Die Walküre'' * Sigmund (comics), Doctor Sigmund, a Dutch comics character Others * , a cargo ship in service 1926-29 See also * Sigismund (other) Sigismund (variants: Sigmund, Siegmund) is a German proper name, meaning "protection through victory", from Old High German ''sigu'' "victory" + ''munt'' "hand, protection". Tacitus latinises it '' Segimundus''. There appears to be an older form of ... * Zygmunt, a given name {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642) was an Italian astronomer, physicist and engineer, sometimes described as a polymath. Commonly referred to as Galileo, his name was pronounced (, ). He was born in the city of Pisa, then part of the Duchy of Florence. Galileo has been called the "father" of observational astronomy, modern physics, the scientific method, and modern science. Galileo studied speed and velocity, gravity and free fall, the principle of relativity, inertia, projectile motion and also worked in applied science and technology, describing the properties of pendulums and "hydrostatic balances". He invented the thermoscope and various military compasses, and used the telescope for scientific observations of celestial objects. His contributions to observational astronomy include telescopic confirmation of the phases of Venus, observation of the four largest satellites of Jupiter, observation of Saturn's rings, and a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moritz Cantor
Moritz Benedikt Cantor (23 August 1829 – 10 April 1920) was a German historian of mathematics. Biography Cantor was born at Mannheim. He came from a Sephardi Jewish family that had emigrated to the Netherlands from Portugal Portugal, officially the Portuguese Republic ( pt, República Portuguesa, links=yes ), is a country whose mainland is located on the Iberian Peninsula of Southwestern Europe, and whose territory also includes the Atlantic archipelagos of ..., another branch of which had established itself in Russia. In his early youth, Moritz Cantor was not strong enough to go to school, and his parents decided to educate him at home. Later, however, he was admitted to an advanced class of the Gymnasium in Mannheim. From there he went to the University of Heidelberg in 1848, and soon after to the University of Göttingen, where he studied under Carl Friedrich Gauss, Gauss and Heinrich Martin Weber, Weber, and where Stern awakened in him a strong interest in histor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evangelista Torricelli
Evangelista Torricelli ( , also , ; 15 October 160825 October 1647) was an Italian physicist and mathematician, and a student of Galileo. He is best known for his invention of the barometer, but is also known for his advances in optics and work on the method of indivisibles. The Torr is also named after him. Biography Early life Torricelli was born on 15 October 1608 in Rome, the firstborn child of Gaspare Torricelli and Caterina Angetti. His family was from Faenza in the Province of Ravenna, then part of the Papal States. His father was a textile worker and the family was very poor. Seeing his talents, his parents sent him to be educated in Faenza, under the care of his uncle, Giacomo (James), a Camaldolese monk, who first ensured that his nephew was given a sound basic education. He then entered young Torricelli into a Jesuit College in 1624, possibly the one in Faenza itself, to study mathematics and philosophy until 1626, by which time his father, Gaspare, had died. The uncl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
