|
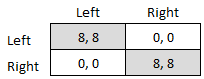
Coordination Problem
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-equilibrium combinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prisoner's Dilemma
The Prisoner's Dilemma is an example of a game analyzed in game theory. It is also a thought experiment that challenges two completely rational agents to a dilemma: cooperate with their partner for mutual reward, or betray their partner ("defect") for individual reward. This dilemma was originally framed by Merrill Flood and Melvin Dresher while working at RAND in 1950. Albert W. Tucker appropriated the game and formalized it by structuring the rewards in terms of prison sentences and named it "prisoner's dilemma". William Poundstone in his 1993 book ''Prisoner's Dilemma'' writes the following version:Two members of a criminal gang are arrested and imprisoned. Each prisoner is in solitary confinement with no means of speaking to or exchanging messages with the other. The police admit they don't have enough evidence to convict the pair on the principal charge. They plan to sentence both to two years in prison on a lesser charge. Simultaneously, the police offer each prisoner a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andreas Ortmann
Andreas Ortmann (born 28 January 1953 in Oerlinghausen, North Rhine-Westphalia, Germany) is a German-born economist and Professor of Experimental and Behavioural Economics at the UNSW Business School.Andreas Ortmann ''''. He is best known for his work on experimental methodology in social sciences, s and |
Stag Hunt
In game theory, the stag hunt, sometimes referred to as the assurance game, trust dilemma or common interest game, describes a conflict between safety and social cooperation. The stag hunt problem originated with philosopher Jean-Jacques Rousseau in his ''Discourse on Inequality''. In Rousseau's telling, two hunters must decide separately, and without the other knowing, whether to hunt a stag or a hare. However, both hunters know the only way to successfully hunt a stag is with the other's help. One hunter can catch a hare alone with less effort and less time, but it is worth far less than a stag and has much less meat. Rousseau therefore posits it would be much better for each hunter, acting individually, to give up total autonomy and minimal risk, which brings only the small reward of the hare. Instead, each hunter should separately choose the more ambitious and far more rewarding goal of getting the stag, thereby giving up some autonomy in exchange for the other hunter's coop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk Dominance
Risk dominance and payoff dominance are two related refinements of the Nash equilibrium (NE) solution concept in game theory, defined by John Harsanyi and Reinhard Selten. A Nash equilibrium is considered payoff dominant if it is Pareto superior to all other Nash equilibria in the game. When faced with a choice among equilibria, all players would agree on the payoff dominant equilibrium since it offers to each player at least as much payoff as the other Nash equilibria. Conversely, a Nash equilibrium is considered risk dominant if it has the largest basin of attraction (i.e. is less risky). This implies that the more uncertainty players have about the actions of the other player(s), the more likely they will choose the strategy corresponding to it. The payoff matrix in Figure 1 provides a simple two-player, two-strategy example of a game with two pure Nash equilibria. The strategy pair (Hunt, Hunt) is payoff dominant since payoffs are higher for both players compared to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fairness
Fairness or being fair can refer to: * Justice * The character in the award-nominated musical comedy '' A Theory of Justice: The Musical.'' * Equity (law), a legal principle allowing for the use of discretion and fairness when applying justice * Social justice, equality and solidarity in a society * Distributive justice, the perceived appropriateness of the distribution of goods, benefits, and other outcomes in a society, group, or organization (see also: teleology) * Procedural justice, the perceived appropriateness of rules or procedures used to allocate goods, benefits, and other outcomes (see also: deontology) * Interactional justice, the perceived appropriateness of interpersonal treatment * Environmental justice, the perceived appropriateness of the use or treatment of the environment or people via the environment, typically as a function of interpersonal or international relations * Fairness measure, metrics to quantify the fair distribution of resources * Perceptions a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Salience (neuroscience)
Salience (also called saliency) is that property by which some thing stands out. Salient events are an attentional mechanism by which organisms learn and survive; those organisms can focus their limited perceptual and cognitive resources on the pertinent (that is, salient) subset of the sensory data available to them. Saliency typically arises from contrasts between items and their neighborhood. They might be represented, for example, by a red dot surrounded by white dots, or by a flickering message indicator of an answering machine, or a loud noise in an otherwise quiet environment. Saliency detection is often studied in the context of the visual system, but similar mechanisms operate in other sensory systems. Just what is salient can be influenced by training: for example, for human subjects particular letters can become salient by training. There can be a sequence of necessary events, each of which has to be salient, in turn, in order for successful training in the sequence; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Payoff Dominance
Risk dominance and payoff dominance are two related refinements of the Nash equilibrium (NE) solution concept in game theory, defined by John Harsanyi and Reinhard Selten. A Nash equilibrium is considered payoff dominant if it is Pareto superior to all other Nash equilibria in the game. When faced with a choice among equilibria, all players would agree on the payoff dominant equilibrium since it offers to each player at least as much payoff as the other Nash equilibria. Conversely, a Nash equilibrium is considered risk dominant if it has the largest basin of attraction (i.e. is less risky). This implies that the more uncertainty players have about the actions of the other player(s), the more likely they will choose the strategy corresponding to it. The payoff matrix in Figure 1 provides a simple two-player, two-strategy example of a game with two pure Nash equilibria. The strategy pair (Hunt, Hunt) is payoff dominant since payoffs are higher for both players compared to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlated Equilibrium
In game theory, a correlated equilibrium is a solution concept that is more general than the well known Nash equilibrium. It was first discussed by mathematician Robert Aumann in 1974. The idea is that each player chooses their action according to their private observation of the value of the same public signal. A strategy assigns an action to every possible observation a player can make. If no player would want to deviate from their strategy (assuming the others also don't deviate), the distribution from which the signals are drawn is called a correlated equilibrium. Formal definition An N-player strategic game \displaystyle (N,A_i,u_i) is characterized by an action set A_i and utility function u_i for each player i. When player i chooses strategy a_i \in A_i and the remaining players choose a strategy profile described by the N-1-tuple a_, then player i's utility is \displaystyle u_i(a_i,a_). A ''strategy modification'' for player i is a function \phi_i\colon A_i \to A_i. That ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Aumann
Robert John Aumann (Hebrew name: , Yisrael Aumann; born June 8, 1930) is an Israeli-American mathematician, and a member of the United States National Academy of Sciences. He is a professor at the Center for the Study of Rationality in the Hebrew University of Jerusalem in Israel. He also holds a visiting position at Stony Brook University, and is one of the founding members of the Stony Brook Center for Game Theory. Aumann received the Nobel Memorial Prize in Economic Sciences in 2005 for his work on conflict and cooperation through game theory analysis. He shared the prize with Thomas Schelling. Early years Aumann was born in Frankfurt am Main, Germany, and fled to the United States with his family in 1938, two weeks before the Kristallnacht pogrom. He attended the Rabbi Jacob Joseph School, a yeshiva high school in New York City. Academic career Aumann graduated from the City College of New York in 1950 with a B.Sc. in mathematics. He received his M.Sc. in 1952, and his Ph.D. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolutionarily Stable Strategy
An evolutionarily stable strategy (ESS) is a strategy (or set of strategies) that is ''impermeable'' when adopted by a population in adaptation to a specific environment, that is to say it cannot be displaced by an alternative strategy (or set of strategies) which may be novel or initially rare. Introduced by John Maynard Smith and George R. Price in 1972/3, it is an important concept in behavioural ecology, evolutionary psychology, mathematical game theory and economics, with applications in other fields such as anthropology, philosophy and political science. In game-theoretical terms, an ESS is an equilibrium refinement of the Nash equilibrium, being a Nash equilibrium that is also "evolutionarily stable." Thus, once fixed in a population, natural selection alone is sufficient to prevent alternative (mutant) strategies from replacing it (although this does not preclude the possibility that a better strategy, or set of strategies, will emerge in response to selective pressures r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |