|
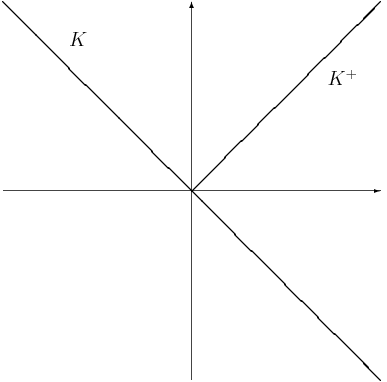
Consistent Pricing Process
A consistent pricing process (CPP) is any representation of ( frictionless) "prices" of assets in a market. It is a stochastic process in a filtered probability space (\Omega,\mathcal,\_^T,P) such that at time t the i^ component can be thought of as a price for the i^ asset. Mathematically, a CPP Z = (Z_t)_^T in a market with d-assets is an adapted process in \mathbb^d if ''Z'' is a martingale with respect to the physical probability measure P, and if Z_t \in K_t^+ \backslash \ at all times t such that K_t is the solvency cone for the market at time t. The CPP plays the role of an equivalent martingale measure in markets with transaction costs In economics and related disciplines, a transaction cost is a cost in making any economic trade when participating in a market. Oliver E. Williamson defines transaction costs as the costs of running an economic system of companies, and unlike produ .... In particular, there exists a 1-to-1 correspondence between the CPP Z and the EMM Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frictionless Market
Frictionless can refer to: * Frictionless market * Frictionless continuant * Frictionless sharing * Frictionless plane The frictionless plane is a concept from the writings of Galileo Galilei. In his 1638 '' The Two New Sciences'', Galileo presented a formula that predicted the motion of an object moving down an inclined plane. His formula was based upon his past e ... * Frictionless flow {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance. Applications and the study of phenomena have in turn inspired the proposal of new stochastic processes. Examples of such stochastic processes include the Wiener process or Brownian motion process, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filtered Probability Space
Filtration is a physical separation process that separates solid matter and fluid from a mixture using a ''filter medium'' that has a complex structure through which only the fluid can pass. Solid particles that cannot pass through the filter medium are described as ''oversize'' and the fluid that passes through is called the ''filtrate''. Oversize particles may form a filter cake on top of the filter and may also block the filter lattice, preventing the fluid phase from crossing the filter, known as ''blinding''. The size of the largest particles that can successfully pass through a filter is called the effective ''pore size'' of that filter. The separation of solid and fluid is imperfect; solids will be contaminated with some fluid and filtrate will contain fine particles (depending on the pore size, filter thickness and biological activity). Filtration occurs both in nature and in engineered systems; there are biological, geological, and industrial forms. Filtration is also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adapted Process
In the study of stochastic processes, an adapted process (also referred to as a non-anticipating or non-anticipative process) is one that cannot "see into the future". An informal interpretation is that ''X'' is adapted if and only if, for every realisation and every ''n'', ''Xn'' is known at time ''n''. The concept of an adapted process is essential, for instance, in the definition of the Itō integral, which only makes sense if the integrand is an adapted process. Definition Let * (\Omega, \mathcal, \mathbb) be a probability space; * I be an index set with a total order \leq (often, I is \mathbb, \mathbb_0, , T/math> or filtration of the sigma algebra \mathcal; * (S,\Sigma) be a measurable space, the ''state space''; * X: I \times \Omega \to S be a stochastic process. The process X is said to be adapted to the filtration \left(\mathcal_i\right)_ if the random variable X_i: \Omega \to S is a (\mathcal_i, \Sigma)-measurable function for each i \in I. Examples Consider a stochastic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martingale (probability Theory)
In probability theory, a martingale is a sequence of random variables (i.e., a stochastic process) for which, at a particular time, the conditional expectation of the next value in the sequence is equal to the present value, regardless of all prior values. History Originally, '' martingale'' referred to a class of betting strategies that was popular in 18th-century France. The simplest of these strategies was designed for a game in which the gambler wins their stake if a coin comes up heads and loses it if the coin comes up tails. The strategy had the gambler double their bet after every loss so that the first win would recover all previous losses plus win a profit equal to the original stake. As the gambler's wealth and available time jointly approach infinity, their probability of eventually flipping heads approaches 1, which makes the martingale betting strategy seem like a sure thing. However, the exponential growth of the bets eventually bankrupts its users due to f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as ''countable additivity''. The difference between a probability measure and the more general notion of measure (which includes concepts like area or volume) is that a probability measure must assign value 1 to the entire probability space. Intuitively, the additivity property says that the probability assigned to the union of two disjoint events by the measure should be the sum of the probabilities of the events; for example, the value assigned to "1 or 2" in a throw of a dice should be the sum of the values assigned to "1" and "2". Probability measures have applications in diverse fields, from physics to finance and biology. Definition The requirements for a function \mu to be a probability measure on a probability space are that: * \mu must return results in the unit interval , 1 returning 0 for the empty set and 1 for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solvency Cone
The solvency cone is a concept used in financial mathematics which models the possible trades in the Market (economics), financial market. This is of particular interest to markets with transaction costs. Specifically, it is the convex cone of portfolios that can be exchanged to portfolios of non-negative components (including paying of any transaction costs). Mathematical basis If given a bid-ask matrix \Pi for d assets such that \Pi = \left(\pi^\right)_ and m \leq d is the number of assets which with any non-negative quantity of them can be "discarded" (traditionally m = d), then the solvency cone K(\Pi) \subset \mathbb^d is the convex cone spanned by the unit vectors e^i, 1 \leq i \leq m and the vectors \pi^e^i-e^j, 1 \leq i,j \leq d. Definition A solvency cone K is any closed convex cone such that K \subseteq \mathbb^d and K \supseteq \mathbb^d_+. Uses A process of (random) solvency cones \left\_^T is a model of a financial market. This is sometimes called a market process. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalent Martingale Measure
In mathematical finance, a risk-neutral measure (also called an equilibrium measure, or ''equivalent martingale measure'') is a probability measure such that each share price is exactly equal to the discounted expectation of the share price under this measure. This is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market, a derivative's price is the discounted expected value of the future payoff under the unique risk-neutral measure. Such a measure exists if and only if the market is arbitrage-free. The easiest way to remember what the risk-neutral measure is, or to explain it to a probability generalist who might not know much about finance, is to realize that it is: # The probability measure of a transformed random variable. Typically this transformation is the utility function of the payoff. The risk-neutral measure would be the measure corresponding to an expectation of the payoff with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transaction Costs
In economics and related disciplines, a transaction cost is a cost in making any economic trade when participating in a market. Oliver E. Williamson defines transaction costs as the costs of running an economic system of companies, and unlike production costs, decision-makers determine strategies of companies by measuring transaction costs and production costs. Transaction costs are the total costs of making a transaction, including the cost of planning, deciding, changing plans, resolving disputes, and after-sales. Therefore, the transaction cost is one of the most significant factors in business operation and management. Oliver E. Williamson's ''Transaction Cost Economics'' popularized the concept of transaction costs. Douglass C. North argues that institutions, understood as the set of rules in a society, are key in the determination of transaction costs. In this sense, institutions that facilitate low transaction costs, boost economic growth.North, Douglass C. 1992. “Transac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-to-one Correspondence
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. There are no unpaired elements. In mathematical terms, a bijective function is a one-to-one (injective) and onto (surjective) mapping of a set ''X'' to a set ''Y''. The term ''one-to-one correspondence'' must not be confused with ''one-to-one function'' (an injective function; see figures). A bijection from the set ''X'' to the set ''Y'' has an inverse function from ''Y'' to ''X''. If ''X'' and ''Y'' are finite sets, then the existence of a bijection means they have the same number of elements. For infinite sets, the picture is more complicated, leading to the concept of cardinal number—a way to distinguish the various sizes of infinite sets. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Financial Risk Modeling
Financial risk modeling is the use of formal mathematical and econometric techniques to measure, monitor and control the market risk, credit risk, and operational risk on a firm's balance sheet, on a bank's trading book, or re a fund manager's portfolio value; see Financial risk management. Risk modeling is one of many subtasks within the broader area of financial modeling. Application Risk modeling uses a variety of techniques including market risk, value at risk (VaR), historical simulation (HS), or extreme value theory (EVT) in order to analyze a portfolio and make forecasts of the likely losses that would be incurred for a variety of risks. As above, such risks are typically grouped into credit risk, market risk, model risk, liquidity risk, and operational risk categories. Many large financial intermediary firms use risk modeling to help portfolio managers assess the amount of capital reserves to maintain, and to help guide their purchases and sales of various classes of f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |