|
Compare Instruction
In computer science, a relational operator is a programming language construct or operator that tests or defines some kind of relation between two entities. These include numerical equality (''e.g.'', ) and inequalities (''e.g.'', ). In programming languages that include a distinct boolean data type in their type system, like Pascal, Ada, or Java, these operators usually evaluate to true or false, depending on if the conditional relationship between the two operands holds or not. In languages such as C, relational operators return the integers 0 or 1, where 0 stands for false and any non-zero value stands for true. An expression created using a relational operator forms what is termed a ''relational expression'' or a ''condition''. Relational operators can be seen as special cases of logical predicates. Equality Usage Equality is used in many programming language constructs and data types. It is used to test if an element already exists in a set, or to access to a value th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Expressions
Conditional (if then) may refer to: *Causal conditional, if X then Y, where X is a cause of Y *Conditional probability, the probability of an event A given that another event B has occurred *Conditional proof, in logic: a proof that asserts a conditional, and proves that the antecedent leads to the consequent *Strict conditional, in philosophy, logic, and mathematics *Material conditional, in propositional calculus, or logical calculus in mathematics *Relevance conditional, in relevance logic *Conditional (computer programming), a statement or expression in computer programming languages *A conditional expression in computer programming languages such as ?: *Conditions in a contract Grammar and linguistics *Conditional mood (or conditional tense), a verb form in many languages *Conditional sentence, a sentence type used to refer to hypothetical situations and their consequences **Indicative conditional, a conditional sentence expressing "if A then B" in a natural language **Count ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (computer Science)
In computer science, a set is an abstract data type that can store unique values, without any particular order. It is a computer implementation of the mathematical concept of a finite set. Unlike most other collection types, rather than retrieving a specific element from a set, one typically tests a value for membership in a set. Some set data structures are designed for static or frozen sets that do not change after they are constructed. Static sets allow only query operations on their elements — such as checking whether a given value is in the set, or enumerating the values in some arbitrary order. Other variants, called dynamic or mutable sets, allow also the insertion and deletion of elements from the set. A multiset is a special kind of set in which an element can appear multiple times in the set. Type theory In type theory, sets are generally identified with their indicator function (characteristic function): accordingly, a set of values of type A may be denoted by 2^ o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floating-point Arithmetic
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can be represented as a base-ten floating-point number: 12.345 = \underbrace_\text \times \underbrace_\text\!\!\!\!\!\!^ In practice, most floating-point systems use base two, though base ten (decimal floating point) is also common. The term ''floating point'' refers to the fact that the number's radix point can "float" anywhere to the left, right, or between the significant digits of the number. This position is indicated by the exponent, so floating point can be considered a form of scientific notation. A floating-point system can be used to represent, with a fixed number of digits, numbers of very different orders of magnitude — such as the number of meters between galaxies or between protons in an atom. For this reason, floating-poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fraction (mathematics)
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A ''common'', ''vulgar'', or ''simple'' fraction (examples: \tfrac and \tfrac) consists of a numerator, displayed above a line (or before a slash like ), and a non-zero denominator, displayed below (or after) that line. Numerators and denominators are also used in fractions that are not ''common'', including compound fractions, complex fractions, and mixed numerals. In positive common fractions, the numerator and denominator are natural numbers. The numerator represents a number of equal parts, and the denominator indicates how many of those parts make up a unit or a whole. The denominator cannot be zero, because zero parts can never make up a whole. For example, in the fraction , the numerator 3 indicates that the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity (object-oriented Programming)
In object-oriented programming, object-oriented design and object-oriented analysis, the identity of an object is its being distinct from any other object, regardless of the values of the objects' properties. Having identity is a fundamental property of objects. This is closely related to the philosophical concept of identity. Identity and references A reference can be used to refer to an object with a specific identity. A reference contains the information that is necessary for the identity property to be realized in the programming language, and allows access to the object with the identity. A type of a target of a reference is a role. Typically, references are isomorphic to memory addresses. However, multiple such references can refer to the same object, if some form of address mapping is present ( virtual addresses / page tables / memory segments). Object identity is less useful as a semantic concept in environments or situations in which the structure of objects is not e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
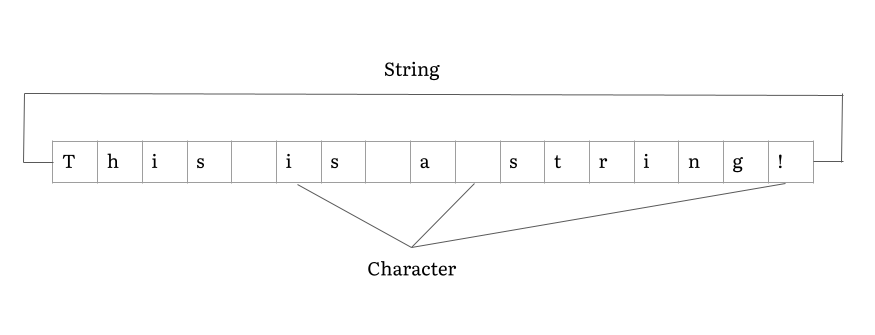
String (computer Science)
In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed (after creation). A string is generally considered as a data type and is often implemented as an array data structure of bytes (or words) that stores a sequence of elements, typically characters, using some character encoding. ''String'' may also denote more general arrays or other sequence (or list) data types and structures. Depending on the programming language and precise data type used, a variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears literally in source code, it is known as a string literal or an anonymous string. In formal languages, which are used in mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transitive Relation
In mathematics, a relation on a set is transitive if, for all elements , , in , whenever relates to and to , then also relates to . Each partial order as well as each equivalence relation needs to be transitive. Definition A homogeneous relation on the set is a ''transitive relation'' if, :for all , if and , then . Or in terms of first-order logic: :\forall a,b,c \in X: (aRb \wedge bRc) \Rightarrow aRc, where is the infix notation for . Examples As a non-mathematical example, the relation "is an ancestor of" is transitive. For example, if Amy is an ancestor of Becky, and Becky is an ancestor of Carrie, then Amy, too, is an ancestor of Carrie. On the other hand, "is the birth parent of" is not a transitive relation, because if Alice is the birth parent of Brenda, and Brenda is the birth parent of Claire, then this does not imply that Alice is the birth parent of Claire. What is more, it is antitransitive: Alice can ''never'' be the birth parent of Claire. "Is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and nature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflexive Relation
In mathematics, a binary relation ''R'' on a set ''X'' is reflexive if it relates every element of ''X'' to itself. An example of a reflexive relation is the relation " is equal to" on the set of real numbers, since every real number is equal to itself. A reflexive relation is said to have the reflexive property or is said to possess reflexivity. Along with symmetry and transitivity, reflexivity is one of three properties defining equivalence relations. Definitions Let R be a binary relation on a set X, which by definition is just a subset of X \times X. For any x, y \in X, the notation x R y means that (x, y) \in R while "not x R y" means that (x, y) \not\in R. The relation R is called if x R x for every x \in X or equivalently, if \operatorname_X \subseteq R where \operatorname_X := \ denotes the identity relation on X. The of R is the union R \cup \operatorname_X, which can equivalently be defined as the smallest (with respect to \subseteq) reflexive relation on X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reference (computer Science)
In computer programming, a reference is a value that enables a program to indirectly access a particular data, such as a variable's value or a record, in the computer's memory or in some other storage device. The reference is said to refer to the datum, and accessing the datum is called dereferencing the reference. A reference is distinct from the datum itself. A reference is an abstract data type and may be implemented in many ways. Typically, a reference refers to data stored in memory on a given system, and its internal value is the memory address of the data, i.e. a reference is implemented as a pointer. For this reason a reference is often said to "point to" the data. Other implementations include an offset (difference) between the datum's address and some fixed "base" address, an index, unique key, or identifier used in a lookup operation into an array or table, an operating system handle, a physical address on a storage device, or a network address such as a URL. For ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity (mathematics)
In mathematics, an identity is an equality relating one mathematical expression ''A'' to another mathematical expression ''B'', such that ''A'' and ''B'' (which might contain some variables) produce the same value for all values of the variables within a certain range of validity. In other words, ''A'' = ''B'' is an identity if ''A'' and ''B'' define the same functions, and an identity is an equality between functions that are differently defined. For example, (a+b)^2 = a^2 + 2ab + b^2 and \cos^2\theta + \sin^2\theta =1 are identities. Identities are sometimes indicated by the triple bar symbol instead of , the equals sign. Common identities Algebraic identities Certain identities, such as a+0=a and a+(-a)=0, form the basis of algebra, while other identities, such as (a+b)^2 = a^2 + 2ab +b^2 and a^2 - b^2 = (a+b)(a-b), can be useful in simplifying algebraic expressions and expanding them. Trigonometric identities Geometrically, trigonometric ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inheritance (computer Science)
In object-oriented programming, inheritance is the mechanism of basing an object or class upon another object ( prototype-based inheritance) or class ( class-based inheritance), retaining similar implementation. Also defined as deriving new classes ( sub classes) from existing ones such as super class or base class and then forming them into a hierarchy of classes. In most class-based object-oriented languages, an object created through inheritance, a "child object", acquires all the properties and behaviors of the "parent object" , with the exception of: constructors, destructor, overloaded operators and friend functions of the base class. Inheritance allows programmers to create classes that are built upon existing classes, to specify a new implementation while maintaining the same behaviors ( realizing an interface), to reuse code and to independently extend original software via public classes and interfaces. The relationships of objects or classes through inheritance give ris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |