|
Coclass Conjectures
In mathematics, the coclass of a finite ''p''-group of order ''p''''n'' is ''n'' − ''c'', where ''c'' is the class. The coclass conjectures The coclass conjectures were introduced by and proved by and . They are: *Conjecture A: Every ''p''-group has a normal subgroup of class 2 with index depending only on ''p'' and its coclass. *Conjecture B: The solvable length of a ''p''-group can be bounded in terms of ''p'' and the coclass. *Conjecture C: A pro ''p''-group of finite coclass is solvable. *Conjecture D: There are only finitely many pro ''p''-groups of given coclass. *Conjecture E: There are only finitely many solvable pro ''p''-groups of given coclass. See also *Descendant tree (group theory) In mathematics, specifically group theory, a descendant tree is a hierarchical structure that visualizes parent-descendant relations between isomorphism classes of finite groups of prime power order p^n, for a fixed prime number p and varying intege ... References ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-group
In mathematics, specifically group theory, given a prime number ''p'', a ''p''-group is a group in which the order of every element is a power of ''p''. That is, for each element ''g'' of a ''p''-group ''G'', there exists a nonnegative integer ''n'' such that the product of ''pn'' copies of ''g'', and not fewer, is equal to the identity element. The orders of different elements may be different powers of ''p''. Abelian ''p''-groups are also called ''p''-primary or simply primary. A finite group is a ''p''-group if and only if its order (the number of its elements) is a power of ''p''. Given a finite group ''G'', the Sylow theorems guarantee the existence of a subgroup of ''G'' of order ''pn'' for every prime power ''pn'' that divides the order of ''G''. Every finite ''p''-group is nilpotent. The remainder of this article deals with finite ''p''-groups. For an example of an infinite abelian ''p''-group, see Prüfer group, and for an example of an infinite simple ''p''-grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis (still a conjecture) or Fermat's Last Theorem (a conjecture until proven in 1995 by Andrew Wiles), have shaped much of mathematical history as new areas of mathematics are developed in order to prove them. Important examples Fermat's Last Theorem In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, ''b'', and ''c'' can satisfy the equation ''a^n + b^n = c^n'' for any integer value of ''n'' greater than two. This theorem was first conjectured by Pierre de Fermat in 1637 in the margin of a copy of '' Arithmetica'', where he claimed that he had a proof that was too large to fit in the margin. The first successful proof was released in 1994 by Andrew Wiles, and formally published in 1995, after 358 years of effort by mathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-group
In mathematics, specifically group theory, given a prime number ''p'', a ''p''-group is a group in which the order of every element is a power of ''p''. That is, for each element ''g'' of a ''p''-group ''G'', there exists a nonnegative integer ''n'' such that the product of ''pn'' copies of ''g'', and not fewer, is equal to the identity element. The orders of different elements may be different powers of ''p''. Abelian ''p''-groups are also called ''p''-primary or simply primary. A finite group is a ''p''-group if and only if its order (the number of its elements) is a power of ''p''. Given a finite group ''G'', the Sylow theorems guarantee the existence of a subgroup of ''G'' of order ''pn'' for every prime power ''pn'' that divides the order of ''G''. Every finite ''p''-group is nilpotent. The remainder of this article deals with finite ''p''-groups. For an example of an infinite abelian ''p''-group, see Prüfer group, and for an example of an infinite simple ''p''-grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgroup
In group theory, a branch of mathematics, given a group ''G'' under a binary operation ∗, a subset ''H'' of ''G'' is called a subgroup of ''G'' if ''H'' also forms a group under the operation ∗. More precisely, ''H'' is a subgroup of ''G'' if the restriction of ∗ to is a group operation on ''H''. This is often denoted , read as "''H'' is a subgroup of ''G''". The trivial subgroup of any group is the subgroup consisting of just the identity element. A proper subgroup of a group ''G'' is a subgroup ''H'' which is a proper subset of ''G'' (that is, ). This is often represented notationally by , read as "''H'' is a proper subgroup of ''G''". Some authors also exclude the trivial group from being proper (that is, ). If ''H'' is a subgroup of ''G'', then ''G'' is sometimes called an overgroup of ''H''. The same definitions apply more generally when ''G'' is an arbitrary semigroup, but this article will only deal with subgroups of groups. Subgroup tests Suppose th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
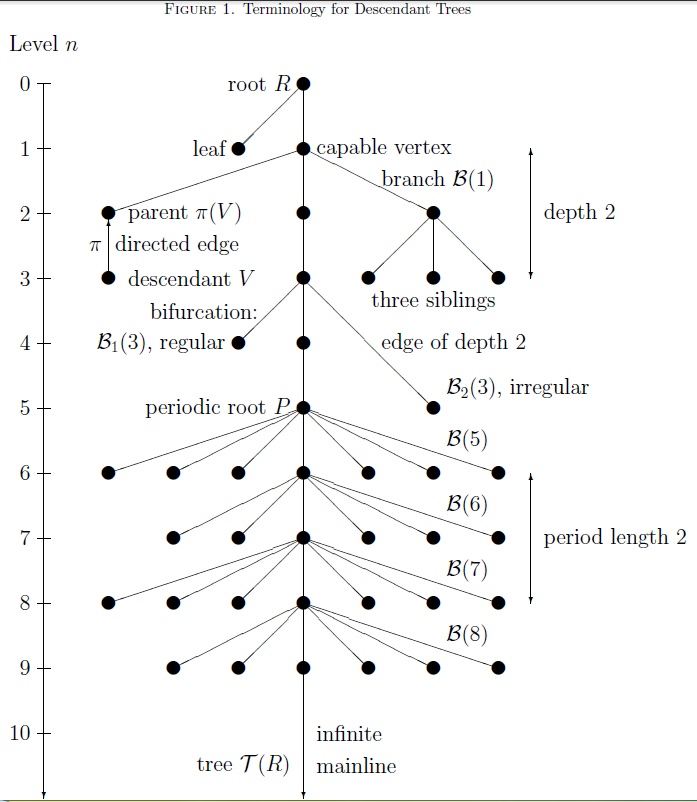
Descendant Tree (group Theory)
In mathematics, specifically group theory, a descendant tree is a hierarchical structure that visualizes parent-descendant relations between isomorphism classes of finite groups of prime power order p^n, for a fixed prime number p and varying integer exponents n\ge 0. Such groups are briefly called ''finite'' ''p-groups''. The ''vertices'' of a descendant tree are isomorphism classes of finite ''p''-groups. Additionally to their ''order'' p^n, finite ''p''-groups have two further related invariants, the ''nilpotency class'' c and the coclass r=n-c. It turned out that descendant trees of a particular kind, the so-called pruned coclass trees whose infinitely many vertices share a common coclass r, reveal a repeating finite pattern. These two crucial properties of finiteness and periodicity admit a characterization of all members of the tree by finitely many parametrized presentations. Consequently, descendant trees play a fundamental role in the classification of finite ''p''-gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |