|
Cephalometric Analysis
Cephalometric analysis is the clinical application of cephalometry. It is analysis of the dental and skeletal relationships of a human skull. It is frequently used by dentists, orthodontists, and oral and maxillofacial surgeons as a treatment planning tool. Two of the more popular methods of analysis used in orthodontology are the Steiner analysis (named after Cecil C. Steiner) and the Downs analysis (named after William B. Downs). There are other methods as well which are listed below. Cephalometric radiographs Cephalometric analysis depends on cephalometric radiography to study relationships between bony and soft tissue landmarks and can be used to diagnose facial growth abnormalities prior to treatment, in the middle of treatment to evaluate progress, or at the conclusion of treatment to ascertain that the goals of treatment have been met. A Cephalometric radiograph is a radiograph of the head taken in a Cephalometer (Cephalostat) that is a head-holding device introduced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clinical Medicine
Medicine is the science and practice of caring for a patient, managing the diagnosis, prognosis, prevention, treatment, palliation of their injury or disease, and promoting their health. Medicine encompasses a variety of health care practices evolved to maintain and restore health by the prevention and treatment of illness. Contemporary medicine applies biomedical sciences, biomedical research, genetics, and medical technology to diagnose, treat, and prevent injury and disease, typically through pharmaceuticals or surgery, but also through therapies as diverse as psychotherapy, external splints and traction, medical devices, biologics, and ionizing radiation, amongst others. Medicine has been practiced since prehistoric times, and for most of this time it was an art (an area of skill and knowledge), frequently having connections to the religious and philosophical beliefs of local culture. For example, a medicine man would apply herbs and say prayers for healing, or an ancie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
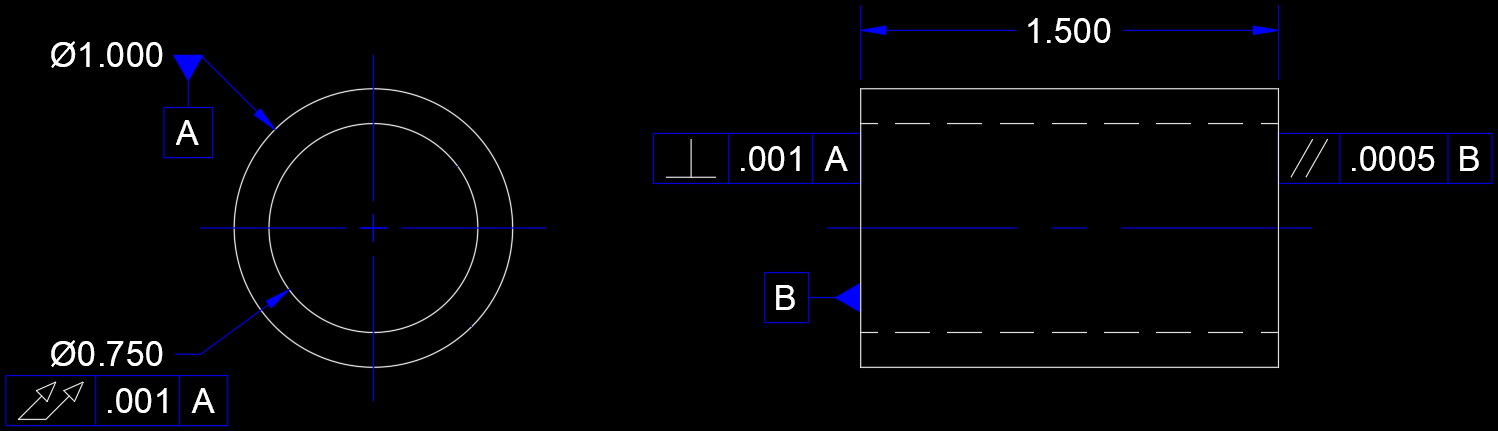
Datum Reference
A datum reference or just datum (plural: datumsThe plural of this word sense, sense of the word ''wikt:datum#Noun, datum'' is ''datums'' by convention, in contrast with the other senses of the word in which ''data'' usually serves as both the plural form and the mass noun counterpart.) ) is some important part of an object—such as a point (geometry), point, line (geometry), line, plane (geometry), plane, hole, set of holes, or pair of surface (mathematics), surfaces—that serves as a reference in defining the geometry of the object and (often) in measuring aspects of the actual geometry to assess how closely they match with the real versus nominal value, nominal value, which may be an ideal, standard, average, or desired value. For example, on a car's wheel, the lug nut holes define a wikt:bolt circle#Noun, bolt circle that is a datum from which the location of the rim can be defined and measured. This matters because the hub and rim need to be concentric objects, concentric to w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basion
The foramen magnum ( la, great hole) is a large, oval-shaped opening in the occipital bone of the skull. It is one of the several oval or circular openings (foramina) in the base of the skull. The spinal cord, an extension of the medulla oblongata, passes through the foramen magnum as it exits the cranial cavity. Apart from the transmission of the medulla oblongata and its membranes, the foramen magnum transmits the vertebral arteries, the anterior and posterior spinal arteries, the tectorial membranes and alar ligaments. It also transmits the accessory nerve into the skull. The foramen magnum is a very important feature in bipedal mammals. One of the attributes of a biped's foramen magnum is a forward shift of the anterior border of the cerebellar tentorium; this is caused by the shortening of the cranial base. Studies on the foramen magnum position have shown a connection to the functional influences of both posture and locomotion. The forward shift of the foramen magnum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mandibular Symphysis
In human anatomy, the facial skeleton of the skull the external surface of the mandible is marked in the median line by a faint ridge, indicating the mandibular symphysis (Latin: ''symphysis menti'') or line of junction where the two lateral halves of the mandible typically fuse at an early period of life (1-2 years). It is not a true symphysis as there is no cartilage between the two sides of the mandible. This ridge divides below and encloses a triangular eminence, the mental protuberance, the base of which is depressed in the center but raised on either side to form the mental tubercle. The lowest (most inferior) end of the mandibular symphysis — the point of the chin — is called the "menton". It serves as the origin for the geniohyoid and the genioglossus muscles. Other animals Solitary mammalian carnivores that rely on a powerful canine bite to subdue their prey have a strong mandibular symphysis, while pack hunters delivering shallow bites have a weaker one. When filter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
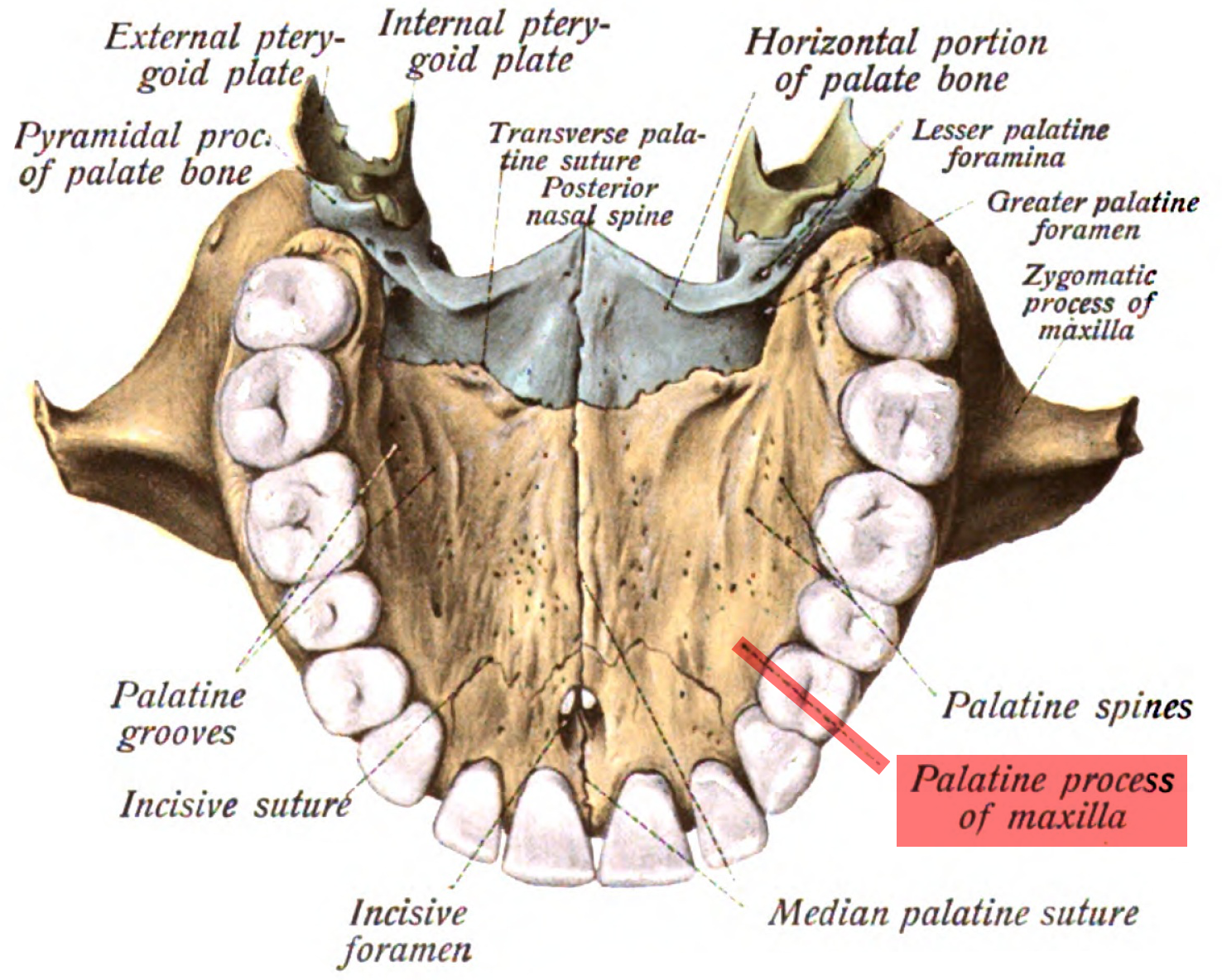
Maxilla
The maxilla (plural: ''maxillae'' ) in vertebrates is the upper fixed (not fixed in Neopterygii) bone of the jaw formed from the fusion of two maxillary bones. In humans, the upper jaw includes the hard palate in the front of the mouth. The two maxillary bones are fused at the intermaxillary suture, forming the anterior nasal spine. This is similar to the mandible (lower jaw), which is also a fusion of two mandibular bones at the mandibular symphysis. The mandible is the movable part of the jaw. Structure In humans, the maxilla consists of: * The body of the maxilla * Four processes ** the zygomatic process ** the frontal process of maxilla ** the alveolar process ** the palatine process * three surfaces – anterior, posterior, medial * the Infraorbital foramen * the maxillary sinus * the incisive foramen Articulations Each maxilla articulates with nine bones: * two of the cranium: the frontal and ethmoid * seven of the face: the nasal, zygomatic, lacrimal, inferior n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nasion
The nasion () is the most anterior point of the frontonasal suture that joins the nasal part of the frontal bone and the nasal bones. It marks the midpoint at the intersection of the frontonasal suture with the internasal suture joining the nasal bones. It is visible on the face as a distinctly depressed area directly between the eyes, just superior to the bridge of the nose. It is a cephalometric landmark that is just below the glabella The glabella, in humans, is the area of skin between the eyebrows and above the nose. The term also refers to the underlying bone that is slightly depressed, and joins the two brow ridges. It is a cephalometric landmark that is just superior to .... References {{Authority control Facial features ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sella Turcica
The sella turcica (Latin for 'Turkish saddle') is a saddle-shaped depression in the body of the sphenoid bone of the human skull and of the skulls of other hominids including chimpanzees, gorillas and orangutans. It serves as a cephalometric landmark. The pituitary gland or hypophysis is located within the most inferior aspect of the sella turcica, the hypophyseal fossa. Structure The sella turcica is located in the sphenoid bone behind the chiasmatic groove and the tuberculum sellae. It belongs to the middle cranial fossa. The sella turcica's most inferior portion is known as the hypophyseal fossa (the "seat of the saddle"), and contains the pituitary gland (hypophysis). In front of the hypophyseal fossa is the tuberculum sellae. Completing the formation of the saddle posteriorly is the dorsum sellae, which is continuous with the clivus, inferoposteriorly. The dorsum sellae is terminated laterally by the posterior clinoid processes. Development It is widely believed that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (mathematics)
In mathematics, a projection is a mapping of a set (or other mathematical structure) into a subset (or sub-structure), which is equal to its square for mapping composition, i.e., which is idempotent. The restriction to a subspace of a projection is also called a ''projection'', even if the idempotence property is lost. An everyday example of a projection is the casting of shadows onto a plane (sheet of paper): the projection of a point is its shadow on the sheet of paper, and the projection (shadow) of a point on the sheet of paper is that point itself (idempotency). The shadow of a three-dimensional sphere is a closed disk. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the three-dimensional Euclidean space onto a plane in it, like the shadow example. The two main projections of this kind are: * The projection from a point onto a plane or central projection: If ''C'' is a point, called the center of projection, then the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane (geometry)
In mathematics, a plane is a Euclidean (flat), two-dimensional surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with one of a room's walls, infinitely extended, or they may enjoy an independent existence in their own right, as in the setting of two-dimensional Euclidean geometry. Sometimes the word ''plane'' is used more generally to describe a two-dimensional surface, for example the hyperbolic plane and elliptic plane. When working exclusively in two-dimensional Euclidean space, the definite article is used, so ''the'' plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, often in the plane. Euclidean geometry Euclid set forth the first great landmark of mathematical thought, an axiomatic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. Angles formed by two rays lie in the plane (geometry), plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection. ''Angle'' is also used to designate the measurement, measure of an angle or of a Rotation (mathematics), rotation. This measure is the ratio of the length of a arc (geometry), circular arc to its radius. In the case of a geometric angle, the arc is centered at the vertex and delimited by the sides. In the case of a rotation, the arc is centered at the center of the rotation and delimited by any other point and its image by the rotation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a '' directed line segment'', or graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \overrightarrow . A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word ''vector'' means "carrier". It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operations whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axis (mathematics)
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |