|
Call Option
In finance, a call option, often simply labeled a "call", is a contract between the buyer and the seller of the call Option (finance), option to exchange a Security (finance), security at a set price. The buyer of the call option has the right, but not the obligation, to buy an agreed quantity of a particular commodity or financial instrument (the underlying) from the seller of the option at or before a certain time (the Expiration (options), expiration date) for a certain price (the strike price). This effectively gives the buyer a Long (finance), ''long'' position in the given asset. The seller (or "writer") is obliged to sell the commodity or financial instrument to the buyer if the buyer so decides. This effectively gives the seller a Short (finance), ''short'' position in the given asset. The buyer pays a fee (called a Insurance, premium) for this right. The term "call" comes from the fact that the owner has the right to "call the stock away" from the seller. Price of opt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Long Call Option
Long may refer to: Measurement * Long, characteristic of something of great time, duration * Long, characteristic of something of great length * Longitude (abbreviation: long.), a geographic coordinate * Longa (music), note value in early music mensural notation Places Asia * Long District, Laos * Long District, Phrae, Thailand * Longjiang (other) or River Long (lit. "dragon river"), one of several rivers in China * Yangtze River or Changjiang (lit. "Long River"), China Elsewhere * Long, Somme, France People * Long (Chinese surname) * Long (Western surname) Fictional characters * Long (Bloody Roar), Long (''Bloody Roar''), in the video game series * Long, Aeon of Permanence in Honkai: Star Rail Sports * Long, a Fielding (cricket)#Modifiers, fielding term in cricket * Long, in tennis and similar games, beyond the service line during a serve and beyond the baseline during play Other uses * , a U.S. Navy ship name * Long (finance), a position in finance, especially sto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
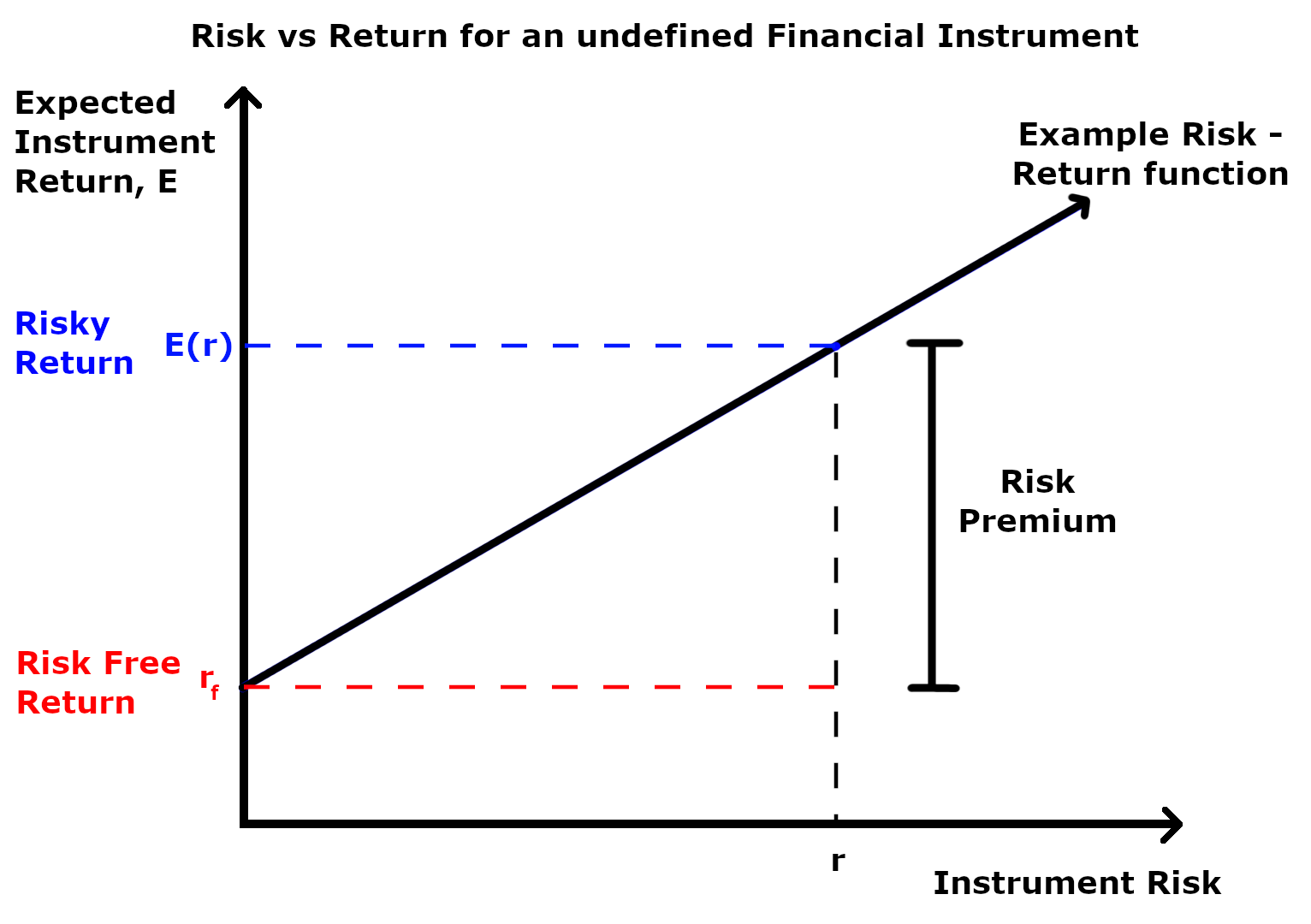
Risk Premium
A risk premium is a measure of excess return that is required by an individual to compensate being subjected to an increased level of risk. It is used widely in finance and economics, the general definition being the expected risky Rate of return, return less the Risk-free interest rate, risk-free return, as demonstrated by the formula below. Risk \ premium = E(r) - r_f Where E(r) is the risky expected rate of return and r_f is the risk-free return. The inputs for each of these variables and the ultimate interpretation of the risk premium value differs depending on the application as explained in the following sections. Regardless of the application, the market premium can be volatile as both comprising variables can be impacted independent of each other by both cyclical and abrupt changes. This means that the market premium is dynamic in nature and ever-changing. Additionally, a general observation regardless of application is that the risk premium is larger during economic do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Put–call Parity
In financial mathematics, the put–call parity defines a relationship between the price of a European call option and European put option, both with the identical strike price and expiry, namely that a portfolio of a long call option and a short put option is equivalent to (and hence has the same value as) a single forward contract at this strike price and expiry. This is because if the price at expiry is above the strike price, the call will be exercised, while if it is below, the put will be exercised, and thus in either case one unit of the asset will be purchased for the strike price, exactly as in a forward contract. The validity of this relationship requires that certain assumptions be satisfied; these are specified and the relationship is derived below. In practice transaction costs and financing costs (leverage) mean this relationship will not exactly hold, but in liquid markets the relationship is close to exact. Assumptions Put–call parity is a static replication, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Put Option
In finance, a put or put option is a derivative instrument in financial markets that gives the holder (i.e. the purchaser of the put option) the right to sell an asset (the ''underlying''), at a specified price (the ''strike''), by (or on) a specified date (the '' expiry'' or ''maturity'') to the ''writer'' (i.e. seller) of the put. The purchase of a put option is interpreted as a negative sentiment about the future value of the underlying stock. page 15 , 4.2.3 Positive and negative sentiment The term "put" comes from the fact that the owner has the right to "put up for sale" the stock or index. Puts may also be combined with other derivatives as part of more complex investment strategies, and in particular, may be useful for hedging. Holding a European put option is equivalent to holding the corresponding call option and selling an appropriate forward contract. This equivalence is called " put-call parity". Put options are most commonly used in the stock market to prot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pre-emption Right
A pre-emption right, right of pre-emption, or first option to buy is a contractual right to acquire certain property newly coming into existence before it can be offered to any other person or entity. It comes from the Latin verb ''emo, emere, emi, emptum'', to buy or purchase, plus the inseparable preposition ''pre'', before. A right to acquire existing property in preference to any other person is usually referred to as a ''right of first refusal''. Company shares In practice, the most common form of pre-emption right is the right of existing shareholders to acquire new shares issued by a company in a rights issue, usually a public offering. In this context, the pre-emptive right is also called subscription right or subscription privilege. It is the right but not the obligation of existing shareholders to buy the new shares before they are offered to the public. In that way, existing shareholders can maintain their proportional ownership of the company and thus prevent stock dil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Option Time Value
In finance, the time value (TV) (''extrinsic'' or ''instrumental'' value) of an option (finance), option is the premium a rational investor would pay over its ''current'' exercise value (intrinsic value (finance), intrinsic value), based on the probability it will increase in value before expiry. For an Option style, American option this value is always greater than zero in a fair market, thus an option is ''always'' worth more than its current exercise value. As an option can be thought of as 'price insurance' (e.g., an airline insuring against unexpected soaring fuel costs caused by a hurricane), TV can be thought of as the ''risk premium'' the option seller charges the buyer—the higher the expected risk (volatility \cdot time), the higher the premium. Conversely, TV can be thought of as the price an investor is willing to pay for potential upside. Time value decays to zero at expiration, with a general rule that it will lose of its value during the first half of its life and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Naked Put
A naked option or uncovered option is an options strategy where the options contract writer (i.e., the seller) does not hold the underlying asset to cover the contract in case of assignment (like in a covered option). Nor does the seller hold any option of the same class on the same underlying asset that could protect against potential losses (like in an options spread). A naked option involving a "call" is called a "naked call" or "uncovered call", while one involving a " put" is a "naked put" or "uncovered put". The naked option is one of riskiest options strategies, and therefore most brokers restrict them to only those traders that have the highest options level approval and have a margin account. Naked options are attractive because the seller receives the premium cost of the option without buying a corresponding position to hedge against potential losses. In the case of a naked put, the seller hopes that the underlying equity or stock price stays the same or rises. In the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Moneyness
In finance, moneyness is the relative position of the current price (or future price) of an underlying asset (e.g., a stock) with respect to the strike price of a derivative, most commonly a call option or a put option. Moneyness is firstly a three-fold classification: * If the derivative would have positive intrinsic value if it were to expire today, it is said to be in the money (ITM); * If the derivative would be worthless if expiring with the underlying at its current price, it is said to be out of the money (OTM); * And if the current underlying price and strike price are equal, the derivative is said to be at the money (ATM). There are two slightly different definitions, according to whether one uses the current price (spot) or future price (forward), specified as "at the money spot" or "at the money forward", etc. This rough classification can be quantified by various definitions to express the moneyness as a number, measuring how far the asset is in the money or out o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Covered Call
A covered option is a financial transaction in which the holder of securities sells (or "writes") a type of financial options contract known as a "call" or a " put" against stock that they own or are shorting. The seller of a covered option receives compensation, or "premium", for this transaction, which can limit losses; however, the act of selling a covered option also limits their profit potential to the upside. One covered option is sold for every hundred shares the seller wishes to cover. A covered option constructed with a call is called a "covered call", while one constructed with a put is a "covered put". This strategy is generally considered conservative because the seller of a covered option reduces both their risk and their return. Characteristics Covered calls are bullish by nature, while covered puts are bearish. The payoff from selling a covered call is identical to selling a short naked put. Both variants are a short implied volatility strategy. Covered call ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Black–Scholes Model
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing Derivative (finance), derivative investment instruments. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of option style, European-style option (finance), options and shows that the option has a ''unique'' price given the risk of the security and its expected return (instead replacing the security's expected return with the risk-neutral rate). The equation and model are named after economists Fischer Black and Myron Scholes. Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited. The main principle behind the model is to hedge (finance), hedge the option by buying and selling the underlying asset in a specific way to eliminate risk. This type of hedging is called "continuou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Financial Mathematics
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the Finance#Quantitative_finance, financial field. In general, there exist two separate branches of finance that require advanced quantitative techniques: Derivative (finance), derivatives pricing on the one hand, and risk management, risk and Investment management#Investment managers and portfolio structures, portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often with the help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when investment ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |