|
Compatibility (mechanics)
In continuum mechanics, a compatible deformation (or strain) tensor field in a body is that ''unique'' tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.C Amrouche, PG Ciarlet, L Gratie, S Kesavan, On Saint Venant's compatibility conditions and Poincaré's lemma, C. R. Acad. Sci. Paris, Ser. I, 342 (2006), 887-891. In the continuum description of a solid body we imagine the body to be composed of a set of infinitesimal volumes or material points. Each volume is assumed to be connected to its neighbors without any gaps or overlaps. Certain mathematical conditions have to be satisfied to ensure that gaps/overlaps do n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Mechanics
Continuum mechanics is a branch of mechanics that deals with the deformation of and transmission of forces through materials modeled as a ''continuous medium'' (also called a ''continuum'') rather than as discrete particles. Continuum mechanics deals with ''deformable bodies'', as opposed to rigid bodies. A continuum model assumes that the substance of the object completely fills the space it occupies. While ignoring the fact that matter is made of atoms, this provides a sufficiently accurate description of matter on length scales much greater than that of inter-atomic distances. The concept of a continuous medium allows for intuitive analysis of bulk matter by using differential equations that describe the behavior of such matter according to physical laws, such as mass conservation, momentum conservation, and energy conservation. Information about the specific material is expressed in constitutive relationships. Continuum mechanics treats the physical properties of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Strain
Plane most often refers to: * Aero- or airplane, a powered, fixed-wing aircraft * Plane (geometry), a flat, 2-dimensional surface * Plane (mathematics), generalizations of a geometrical plane Plane or planes may also refer to: Biology * Plane (tree) or ''Platanus'', wetland native plant * ''Planes'' (genus), marsh crabs in Grapsidae * '' Bindahara phocides'', the plane butterfly of Asia Maritime transport * Planing (boat), where weight is predominantly supported by hydrodynamic lift * ''Plane'' (wherry), a Norfolk canal boat, in use 1931–1949 Music *"Planes", a 1976 song by Colin Blunstone *"Planes (Experimental Aircraft)", a 1989 song by Jefferson Airplane from '' Jefferson Airplane'' *" Planez", originally "Planes", a 2015 song by Jeremih *"The Plane", a 1987 song on the '' Empire of the Sun'' soundtrack *"The Plane", a 1997 song by Kinito Méndez Other entertainment * Plane (''Dungeons & Dragons''), any fictional realm of the D&D roleplaying game's multiverse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Derivative (continuum Mechanics)
The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical simulations. The directional derivative provides a systematic way of finding these derivatives. Derivatives with respect to vectors and second-order tensors The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken. Derivatives of scalar valued functions of vectors Let ''f''(v) be a real valued function of the vector v. Then the derivative of ''f''(v) with respect to v (or at v) is the vector defined through its dot product with any vector u being \frac\cdot\mathbf = Df(\mathbf) mathbf= \left frac~f(\mathbf + \alpha~\mathbf)\right for all vectors u. The above dot product yields a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal Strain Theory
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller (indeed, infinitesimally smaller) than any relevant dimension of the body; so that its geometry and the constitutive properties of the material (such as density and stiffness) at each point of space can be assumed to be unchanged by the deformation. With this assumption, the equations of continuum mechanics are considerably simplified. This approach may also be called small deformation theory, small displacement theory, or small displacement-gradient theory. It is contrasted with the finite strain theory where the opposite assumption is made. The infinitesimal strain theory is commonly adopted in civil and mechanical engineering for the stress analysis of structures built from relatively stiff elastic materials like concrete and steel, since a common goal in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
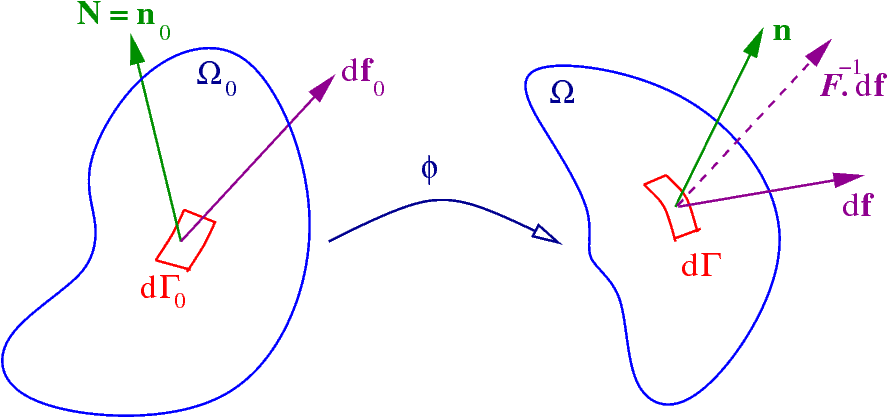
Deformation (mechanics)
In physics and continuum mechanics, deformation is the change in the shape (geometry), shape or size of an object. It has dimension (physics), dimension of length with SI unit of metre (m). It is quantified as the residual displacement (geometry), displacement of particles in a non-rigid body, from an configuration to a configuration, excluding the body's average translation (physics), translation and rotation (its rigid transformation). A ''configuration'' is a set containing the position (geometry), positions of all particles of the body. A deformation can occur because of structural load, external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. In a continuous body, a ''deformation field'' results from a Stress (physics), stress field due to applied forces or because of some changes in the conditions of the body. The relation between stre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Elasticity
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics. The fundamental assumptions of linear elasticity are infinitesimal strains — meaning, "small" deformations — and linear relationships between the components of stress and strain — hence the "linear" in its name. Linear elasticity is valid only for stress states that do not produce yielding. Its assumptions are reasonable for many engineering materials and engineering design scenarios. Linear elasticity is therefore used extensively in structural analysis and engineering design, often with the aid of finite element analysis. Mathematical formulation Equations governing a linear elastic boundary value problem are based on three tensor partial differential equations for the balance of linear momentum and six in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes' Theorem
Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls, or simply the curl theorem, is a theorem in vector calculus on \R^3. Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical theorem of Stokes can be stated in one sentence: : The line integral of a vector field over a loop is equal to the surface integral of its '' curl'' over the enclosed surface. Stokes' theorem is a special case of the generalized Stokes theorem. In particular, a vector field on \R^3 can be considered as a 1-form in which case its curl is its exterior derivative, a 2-form. Theorem Let \Sigma be a smooth oriented surface in \R^3 with boundary \partial \Sigma \equiv \Gamma . If a vector field \mathbf(x,y,z) = (F_x(x, y, z), F_y(x, y, z), F_z(x, y, z)) is defined and has continuous first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compatibility Mechanics
Compatibility may refer to: Computing * Backward compatibility, in which newer systems can understand data generated by older ones * Compatibility card, an expansion card for hardware emulation of another device * Compatibility layer, components that allow for non-native support of components ** Compatibility mode, software mechanism in which a software emulates an older version of software * Computer compatibility, of a line of machines ** IBM PC compatible, computers that are generally similar to the original IBM PC, XT, or AT * Forward compatibility, in which older systems can understand data generated by newer ones * Hardware compatibility, between different pieces of computer hardware * License compatibility, of software licenses * Pin compatibility, in devices that have the same functions assigned to the same particular pins * Software compatibility, between different pieces of software ** Software incompatibility Science and mathematics * Biocompatibility, a description ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Derivative (continuum Mechanics)
The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical simulations. The directional derivative provides a systematic way of finding these derivatives. Derivatives with respect to vectors and second-order tensors The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken. Derivatives of scalar valued functions of vectors Let ''f''(v) be a real valued function of the vector v. Then the derivative of ''f''(v) with respect to v (or at v) is the vector defined through its dot product with any vector u being \frac\cdot\mathbf = Df(\mathbf) mathbf= \left frac~f(\mathbf + \alpha~\mathbf)\right for all vectors u. The above dot product yields a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Displacement Of A Continuum
Displacement may refer to: Physical sciences Mathematics and physics *Displacement (geometry), is the difference between the final and initial position of a point trajectory (for instance, the center of mass of a moving object). The actual path covered to reach the final position is irrelevant. **Particle displacement, a measurement of distance of the movement of a particle in a medium as it transmits a wave (represented in mathematics by the lower-case Greek letter ξ) **Displacement field (mechanics), an assignment of displacement vectors for all points in a body that is displaced from one state to another **Electric displacement field, as appears in Maxwell's equations *Wien's displacement law, a relation concerning the spectral distribution of blackbody radiation *Angular displacement, a change in orientation of a rigid body, the amount of rotation about a fixed axis. Engineering *Engine displacement, the total volume of air/fuel mixture an engine can draw in during one compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvilinear Coordinates
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is invertible, locally invertible (a one-to-one map) at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name ''curvilinear coordinates'', coined by the French mathematician Gabriel Lamé, Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved. Well-known examples of curvilinear coordinate systems in three-dimensional Euclidean space (R3) are Cylindrical coordinate system, cylindrical and spherical coordinates, spherical coordinates. A Cartesian coordinate surface in this space is a coordinate plane; for example ''z'' = 0 defines the ''x''-''y'' plane. In the same space, the coordinate surface ''r'' = 1 in spherical coordinates i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |