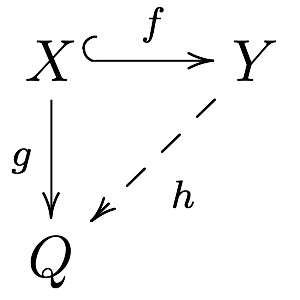|
Category Of Metric Spaces
In category theory, Met is a category that has metric spaces as its objects and metric maps ( continuous functions between metric spaces that do not increase any pairwise distance) as its morphisms. This is a category because the composition of two metric maps is again a metric map. It was first considered by . Arrows The monomorphisms in Met are the injective metric maps. The epimorphisms are the metric maps for which the domain of the map has a dense image in the range. The isomorphisms are the isometries, i.e. metric maps which are injective, surjective, and distance-preserving. As an example, the inclusion of the rational numbers into the real numbers is a monomorphism and an epimorphism, but it is clearly not an isomorphism; this example shows that Met is not a balanced category. Objects The empty metric space is the initial object of Met; any singleton metric space is a terminal object. Because the initial object and the terminal objects differ, there are no zero objec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in most areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient space (other), quotient spaces, direct products, completion, and duality (mathematics), duality. Many areas of computer science also rely on category theory, such as functional programming and Semantics (computer science), semantics. A category (mathematics), category is formed by two sorts of mathematical object, objects: the object (category theory), objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. Metapho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' meaning "equal", and μέτρον ''metron'' meaning "measure". If the transformation is from a metric space to itself, it is a kind of geometric transformation known as a motion. Introduction Given a metric space (loosely, a set and a scheme for assigning distances between elements of the set), an isometry is a transformation which maps elements to the same or another metric space such that the distance between the image elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional Euclidean space, two geometric figures are congruent if they are related by an isometry; the isometry that relates them is either a rigid motion (translation or rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group (mathematics), group that is a subgroup. When some object X is said to be embedded in another object Y, the embedding is given by some Injective function, injective and structure-preserving map f:X\rightarrow Y. The precise meaning of "structure-preserving" depends on the kind of mathematical structure of which X and Y are instances. In the terminology of category theory, a structure-preserving map is called a morphism. The fact that a map f:X\rightarrow Y is an embedding is often indicated by the use of a "hooked arrow" (); thus: f : X \hookrightarrow Y. (On the other hand, this notation is sometimes reserved for inclusion maps.) Given X and Y, several different embeddings of X in Y may be possible. In many cases of interest there is a standard (or "canonical") embedding, like those of the natural numbers in the integers, the integers i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helly Family
In combinatorics, a Helly family of order is a family of Set (mathematics), sets in which every minimal ''subfamily with an empty Intersection (set theory), intersection'' has or fewer sets in it. Equivalently, every finite subfamily such that every -fold intersection is non-empty has non-empty total intersection.. The -Helly property is the property of being a Helly family of order .. See in particular Section 2.5, "Helly Property"pp. 393–394 The number is frequently omitted from these names in the case that . Thus, a set-family has the Helly property if, for every sets s_1,\ldots,s_n in the family, if \forall i,j\in[n]: s_i \cap s_j \neq\emptyset , then s_1 \cap \cdots \cap s_n \neq\emptyset . These concepts are named after Eduard Helly (1884–1943); Helly's theorem on convex sets, which gave rise to this notion, states that convex sets in Euclidean space of dimension are a Helly family of order . Examples * In the family of all subsets of the set , the subfamil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Metric Space
In metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher- dimensional vector spaces. These properties can be defined in two seemingly different ways: hyperconvexity involves the intersection properties of closed balls in the space, while injectivity involves the isometric embeddings of the space into larger spaces. However it is a theorem of that these two different types of definitions are equivalent. Hyperconvexity A metric space X is said to be hyperconvex if it is convex and its closed balls have the binary Helly property. That is: #Any two points x and y can be connected by the isometric image of a line segment of length equal to the distance between the points (i.e. X is a path space). #If F is any family of closed balls _r(p) = \ such that each pair of balls in F meets, then there exists a point x common to all the balls in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object. Definition An object Q in a category \mathbf is said to be injective if for every monomorphism f: X \to Y and every morphism g: X \to Q there exists a morphism h: Y \to Q extending g to Y, i.e. such that h \circ f = g. That is, every morphism X \to Q factors through every monomorphism X \hookrightarrow Y. The morphism h in the above definition is not required to be uniquely determined by f and g. In a locally small category, it is equivalent to require that the hom functor \operatorname_(-,Q) carries monomorphisms in \mathbf to surjective set maps. In Abelian categories The notion of injectivity was first formulated for abelian categories, and this is still one of its primary areas of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero Object
In category theory, a branch of mathematics, an initial object of a category is an object in such that for every object in , there exists precisely one morphism . The dual notion is that of a terminal object (also called terminal element): is terminal if for every object in there exists exactly one morphism . Initial objects are also called coterminal or universal, and terminal objects are also called final. If an object is both initial and terminal, it is called a zero object or null object. A pointed category is one with a zero object. A strict initial object is one for which every morphism into is an isomorphism. Examples * The empty set is the unique initial object in Set, the category of sets. Every one-element set ( singleton) is a terminal object in this category; there are no zero objects. Similarly, the empty space is the unique initial object in Top, the category of topological spaces and every one-point space is a terminal object in this category. * I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Terminal Object
In category theory, a branch of mathematics, an initial object of a category is an object in such that for every object in , there exists precisely one morphism . The dual notion is that of a terminal object (also called terminal element): is terminal if for every object in there exists exactly one morphism . Initial objects are also called coterminal or universal, and terminal objects are also called final. If an object is both initial and terminal, it is called a zero object or null object. A pointed category is one with a zero object. A strict initial object is one for which every morphism into is an isomorphism. Examples * The empty set is the unique initial object in Set, the category of sets. Every one-element set ( singleton) is a terminal object in this category; there are no zero objects. Similarly, the empty space is the unique initial object in Top, the category of topological spaces and every one-point space is a terminal object in this category. * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singleton (mathematics)
In mathematics, a singleton (also known as a unit set or one-point set) is a set with exactly one element. For example, the set \ is a singleton whose single element is 0. Properties Within the framework of Zermelo–Fraenkel set theory, the axiom of regularity guarantees that no set is an element of itself. This implies that a singleton is necessarily distinct from the element it contains, thus 1 and \ are not the same thing, and the empty set is distinct from the set containing only the empty set. A set such as \ is a singleton as it contains a single element (which itself is a set, but not a singleton). A set is a singleton if and only if its cardinality is . In von Neumann's set-theoretic construction of the natural numbers, the number 1 is ''defined'' as the singleton \. In axiomatic set theory, the existence of singletons is a consequence of the axiom of pairing: for any set ''A'', the axiom applied to ''A'' and ''A'' asserts the existence of \, which is the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Initial Object
In category theory, a branch of mathematics, an initial object of a category is an object in such that for every object in , there exists precisely one morphism . The dual notion is that of a terminal object (also called terminal element): is terminal if for every object in there exists exactly one morphism . Initial objects are also called coterminal or universal, and terminal objects are also called final. If an object is both initial and terminal, it is called a zero object or null object. A pointed category is one with a zero object. A strict initial object is one for which every morphism into is an isomorphism. Examples * The empty set is the unique initial object in Set, the category of sets. Every one-element set ( singleton) is a terminal object in this category; there are no zero objects. Similarly, the empty space is the unique initial object in Top, the category of topological spaces and every one-point space is a terminal object in this category. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empty Set
In mathematics, the empty set or void set is the unique Set (mathematics), set having no Element (mathematics), elements; its size or cardinality (count of elements in a set) is 0, zero. Some axiomatic set theories ensure that the empty set exists by including an axiom of empty set, while in other theories, its existence can be deduced. Many possible properties of sets are vacuously true for the empty set. Any set other than the empty set is called ''non-empty''. In some textbooks and popularizations, the empty set is referred to as the "null set". However, null set is a distinct notion within the context of measure theory, in which it describes a set of measure zero (which is not necessarily empty). Notation Common notations for the empty set include "", "\emptyset", and "∅". The latter two symbols were introduced by the Bourbaki group (specifically André Weil) in 1939, inspired by the letter Ø () in the Danish orthography, Danish and Norwegian orthography, Norwegian a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Balanced Category
In mathematics, especially in category theory, a balanced category is a category in which every bimorphism (a morphism that is both a monomorphism and epimorphism) is an isomorphism. The category of topological spaces is not balanced (since continuous bijections are not necessarily homeomorphisms), while a topos is balanced. This is one of the reasons why a topos is said to be nicer. Examples The following categories are balanced: *Set, the category of sets. *Grp, the category of groups. *An abelian category. *CHaus, the category of compact Hausdorff spaces (since a continuous bijection there is homeomorphic). An additive category In mathematics, specifically in category theory, an additive category is a preadditive category C admitting all finitary biproducts. Definition There are two equivalent definitions of an additive category: One as a category equipped wit ... may not be balanced. Contrary to what one might expect, a balanced pre-abelian category may not be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |