|
Beta (finance)
In finance, the beta (β or market beta or beta coefficient) is a measure of how an individual asset moves (on average) when the overall stock market increases or decreases. Thus, beta is a useful measure of the contribution of an individual asset to the risk of the market portfolio when it is added in small quantity. Thus, beta is referred to as an asset's non-diversifiable risk, its systematic risk, market risk, or hedge ratio. Beta is ''not'' a measure of idiosyncratic risk. Interpretation of values By definition, the value-weighted average of all market-betas of all investable assets with respect to the value-weighted market index is 1. If an asset has a beta above (below) 1, it indicates that its return moves more (less) than 1-to-1 with the return of the market-portfolio, on average. In practice, few stocks have negative betas (tending to go up when the market goes down). Most stocks have betas between 0 and 3. Treasury bills (like most fixed income instruments) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finance
Finance is the study and discipline of money, currency and capital assets. It is related to, but not synonymous with economics, the study of production, distribution, and consumption of money, assets, goods and services (the discipline of financial economics bridges the two). Finance activities take place in financial systems at various scopes, thus the field can be roughly divided into personal, corporate, and public finance. In a financial system, assets are bought, sold, or traded as financial instruments, such as currencies, loans, bonds, shares, stocks, options, futures, etc. Assets can also be banked, invested, and insured to maximize value and minimize loss. In practice, risks are always present in any financial action and entities. A broad range of subfields within finance exist due to its wide scope. Asset, money, risk and investment management aim to maximize value and minimize volatility. Financial analysis is viability, stability, and profitability asse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regression equation. The OLS estimator is consiste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Estimator
In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function (i.e., the posterior expected loss). Equivalently, it maximizes the posterior expectation of a utility function. An alternative way of formulating an estimator within Bayesian statistics is maximum a posteriori estimation. Definition Suppose an unknown parameter \theta is known to have a prior distribution \pi. Let \widehat = \widehat(x) be an estimator of \theta (based on some measurements ''x''), and let L(\theta,\widehat) be a loss function, such as squared error. The Bayes risk of \widehat is defined as E_\pi(L(\theta, \widehat)), where the expectation is taken over the probability distribution of \theta: this defines the risk function as a function of \widehat. An estimator \widehat is said to be a ''Bayes estimator'' if it minimizes the Bayes risk among all estimators. Equivalently, the estimator whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Toward The Mean
In statistics, regression toward the mean (also called reversion to the mean, and reversion to mediocrity) is the fact that if one sample of a random variable is extreme, the next sampling of the same random variable is likely to be closer to its mean. Furthermore, when many random variables are sampled and the most extreme results are intentionally picked out, it refers to the fact that (in many cases) a second sampling of these picked-out variables will result in "less extreme" results, closer to the initial mean of all of the variables. Mathematically, the strength of this "regression" effect is dependent on whether or not all of the random variables are drawn from the same distribution, or if there are genuine differences in the underlying distributions for each random variable. In the first case, the "regression" effect is statistically likely to occur, but in the second case, it may occur less strongly or not at all. Regression toward the mean is thus a useful concept to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Least Squares (mathematics)
Linear least squares (LLS) is the least squares approximation of linear functions to data. It is a set of formulations for solving statistical problems involved in linear regression, including variants for ordinary (unweighted), weighted, and generalized (correlated) residuals. Numerical methods for linear least squares include inverting the matrix of the normal equations and orthogonal decomposition methods. Main formulations The three main linear least squares formulations are: * Ordinary least squares (OLS) is the most common estimator. OLS estimates are commonly used to analyze both experimental and observational data. The OLS method minimizes the sum of squared residuals, and leads to a closed-form expression for the estimated value of the unknown parameter vector ''β'': \hat = (\mathbf^\mathsf\mathbf)^ \mathbf^\mathsf \mathbf, where \mathbf is a vector whose ''i''th element is the ''i''th observation of the dependent variable, and \mathbf is a matrix whose ''ij' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule (the estimator), the quantity of interest (the estimand) and its result (the estimate) are distinguished. For example, the sample mean is a commonly used estimator of the population mean. There are point and interval estimators. The point estimators yield single-valued results. This is in contrast to an interval estimator, where the result would be a range of plausible values. "Single value" does not necessarily mean "single number", but includes vector valued or function valued estimators. ''Estimation theory'' is concerned with the properties of estimators; that is, with defining properties that can be used to compare different estimators (different rules for creating estimates) for the same quantity, based on the same data. Such properties can be used to determine the best rules to use under given circumstances. However, in robust statistics, statistica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
United States Treasury Security
United States Treasury securities, also called Treasuries or Treasurys, are government debt instruments issued by the United States Department of the Treasury to finance government spending as an alternative to taxation. Since 2012, U.S. government debt has been managed by the Bureau of the Fiscal Service, succeeding the Bureau of the Public Debt. There are four types of marketable Treasury securities: Treasury bills, Treasury notes, Treasury bonds, and Treasury Inflation Protected Securities (TIPS). The government sells these securities in auctions conducted by the Federal Reserve Bank of New York, after which they can be traded in secondary markets. Non-marketable securities include savings bonds, issued to the public and transferable only as gifts; the State and Local Government Series (SLGS), purchaseable only with the proceeds of state and municipal bond sales; and the Government Account Series, purchased by units of the federal government. Treasury securities are b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MSCI EAFE
The MSCI EAFE Index is a stock market index that is designed to measure the equity market performance of developed markets outside of the U.S. & Canada. It is maintained by MSCI Inc., a provider of investment decision support tools; the EAFE acronym stands for Europe, Australasia and Far East. The index is market-capitalization weighted (meaning that the weight of securities is based on their respective market capitalizations). It first ranks each stock in the investable universe from largest to smallest by market capitalization. The largest 70% will compose the MSCI EAFE Large Cap (new index), the largest 85% will compose the MSCI EAFE Standard, and the largest 99% will compose the MSCI Investable Market index (IMI). The 71st to 85th percentiles represent the MSCI EAFE Mid Cap, and the 85th to 99th percentiles represent the MSCI EAFE Small Cap. The index includes a selection of stocks from 21 developed markets, but excludes those from the U.S. and Canada. The index has been ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asset Classes
In finance, an asset class is a group of financial instruments that have similar financial characteristics and behave similarly in the marketplace. We can often break these instruments into those having to do with real assets and those having to do with financial assets. Often, assets within the same asset class are subject to the same laws and regulations; however, this is not always true. For instance, futures on an asset are often considered part of the same asset class as the underlying instrument but are subject to different regulations than the underlying instrument. Many investment funds are composed of the two main asset classes, both of which are securities: equities (stocks) and fixed-income (bonds). However, some also hold cash and foreign currencies. Funds may also hold money market instruments and they may even refer to these as cash equivalents; however, that ignores the possibility of default. Money market instruments, being short-term fixed income investme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capital Asset Pricing Model
In finance, the capital asset pricing model (CAPM) is a model used to determine a theoretically appropriate required rate of return of an asset, to make decisions about adding assets to a well-diversified portfolio. The model takes into account the asset's sensitivity to non-diversifiable risk (also known as systematic risk or market risk), often represented by the quantity beta (β) in the financial industry, as well as the expected return of the market and the expected return of a theoretical risk-free asset. CAPM assumes a particular form of utility functions (in which only first and second moments matter, that is risk is measured by variance, for example a quadratic utility) or alternatively asset returns whose probability distributions are completely described by the first two moments (for example, the normal distribution) and zero transaction costs (necessary for diversification to get rid of all idiosyncratic risk). Under these conditions, CAPM shows that the cost of eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
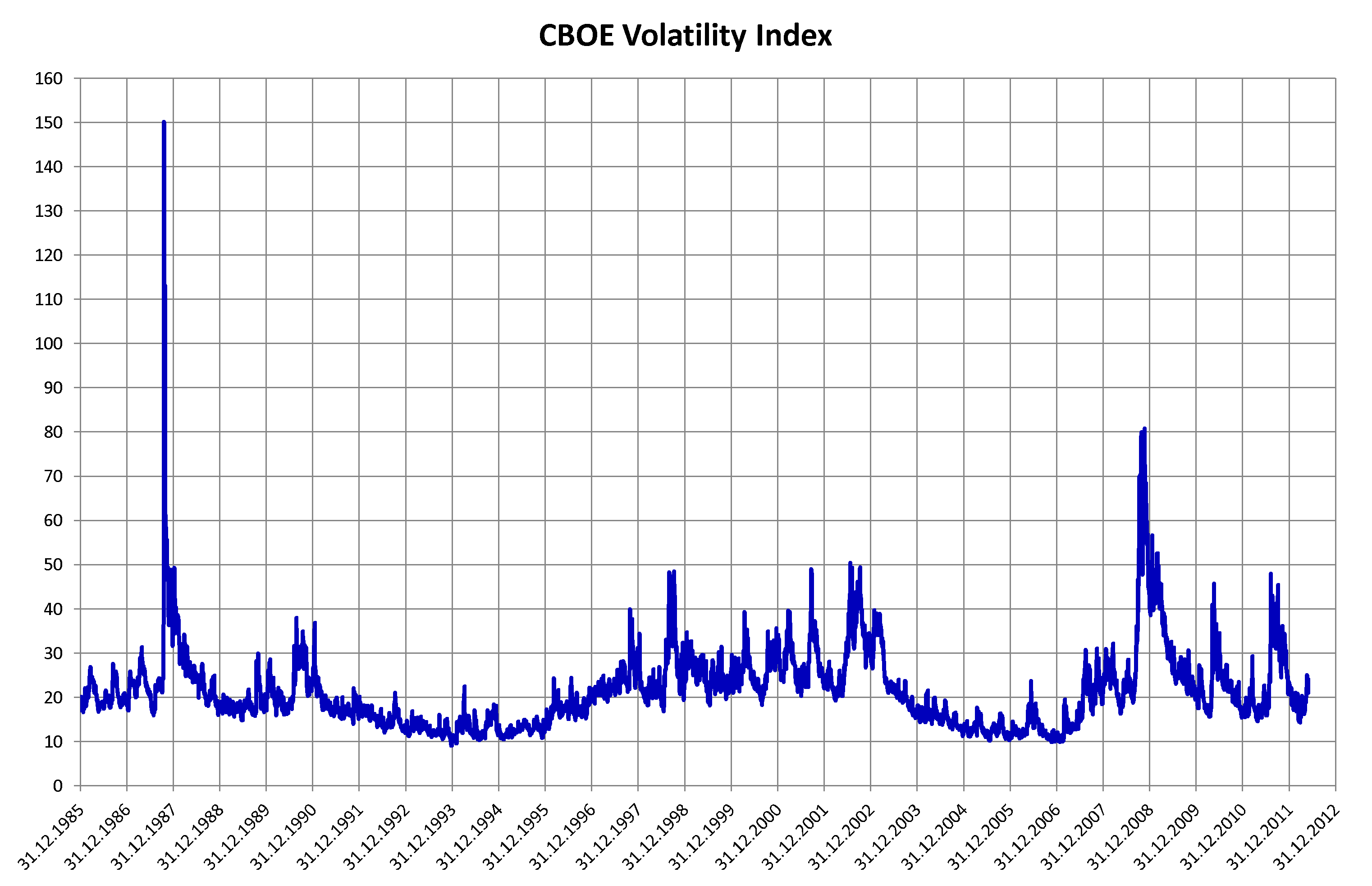
Volatility (finance)
In finance, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of squ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are ''linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
_-_Galton_1889_diagram.png)