|
Bell Shaped Function
A bell-shaped function or simply 'bell curve' is a mathematical function having a characteristic "bell"-shaped curve. These functions are typically continuous or smooth, asymptotically approach zero for large negative/positive x, and have a single, unimodal maximum at small x. Hence, the integral of a bell-shaped function is typically a sigmoid function. Bell shaped functions are also commonly symmetric. Many common probability distribution functions are bell curves. Some bell shaped functions, such as the Gaussian function and the probability distribution of the Cauchy distribution, can be used to construct sequences of functions with decreasing variance that approach the Dirac delta distribution. Indeed, the Dirac delta can roughly be thought of as a bell curve with variance tending to zero. Some examples include: * Gaussian function, the probability density function of the normal distribution. This is the archetypal bell shaped function and is frequently encountered in nat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution PDF
Normal(s) or The Normal(s) may refer to: Film and television * Normal (2003 film), ''Normal'' (2003 film), starring Jessica Lange and Tom Wilkinson * Normal (2007 film), ''Normal'' (2007 film), starring Carrie-Anne Moss, Kevin Zegers, Callum Keith Rennie, and Andrew Airlie * Normal (2009 film), ''Normal'' (2009 film), an adaptation of Anthony Neilson's 1991 play ''Normal: The Düsseldorf Ripper'' * ''Normal!'', a 2011 Algerian film * The Normals (film), ''The Normals'' (film), a 2012 American comedy film * Normal (New Girl), "Normal" (''New Girl''), an episode of the TV series Mathematics * Normal (geometry), an object such as a line or vector that is perpendicular to a given object * Normal basis (of a Galois extension), used heavily in cryptography * Normal bundle * Normal cone, of a subscheme in algebraic geometry * Normal coordinates, in differential geometry, local coordinates obtained from the exponential map (Riemannian geometry) * Normal distribution, the Gaussian continuo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Witch Of Agnesi
Witchcraft is the use of magic by a person called a witch. Traditionally, "witchcraft" means the use of magic to inflict supernatural harm or misfortune on others, and this remains the most common and widespread meaning. According to ''Encyclopedia Britannica'', "Witchcraft thus defined exists more in the imagination", but it "has constituted for many cultures a viable explanation of evil in the world". The belief in witches has been found throughout history in a great number of societies worldwide. Most of these societies have used protective magic or counter-magic against witchcraft, and have shunned, banished, imprisoned, physically punished or killed alleged witches. Anthropologists use the term "witchcraft" for similar beliefs about harmful occult practices in different cultures, and these societies often use the term when speaking in English. Belief in witchcraft as malevolent magic is attested from ancient Mesopotamia, and in Europe, belief in witches traces back ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Tangent Function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. 32 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Function
A logistic function or logistic curve is a common S-shaped curve ( sigmoid curve) with the equation f(x) = \frac where The logistic function has domain the real numbers, the limit as x \to -\infty is 0, and the limit as x \to +\infty is L. The exponential function with negated argument (e^ ) is used to define the standard logistic function, depicted at right, where L=1, k=1, x_0=0, which has the equation f(x) = \frac and is sometimes simply called the sigmoid. It is also sometimes called the expit, being the inverse function of the logit. The logistic function finds applications in a range of fields, including biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, statistics, and artificial neural networks. There are various generalizations, depending on the field. History The logistic function was introduced in a series of three papers by Pier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kaiser Window
The Kaiser window, also known as the Kaiser–Bessel window, was developed by James Kaiser at Bell Laboratories. It is a one-parameter family of window functions used in finite impulse response filter design and spectral estimation, spectral analysis. The Kaiser window approximates the DPSS window which Spectral concentration problem, maximizes the energy concentration in the main lobe but which is difficult to compute. Definition The Kaiser window and its Fourier transform are given by: : w_0(x) \triangleq \left\ \quad \stackrel\quad \frac , where: * is the zeroth-order Modified_Bessel_function#Modified_Bessel_functions:_Iα,_Kα, modified Bessel function of the first kind, * is the window duration, and * is a non-negative real number that determines the shape of the window. In the frequency domain, it determines the trade-off between main-lobe width and side lobe level, which is a central decision in window design. * Sometimes the Kaiser window is parametrized b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Window Function
In signal processing and statistics, a window function (also known as an apodization function or tapering function) is a mathematical function that is zero-valued outside of some chosen interval. Typically, window functions are symmetric around the middle of the interval, approach a maximum in the middle, and taper away from the middle. Mathematically, when another function or waveform/data-sequence is "multiplied" by a window function, the product is also zero-valued outside the interval: all that is left is the part where they overlap, the "view through the window". Equivalently, and in actual practice, the segment of data within the window is first isolated, and then only that data is multiplied by the window function values. Thus, tapering, not segmentation, is the main purpose of window functions. The reasons for examining segments of a longer function include detection of transient events and time-averaging of frequency spectra. The duration of the segments is determine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raised-cosine Filter
The raised-cosine filter is a filter frequently used for pulse-shaping in digital modulation due to its ability to minimise intersymbol interference (ISI). Its name stems from the fact that the non-zero portion of the frequency spectrum of its simplest form (\beta = 1) is a cosine function, 'raised' up to sit above the f (horizontal) axis. Mathematical description The raised-cosine filter is an implementation of a low-pass Nyquist filter, i.e., one that has the property of vestigial symmetry. This means that its spectrum exhibits odd symmetry about \frac, where T is the symbol-period of the communications system. Its frequency-domain description is a piecewise-defined function, given by: :H(f) = \begin 1, & , f, \leq \frac \\ \frac\left [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raised Cosine Distribution
In probability theory and statistics, the raised cosine distribution is a continuous probability distribution supported on the interval mu-s,\mu+s/math>. The probability density function (PDF) is :f(x;\mu,s)=\frac \left +\cos\left(\frac\,\pi\right)\right,=\frac\operatorname\left(\frac\,\pi\right) \text \mu-s\le x\le\mu+s and zero otherwise. The cumulative distribution function (CDF) is :F(x;\mu,s)=\frac\left +\frac + \frac \sin\left(\frac \, \pi \right) \right/math> for \mu-s \le x \le \mu+s and zero for x\mu+s. The moments of the raised cosine distribution are somewhat complicated in the general case, but are considerably simplified for the standard raised cosine distribution. The standard raised cosine distribution is just the raised cosine distribution with \mu=0 and s=1. Because the standard raised cosine distribution is an even function, the odd moments are zero. The even moments are given by: : \begin \operatorname E(x^) & = \frac\int_^1 +\cos(x\pi)^\,dx = \int_^1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bump Function
In mathematical analysis, a bump function (also called a test function) is a function f : \Reals^n \to \Reals on a Euclidean space \Reals^n which is both smooth (in the sense of having continuous derivatives of all orders) and compactly supported. The set of all bump functions with domain \Reals^n forms a vector space, denoted \mathrm^\infty_0(\Reals^n) or \mathrm^\infty_\mathrm(\Reals^n). The dual space of this space endowed with a suitable topology is the space of distributions. Examples The function \Psi : \mathbb \to \mathbb given by \Psi(x) = \begin \exp\left( \frac\right), & \text , x, . In fact, by definition of support, we have that \operatorname(\Psi):=\overline =\overline, where the closure is taken with respect the Euclidean topology of the real line. The proof of smoothness follows along the same lines as for the related function discussed in the Non-analytic smooth function article. This function can be interpreted as the Gaussian function \exp\le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arctangent
In mathematics, the inverse trigonometric functions (occasionally also called ''antitrigonometric'', ''cyclometric'', or ''arcus'' functions) are the inverse functions of the trigonometric functions, under suitably restricted domains. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry. Notation Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: , , , etc. (This convention is used throughout this article.) This notation arises from the following geometric relationships: when measuring in radians, an angle of radians will correspond to an arc whose length is , where is the radius of the circle. Thus in the unit circle, the cosine of x f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
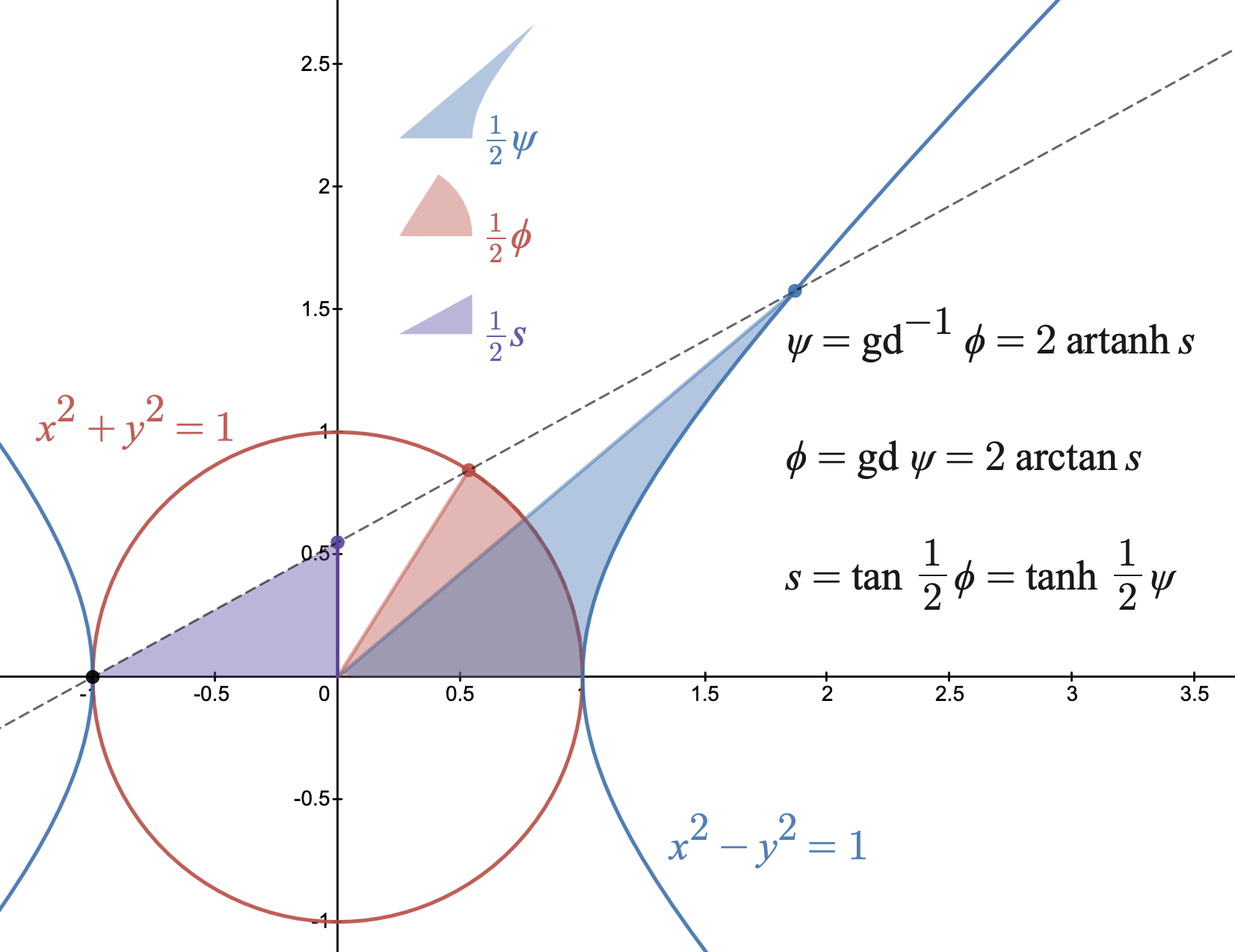
Gudermannian Function
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant : The real inverse Gudermannian function can be defined for |