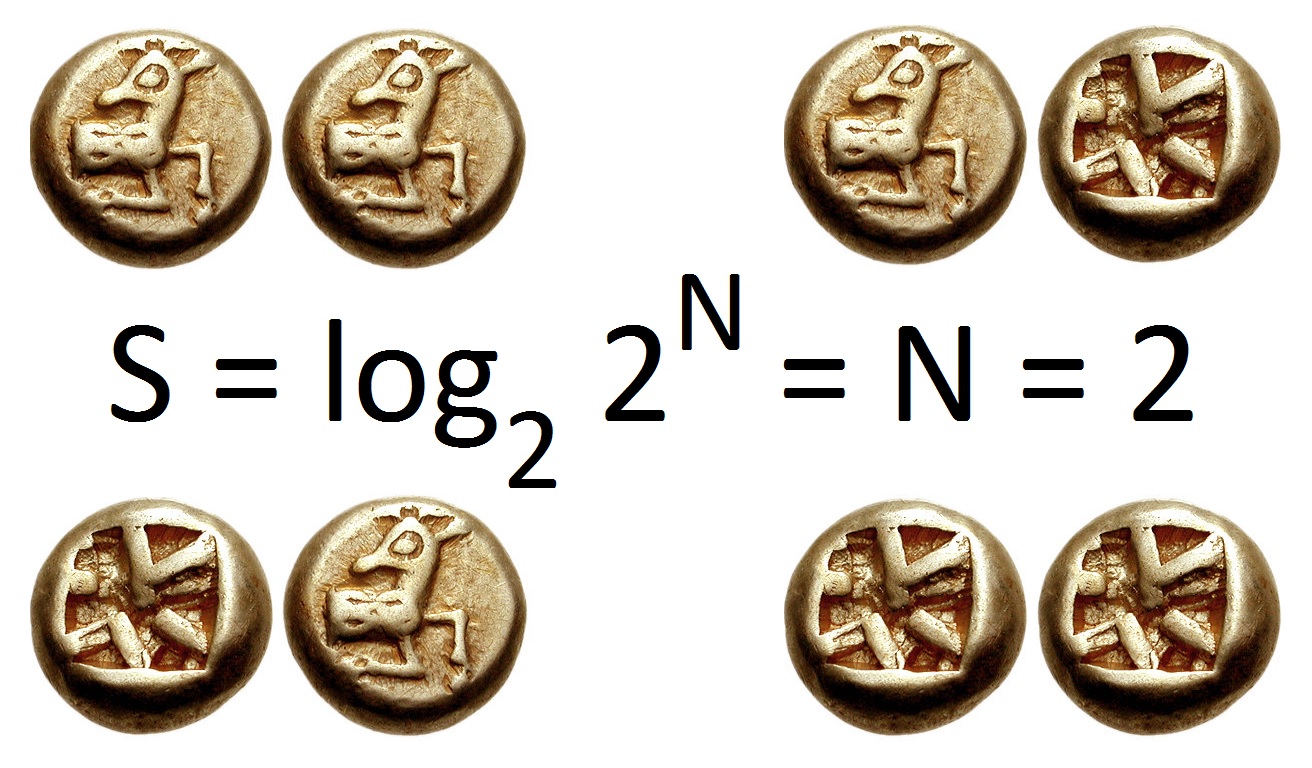|
Arithmetic Coder
Arithmetic coding (AC) is a form of entropy encoding used in lossless data compression. Normally, a string of characters is represented using a fixed number of bits per character, as in the ASCII code. When a string is converted to arithmetic encoding, frequently used characters will be stored with fewer bits and not-so-frequently occurring characters will be stored with more bits, resulting in fewer bits used in total. Arithmetic coding differs from other forms of entropy encoding, such as Huffman coding, in that rather than separating the input into component symbols and replacing each with a code, arithmetic coding encodes the entire message into a single number, an arbitrary-precision fraction ''q'', where . It represents the current information as a range, defined by two numbers. A recent family of entropy coders called asymmetric numeral systems allows for faster implementations thanks to directly operating on a single natural number representing the current information., bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Entropy Encoding
In information theory, an entropy coding (or entropy encoding) is any lossless data compression method that attempts to approach the lower bound declared by Shannon's source coding theorem, which states that any lossless data compression method must have an expected code length greater than or equal to the entropy of the source. More precisely, the source coding theorem states that for any source distribution, the expected code length satisfies \operatorname E_ ell(d(x))\geq \operatorname E_ \log_b(P(x))/math>, where \ell is the function specifying the number of symbols in a code word, d is the coding function, b is the number of symbols used to make output codes and P is the probability of the source symbol. An entropy coding attempts to approach this lower bound. Two of the most common entropy coding techniques are Huffman coding and arithmetic coding. If the approximate entropy characteristics of a data stream are known in advance (especially for signal compression), a simple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Information Entropy
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to , 1/math>, the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stanford University
Leland Stanford Junior University, commonly referred to as Stanford University, is a Private university, private research university in Stanford, California, United States. It was founded in 1885 by railroad magnate Leland Stanford (the eighth List of governors of California, governor of and then-incumbent List of United States senators from California, United States senator representing California) and his wife, Jane Stanford, Jane, in memory of their only child, Leland Stanford Jr., Leland Jr. The university admitted its first students in 1891, opening as a Mixed-sex education, coeducational and non-denominational institution. It struggled financially after Leland died in 1893 and again after much of the campus was damaged by the 1906 San Francisco earthquake. Following World War II, university Provost (education), provost Frederick Terman inspired an entrepreneurship, entrepreneurial culture to build a self-sufficient local industry (later Silicon Valley). In 1951, Stanfor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
IBM Research
IBM Research is the research and development division for IBM, an American Multinational corporation, multinational information technology company. IBM Research is headquartered at the Thomas J. Watson Research Center in Yorktown Heights, New York, near IBM headquarters in Armonk, New York. It is the largest industrial research organization in the world with operations in over 170 countries and twelve labs on six continents. IBM employees have garnered six Nobel Prizes, six Turing Awards, 20 inductees into the U.S. National Inventors Hall of Fame, 19 National Medal of Technology, National Medals of Technology, five National Medal of Science, National Medals of Science and three Kavli Foundation (United States)#The Kavli Prize, Kavli Prizes. , the company has generated more patents than any other business in each of 25 consecutive years, which is a record. History The roots of today's IBM Research began with the 1945 opening of the Watson Scientific Computing Laboratory at Columbi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bernoulli Process
In probability and statistics, a Bernoulli process (named after Jacob Bernoulli) is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables ''X''''i'' are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin (but with consistent unfairness). Every variable ''X''''i'' in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes (such as the process for a six-sided die); this generalization is known as the Bernoulli scheme. The problem of determining the process, given only a limited sample of Bernoulli trials, may be called the problem of checking whether a coin is fair. Definition A ''Bernoulli process'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Golomb Coding
Golomb coding is a lossless data compression method using a family of data compression codes invented by Solomon W. Golomb in the 1960s. Alphabets following a geometric distribution will have a Golomb code as an optimal prefix code, making Golomb coding highly suitable for situations in which the occurrence of small values in the input stream is significantly more likely than large values. Rice coding Rice coding (invented by Robert F. Rice) denotes using a subset of the family of Golomb codes to produce a simpler (but possibly suboptimal) prefix code. Rice used this set of codes in an adaptive coding scheme; "Rice coding" can refer either to that adaptive scheme or to using that subset of Golomb codes. Whereas a Golomb code has a tunable parameter that can be any positive integer value, Rice codes are those in which the tunable parameter is a power of two. This makes Rice codes convenient for use on a computer, since multiplication and division by 2 can be implemented ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Run-length Encoding
Run-length encoding (RLE) is a form of lossless data compression in which ''runs'' of data (consecutive occurrences of the same data value) are stored as a single occurrence of that data value and a count of its consecutive occurrences, rather than as the original run. As an imaginary example of the concept, when encoding an image built up from colored dots, the sequence "green green green green green green green green green" is shortened to "green x 9". This is most efficient on data that contains many such runs, for example, simple graphic images such as icons, line drawings, games, and animations. For files that do not have many runs, encoding them with RLE could increase the file size. RLE may also refer in particular to an early graphics file format supported by CompuServe for compressing black and white images, that was widely supplanted by their later Graphics Interchange Format (GIF). RLE also refers to a little-used image format in Windows 3.x that is saved with the fil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Independent And Identically Distributed Random Variables
Independent or Independents may refer to: Arts, entertainment, and media Artist groups * Independents (artist group), a group of modernist painters based in Pennsylvania, United States * Independentes (English: Independents), a Portuguese artist group Music Groups, labels, and genres * Independent music, a number of genres associated with independent labels * Independent record label, a record label not associated with a major label * Independent Albums, American albums chart Albums * ''Independent'' (Ai album), 2012 * ''Independent'' (Faze album), 2006 * ''Independent'' (Sacred Reich album), 1993 Songs * "Independent" (song), a 2007 song by Webbie * "Independent", a 2002 song by Ayumi Hamasaki from '' H'' News media organizations * Independent Media Center (also known as Indymedia or IMC), an open publishing network of journalist collectives that report on political and social issues, e.g., in ''The Indypendent'' newspaper of NYC * ITV (TV network) (Independent Televi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Asymptotic Equipartition Property
In information theory, the asymptotic equipartition property (AEP) is a general property of the output samples of a stochastic source. It is fundamental to the concept of typical set used in theories of data compression. Roughly speaking, the theorem states that although there are many series of results that may be produced by a random process, the one actually produced is most probably from a loosely defined set of outcomes that all have approximately the same chance of being the one actually realized. (This is a consequence of the law of large numbers and ergodic theory.) Although there are individual outcomes which have a higher probability than any outcome in this set, the vast number of outcomes in the set almost guarantees that the outcome will come from the set. One way of intuitively understanding the property is through Cramér's large deviation theorem, which states that the probability of a large deviation from mean decays exponentially with the number of samples. Suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Entropy (information Theory)
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to[0, 1], the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or "shannon (unit), shannons"), while base Euler's number, ''e'' gives "natural units" nat (unit), nat, and base 10 gives units of "dits", "bans", or "Hartley (unit), hartleys". An equivalent definition of entropy is the expected value of the self-information of a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |