|
Area Hyperbolic Tangent
In mathematics, the inverse hyperbolic functions are the inverse functions of the hyperbolic functions. For a given value of a hyperbolic function, the corresponding inverse hyperbolic function provides the corresponding hyperbolic angle. The size of the hyperbolic angle is equal to the area of the corresponding hyperbolic sector of the hyperbola , or twice the area of the corresponding sector of the unit hyperbola , just as a circular angle is twice the area of the circular sector of the unit circle. Some authors have called inverse hyperbolic functions "area functions" to realize the hyperbolic angles. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. It also occurs in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Functions-2
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry. The following phenomena are described as ''hyperbolic'' because they manifest hyperbolas, not because something about them is exaggerated. * Hyperbolic angle, an unbounded variable referring to a hyperbola instead of a circle * Hyperbolic coordinates, location by geometric mean and hyperbolic angle in quadrant I * Hyperbolic distribution, a probability distribution characterized by the logarithm of the probability density function being a hyperbola * Hyperbolic equilibrium point, a fixed point that does not have any center manifolds * Hyperbolic function, an analog of an ordinary trigonometric or circular function * Hyperbolic geometric graph, a random network generated by connecting nearby points sprinkled in a hyperbolic space * Hyperbolic geometry, a non-Euclidean geometry * Hyperbolic group, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Function
In mathematics, a cubic function is a function of the form f(x)=ax^3+bx^2+cx+d where the coefficients , , , and are complex numbers, and the variable takes real values, and a\neq 0. In other words, it is both a polynomial function of degree three, and a real function. In particular, the domain and the codomain are the set of the real numbers. Setting produces a cubic equation of the form :ax^3+bx^2+cx+d=0, whose solutions are called roots of the function. A cubic function has either one or three real roots (which may not be distinct); all odd-degree polynomials have at least one real root. The graph of a cubic function always has a single inflection point. It may have two critical points, a local minimum and a local maximum. Otherwise, a cubic function is monotonic. The graph of a cubic function is symmetric with respect to its inflection point; that is, it is invariant under a rotation of a half turn around this point. Up to an affine transformation, there are only th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxford Users' Guide To Mathematics
Oxford () is a city in England. It is the county town and only city of Oxfordshire. In 2020, its population was estimated at 151,584. It is north-west of London, south-east of Birmingham and north-east of Bristol. The city is home to the University of Oxford, the oldest university in the English-speaking world; it has buildings in every style of English architecture since late Anglo-Saxon. Oxford's industries include motor manufacturing, education, publishing, information technology and science. History The history of Oxford in England dates back to its original settlement in the Saxon period. Originally of strategic significance due to its controlling location on the upper reaches of the River Thames at its junction with the River Cherwell, the town grew in national importance during the early Norman period, and in the late 12th century became home to the fledgling University of Oxford. The city was besieged during The Anarchy in 1142. The university rose t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wolfgang Hackbusch
Wolfgang Hackbusch (born 24 October 1948 in Westerstede, Lower Saxony) is a German mathematician, known for his pioneering research in multigrid methods and later hierarchical matrices, a concept generalizing the fast multipole method. He was a professor at the University of Kiel and is currently one of the directors of the Max Planck Institute for Mathematics in the Sciences in Leipzig. Awards and honors * 1994 Gottfried Wilhelm Leibniz Prize * 1996 Brouwer Medal * 1998 Plenary Speaker of the International Congress of Mathematicians The International Congress of Mathematicians (ICM) is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union (IMU). The Fields Medals, the Nevanlinna Prize (to be rename ... Publications * Multi-grid methods and applications, 1985, Springer Berlin, 2013 pbk reprint* Elliptic Differential Equations: Theory and Numerical Treatment, 1992, Springer Berlin, * Iterati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eberhard Zeidler (mathematician)
Eberhard Hermann Erich Zeidler (6 October 1940 in Leipzig, Germany – 18 November 2016 ibid) was a German mathematician, who worked primarily in the field of non-linear functional analysis. Life and work After attending the Leipzig Eberhard Zeidler began studying mathematics at the University of Leipzig in 1959. In 1961, he was exmatriculated because of critical statements, and was forced to work as a transport worker and absolve his military service in the East-German's NVA. In 1964, he was allowed to continue his studies. In 1967, he received his Dr. rer. nat. (PhD) with his work "" under . In 1970, he was appointed to habilitation and became a lecturer for analysis at the University of Leipzig. From 1974 to 1996 he was full professor for analysis. In the winter semester of 1979–1980, Eberhard Zeidler was a visiting professor at the University of Wisconsin–Madison (USA). From 1992 to 1996, he was head of the DFG research group on "" (Nonlinear functional analysis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jan Gullberg
Jan Gullberg (1936 – 21 May 1998) was a Swedish surgeon and anaesthesiologist, but became known as a writer on popular science and medical topics. He is best known outside Sweden as the author of ''Mathematics: From the Birth of Numbers'', published by W. W. Norton in 1997 (). Life Gullberg grew up and was trained as a surgeon in Sweden. He qualified in medicine at the University of Lund in 1964. He practised as a surgeon in Saudi Arabia, Norway and Virginia Mason Hospital, Seattle in the United States, as well as in Sweden. Gullberg saw himself as a doctor rather than a writer. His first book, on science, won the Swedish Medical Society's Jubilee Prize in 1980, and saw him promoted to honorary doctor at the University of Lund the same year. He was twice married: first to Anne-Marie Hallin (d. 1983), with whom he had three children; and Ann Richardson (b. 1951) with whom he adopted twin sons, Kamen and Kalin. He died of a stroke in Nordfjordeid, Norway at the hospital where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Trigonometric Functions
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted Domain of a function, domains). Specifically, they are the inverses of the sine, cosine, tangent (trigonometry), tangent, cotangent, secant (trigonometry), secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry. Notation Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: , , , etc. (This convention is used throughout this article.) This notation arises from the following geometric relationships: when measuring in radians, an angle of ''θ'' radians will correspond to an arc whose length is ''rθ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ISO 80000-2
ISO 80000 or IEC 80000 is an international standard introducing the International System of Quantities (ISQ). It was developed and promulgated jointly by the International Organization for Standardization (ISO) and the International Electrotechnical Commission (IEC). It serves as a style guide for the use of physical quantities and units of measurement, formulas involving them, and their corresponding units, in scientific and educational documents for worldwide use. The ISO/IEC 80000 family of standards was completed with the publication of Part 1 in November 2009. Overview , ISO/IEC 80000 comprises 13 parts, two of which (parts 6 and 13) were developed by IEC and the remaining 11 were developed by ISO, with a further three parts (15, 16 and 17) under development. Part 14 was withdrawn. Subject areas The 80000 standard currently has 13 parts. Part 1: General ISO 80000-1:2009 replaces ISO 31-0:1992 and ISO 1000:1992. It gives general information and definitions con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates: # The laws of physics are invariant (that is, identical) in all inertial frames of reference (that is, frames of reference with no acceleration). # The speed of light in vacuum is the same for all observers, regardless of the motion of the light source or the observer. Origins and significance Special relativity was originally proposed by Albert Einstein in a paper published on 26 September 1905 titled "On the Electrodynamics of Moving Bodies".Albert Einstein (1905)''Zur Elektrodynamik bewegter Körper'', ''Annalen der Physik'' 17: 891; English translatioOn the Electrodynamics of Moving Bodiesby George Barker Jeffery and Wilfrid Perrett (1923); Another English translation On the Electrodynamics of Moving Bodies by Megh Nad Saha (1920). The incompa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
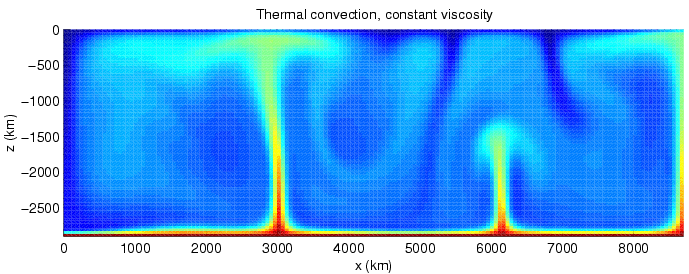
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space and time. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, Convection (heat transfer), thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species (mass transfer in the form of advection), either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system. Heat conduction, also called diffusion, is the direct microscopic exchanges of kinetic energy of particles (such as molecules) or quasiparticles (such as lattice waves) through the boundary between two systems. When an object is at a different temperature from another body or its surroundings, heat flows so that the body and the surroundings reach the same temperature, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetic Theory
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions of atoms and molecules. Electromagnetism can be thought of as a combination of electricity and magnetism, two distinct but closely intertwined phenomena. In essence, electric forces occur between any two charged particles, causing an attraction between particles with opposite charges and repulsion between particles with the same charge, while magnetism is an interaction that occurs exclusively between ''moving'' charged particles. These two effects combine to create electromagnetic fields in the vicinity of charge particles, which can exert influence on other particles via the Lorentz force. At high energy, the weak force and electromagnetic force are unified as a single electroweak force. The electromagnetic force is responsible for many o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |