|
Applied Element Method
The applied element method (AEM) is a numerical analysis used in predicting the continuum and discrete behavior of structures. The modeling method in AEM adopts the concept of discrete cracking allowing it to automatically track structural collapse behavior passing through all stages of loading: elastic, crack initiation and propagation in tension-weak materials, reinforcement yield, element separation, element contact and collision, as well as collision with the ground and adjacent structures. History Exploration of the approach employed in the applied element method began in 1995 at the University of Tokyo as part of Dr. Hatem Tagel-Din's research studies. The term "applied element method" itself, however, was first coined in 2000 in a paper called "Applied element method for structural analysis: Theory and application for linear materials". Since then AEM has been the subject of research by a number of academic institutions and the driving factor in real-world applications. Re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Continuum
In the mathematical field of order theory, a continuum or linear continuum is a generalization of the real line. Formally, a linear continuum is a linearly ordered set ''S'' of more than one element that is densely ordered, i.e., between any two distinct elements there is another (and hence infinitely many others), and complete, i.e., which "lacks gaps" in the sense that every nonempty subset with an upper bound has a least upper bound. More symbolically: ''S'' has the least upper bound property, and For each ''x'' in ''S'' and each ''y'' in ''S'' with ''x'' < ''y'', there exists ''z'' in ''S'' such that ''x'' < ''z'' < ''y'' A has the least upper bound property, if every nonempty subset of the set that is bounded above has a least upper bound in the set. Linear continua are particularly important in the field of |
Deformation (mechanics)
In physics, deformation is the continuum mechanics transformation of a body from a ''reference'' configuration to a ''current'' configuration. A configuration is a set containing the positions of all particles of the body. A deformation can occur because of external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. Strain is related to deformation in terms of ''relative'' displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered. In a continuous body, a deformation field results from a stress field due to applied forces or because of some changes in the temperature field of the body. The rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forensic Engineering
Forensic engineering has been defined as ''"the investigation of failures - ranging from serviceability to catastrophic - which may lead to legal activity, including both civil and criminal".'' It includes the investigation of materials, products, structures or components that fail or do not operate or function as intended, causing personal injury, damage to property or economic loss. The consequences of failure may give rise to action under either criminal or civil law including but not limited to health and safety legislation, the laws of contract and/or product liability and the laws of tort. The field also deals with retracing processes and procedures leading to accidents in operation of vehicles or machinery. Generally, the purpose of a forensic engineering investigation is to locate cause or causes of failure with a view to improve performance or life of a component, or to assist a court in determining the facts of an accident. It can also involve investigation of intellect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismic Analysis
Seismic analysis is a subset of structural analysis and is the calculation of the response of a building (or nonbuilding) structure to earthquakes. It is part of the process of structural design, earthquake engineering or structural assessment and retrofit (see structural engineering) in regions where earthquakes are prevalent. As seen in the figure, a building has the potential to 'wave' back and forth during an earthquake (or even a severe wind storm). This is called the 'fundamental mode', and is the lowest frequency of building response. Most buildings, however, have higher modes of response, which are uniquely activated during earthquakes. The figure just shows the second mode, but there are higher 'shimmy' (abnormal vibration) modes. Nevertheless, the first and second modes tend to cause the most damage in most cases. The earliest provisions for seismic resistance were the requirement to design for a lateral force equal to a proportion of the building weight (appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Progressive Collapse
Progressive collapse is the process where a primary structural element fails, resulting in the failure of adjoining structural elements, which in turn causes further structural failure. Progressive collapses may be accidental, as the result of design deficiencies, fire, unintentional overload, material failure or natural phenomenon (e.g. erosion, wind or earthquakes). They can also be induced deliberately as a demolition method, specifically that of building implosion, or caused by acts of terrorism or war. Notable examples * On July 14, 1902, the 98 m (323-foot) St Mark's Campanile in Venice, Italy collapsed after its northern load-bearing wall began to separate from the main structure. The cause of the separation was attributed to more than 700 years of wear on the structure, including fires, earthquakes, and stress redistribution, primarily from drying-induced shrinkage on the wooden support beams, the bells swaying back and forth, and creep. No one was injured except fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Load
A structural load or structural action is a force, deformation, or acceleration applied to structural elements. A load causes stress, deformation, and displacement in a structure. Structural analysis, a discipline in engineering, analyzes the effects of loads on structures and structural elements. Excess load may cause structural failure, so this should be considered and controlled during the design of a structure. Particular mechanical structures—such as aircraft, satellites, rockets, space stations, ships, and submarines—are subject to their own particular structural loads and actions. Engineers often evaluate structural loads based upon published regulations, contracts, or specifications. Accepted technical standards are used for acceptance testing and inspection. Types Dead loads are static forces that are relatively constant for an extended time. They can be in tension or compression. The term can refer to a laboratory test method or to the normal usage of a material ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stiffness Matrix
In the finite element method for the numerical solution of elliptic partial differential equations, the stiffness matrix is a matrix that represents the system of linear equations that must be solved in order to ascertain an approximate solution to the differential equation. The stiffness matrix for the Poisson problem For simplicity, we will first consider the Poisson problem : -\nabla^2 u = f on some domain , subject to the boundary condition on the boundary of . To discretize this equation by the finite element method, one chooses a set of ''basis functions'' defined on which also vanish on the boundary. One then approximates : u \approx u^h = u_1\varphi_1+\cdots+u_n\varphi_n. The coefficients are determined so that the error in the approximation is orthogonal to each basis function : : \int_\Omega \varphi_i\cdot f \, dx = -\int_\Omega \varphi_i\nabla^2u^h \, dx = -\sum_j\left(\int_\Omega \varphi_i\nabla^2\varphi_j\,dx\right)\, u_j = \sum_j\left(\int_\Omega \nabla\var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in ''n''-dimensional Euclidean space. In geometry, one often assumes uniform mass density, in which case the ''barycenter'' or ''center of mass'' coincides with the centroid. Informally, it can be understood as the point at which a cutout of the shape (with uniformly distributed mass) could be perfectly balanced on the tip of a pin. In physics, if variations in gravity are considered, then a ''center of gravity'' can be defined as the weighted mean of all points weighted by their specific weight. In geography, the centroid of a radial projection of a region of the Earth's surface to sea level is the region's geographical center. History The term "centroid" is of recent coinage (1814). It is used as a substitute for the older te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Displacement (vector)
In geometry and mechanics, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion. It quantifies both the distance and direction of the net or total motion along a straight line from the initial position to the final position of the point trajectory. A displacement may be identified with the translation that maps the initial position to the final position. A displacement may be also described as a '' relative position'' (resulting from the motion), that is, as the final position of a point relative to its initial position . The corresponding displacement vector can be defined as the difference between the final and initial positions: s = x_\textrm - x_\textrm = \Delta In considering motions of objects over time, the instantaneous velocity of the object is the rate of change of the displacement as a function of time. The instantaneous speed, then, is distinct from velocity, or the time rate of chan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (physics And Chemistry)
In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space. The location of a particle in three-dimensional space requires three position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is deterministic (where the state at one instant uniquely determines its past and future position and velocity as a function of time) such a system has six degrees of freedom. If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer than six degrees of freedom. On the oth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
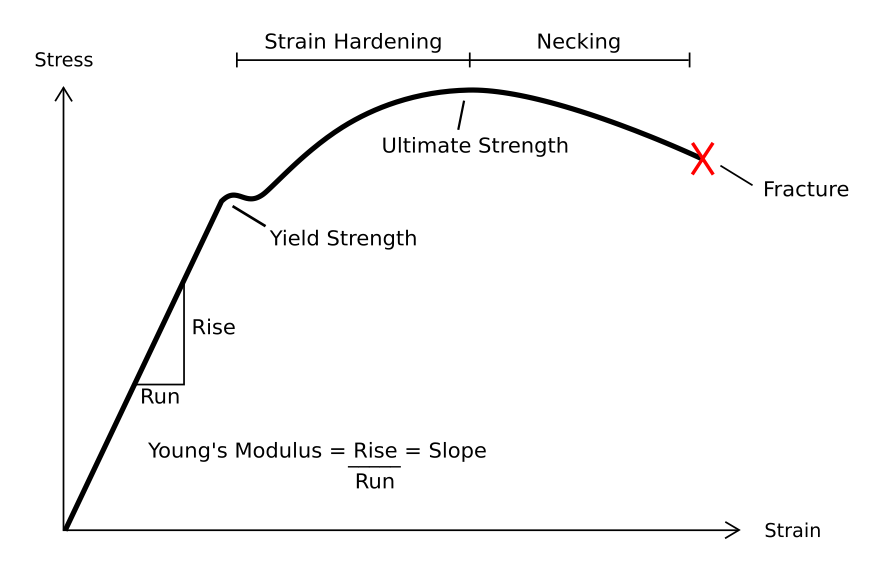
Deformation (engineering)
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a structure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rigid Body
In physics, a rigid body (also known as a rigid object) is a solid body in which deformation is zero or so small it can be neglected. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass. In the study of special relativity, a perfectly rigid body does not exist; and objects can only be assumed to be rigid if they are not moving near the speed of light. In quantum mechanics, a rigid body is usually thought of as a collection of point masses. For instance, molecules (consisting of the point masses: electrons and nuclei) are often seen as rigid bodies (see classification of molecules as rigid rotors). Kinematics Linear and angular position The position of a rigid body is the position of all the particles of which it is composed. To simplify the description of this position, we exploit the property that the body is rigi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |