|
Algebraically Closed Group
In group theory, a group A\ is algebraically closed if any finite set of equations and inequations that are applicable to A\ have a solution in A\ without needing a group extension. This notion will be made precise later in the article in . Informal discussion Suppose we wished to find an element x\ of a group G\ satisfying the conditions (equations and inequations): ::x^2=1\ ::x^3=1\ ::x\ne 1\ Then it is easy to see that this is impossible because the first two equations imply x=1\ . In this case we say the set of conditions are inconsistent with G\ . (In fact this set of conditions are inconsistent with any group whatsoever.) Now suppose G\ is the group with the multiplication table to the right. Then the conditions: ::x^2=1\ ::x\ne 1\ have a solution in G\ , namely x=a\ . However the conditions: ::x^4=1\ ::x^2a^ = 1\ Do not have a solution in G\ , as can easily be checked. However if we extend the group G \ to the group H \ with the adjacent multiplic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field (mathematics), fields, and vector spaces, can all be seen as groups endowed with additional operation (mathematics), operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, and Standard Model, three of the four known fundamental forces in the universe, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set and an Binary operation, operation that combines any two Element (mathematics), elements of the set to produce a third element of the set, in such a way that the operation is Associative property, associative, an identity element exists and every element has an Inverse element, inverse. These three axioms hold for Number#Main classification, number systems and many other mathematical structures. For example, the integers together with the addition operation form a group. The concept of a group and the axioms that define it were elaborated for handling, in a unified way, essential structural properties of very different mathematical entities such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry groups arise naturally in the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
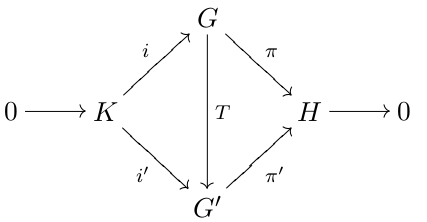
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the center o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inconsistent
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if it has a model, i.e., there exists an interpretation under which all formulas in the theory are true. This is the sense used in traditional Aristotelian logic, although in contemporary mathematical logic the term ''satisfiable'' is used instead. The syntactic definition states a theory T is consistent if there is no formula \varphi such that both \varphi and its negation \lnot\varphi are elements of the set of consequences of T. Let A be a set of closed sentences (informally "axioms") and \langle A\rangle the set of closed sentences provable from A under some (specified, possibly implicitly) formal deductive system. The set of axioms A is consistent when \varphi, \lnot \varphi \in \langle A \rangle for no formula \varphi. If there exis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Group
In mathematics, the free group ''F''''S'' over a given set ''S'' consists of all words that can be built from members of ''S'', considering two words to be different unless their equality follows from the group axioms (e.g. ''st'' = ''suu''−1''t'', but ''s'' ≠ ''t''−1 for ''s'',''t'',''u'' ∈ ''S''). The members of ''S'' are called generators of ''F''''S'', and the number of generators is the rank of the free group. An arbitrary group ''G'' is called free if it is isomorphic to ''F''''S'' for some subset ''S'' of ''G'', that is, if there is a subset ''S'' of ''G'' such that every element of ''G'' can be written in exactly one way as a product of finitely many elements of ''S'' and their inverses (disregarding trivial variations such as ''st'' = ''suu''−1''t''). A related but different notion is a free abelian group; both notions are particular instances of a free object from universal algebra. As such, free groups are defined by their universal property. History Free ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countably
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (its number of elements) is not greater than that of the natural numbers. A countable set that is not finite is said countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as defined here are quite com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Product
In mathematics, specifically group theory, the free product is an operation that takes two groups ''G'' and ''H'' and constructs a new The result contains both ''G'' and ''H'' as subgroups, is generated by the elements of these subgroups, and is the “universal” group having these properties, in the sense that any two homomorphisms from ''G'' and ''H'' into a group ''K'' factor uniquely through a homomorphism from to ''K''. Unless one of the groups ''G'' and ''H'' is trivial, the free product is always infinite. The construction of a free product is similar in spirit to the construction of a free group (the universal group with a given set of generators). The free product is the coproduct in the category of groups. That is, the free product plays the same role in group theory that disjoint union plays in set theory, or that the direct sum plays in module theory. Even if the groups are commutative, their free product is not, unless one of the two groups is the trivial grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countable
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (its number of elements) is not greater than that of the natural numbers. A countable set that is not finite is said countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as defined here are quite comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Group
SIMPLE Group Limited is a conglomeration of separately run companies that each has its core area in International Consulting. The core business areas are Legal Services, Fiduciary Activities, Banking Intermediation and Corporate Service. The date of incorporation is listed as 1999 by Companies House of Gibraltar, who class it as a holding company; however it is understood that SIMPLE Group's business and trading activities date to the second part of the 90s, probably as an incorporated body. SIMPLE Group Limited is a conglomerate that cultivate secrecy, they are not listed on any Stock Exchange and the group is owned by a complicated series of offshore trust An offshore trust is a conventional trust that is formed under the laws of an offshore jurisdiction. Generally offshore trusts are similar in nature and effect to their onshore counterparts; they involve a settlor transferring (or 'settling') a ...s. The Sunday Times stated that SIMPLE Group's interests could be eval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finitely Generated Group
In algebra, a finitely generated group is a group ''G'' that has some finite generating set ''S'' so that every element of ''G'' can be written as the combination (under the group operation) of finitely many elements of ''S'' and of inverses of such elements. By definition, every finite group is finitely generated, since ''S'' can be taken to be ''G'' itself. Every infinite finitely generated group must be countable but countable groups need not be finitely generated. The additive group of rational numbers Q is an example of a countable group that is not finitely generated. Examples * Every quotient of a finitely generated group ''G'' is finitely generated; the quotient group is generated by the images of the generators of ''G'' under the canonical projection. * A subgroup of a finitely generated group need not be finitely generated. * A group that is generated by a single element is called cyclic. Every infinite cyclic group is isomorphic to the additive group of the integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Presentation Of A Group
In mathematics, a presentation is one method of specifying a group. A presentation of a group ''G'' comprises a set ''S'' of generators—so that every element of the group can be written as a product of powers of some of these generators—and a set ''R'' of relations among those generators. We then say ''G'' has presentation :\langle S \mid R\rangle. Informally, ''G'' has the above presentation if it is the "freest group" generated by ''S'' subject only to the relations ''R''. Formally, the group ''G'' is said to have the above presentation if it is isomorphic to the quotient of a free group on ''S'' by the normal subgroup generated by the relations ''R''. As a simple example, the cyclic group of order ''n'' has the presentation :\langle a \mid a^n = 1\rangle, where 1 is the group identity. This may be written equivalently as :\langle a \mid a^n\rangle, thanks to the convention that terms that do not include an equals sign are taken to be equal to the group identity. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word Problem For Groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group ''G'' is the algorithmic problem of deciding whether two words in the generators represent the same element. More precisely, if ''A'' is a finite set of generators for ''G'' then the word problem is the membership problem for the formal language of all words in ''A'' and a formal set of inverses that map to the identity under the natural map from the free monoid with involution on ''A'' to the group ''G''. If ''B'' is another finite generating set for ''G'', then the word problem over the generating set ''B'' is equivalent to the word problem over the generating set ''A''. Thus one can speak unambiguously of the decidability of the word problem for the finitely generated group ''G''. The related but different uniform word problem for a class ''K'' of recursively presented groups is the algorithmic problem of deciding, given as input a pres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |