|
Acceptance Set
In financial mathematics, acceptance set is a set of acceptable future net worth which is acceptable to the regulator. It is related to risk measures. Mathematical Definition Given a probability space (\Omega,\mathcal,\mathbb), and letting L^p = L^p(\Omega,\mathcal,\mathbb) be the Lp space in the scalar case and L_d^p = L_d^p(\Omega,\mathcal,\mathbb) in d-dimensions, then we can define acceptance sets as below. Scalar Case An acceptance set is a set A satisfying: # A \supseteq L^p_+ # A \cap L^p_ = \emptyset such that L^p_ = \ # A \cap L^p_- = \ # Additionally if A is convex then it is a convex acceptance set ## And if A is a positively homogeneous cone then it is a coherent acceptance set Set-valued Case An acceptance set (in a space with d assets) is a set A \subseteq L^p_d satisfying: # u \in K_M \Rightarrow u1 \in A with 1 denoting the random variable that is constantly 1 \mathbb-a.s. # u \in -\mathrmK_M \Rightarrow u1 \not\in A # A is directionally closed in M with A + u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Financial Mathematics
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the Finance#Quantitative_finance, financial field. In general, there exist two separate branches of finance that require advanced quantitative techniques: Derivative (finance), derivatives pricing on the one hand, and risk management, risk and Investment management#Investment managers and portfolio structures, portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often with the help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when investment ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Convex Cone
In linear algebra, a cone—sometimes called a linear cone to distinguish it from other sorts of cones—is a subset of a real vector space that is closed under positive scalar multiplication; that is, C is a cone if x\in C implies sx\in C for every . This is a broad generalization of the standard cone in Euclidean space. A convex cone is a cone that is also closed under addition, or, equivalently, a subset of a vector space that is closed under linear combinations with positive coefficients. It follows that convex cones are convex sets. The definition of a convex cone makes sense in a vector space over any ordered field, although the field of real numbers is used most often. Definition A subset C of a vector space is a cone if x\in C implies sx\in C for every s>0. Here s>0 refers to (strict) positivity in the scalar field. Competing definitions Some other authors require ,\infty)C\subset C or even 0\in C. Some require a cone to be convex and/or satisfy C\cap-C\subset\. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Utility
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings. * In a normative context, utility refers to a goal or objective that we wish to maximize, i.e., an objective function. This kind of utility bears a closer resemblance to the original utilitarian concept, developed by moral philosophers such as Jeremy Bentham and John Stuart Mill. * In a descriptive context, the term refers to an ''apparent'' objective function; such a function is revealed by a person's behavior, and specifically by their preferences over lotteries, which can be any quantified choice. The relationship between these two kinds of utility functions has been a source of controversy among both economists and ethicists, with most maintaining that the two are distinct but generally related. Utility function Consider a set of alternatives among which a person has a preference ordering. A utility fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Entropic Risk Measure
In financial mathematics (concerned with mathematical modeling of financial markets), the entropic risk measure is a risk measure which depends on the risk aversion of the user through the exponential utility function. It is a possible alternative to other risk measures as value-at-risk or expected shortfall. It is a theoretically interesting measure because it provides different risk values for different individuals whose attitudes toward risk may differ. However, in practice it would be difficult to use since quantifying the risk aversion for an individual is difficult to do. The entropic risk measure is the prime example of a convex risk measure which is not coherent. Given the connection to utility functions, it can be used in utility maximization problems. Mathematical definition The entropic risk measure with the risk aversion parameter \theta > 0 is defined as : \rho^(X) = \frac\log\left(\mathbb ^right) = \sup_ \left\ \, where H(Q, P) = E\left frac\log\frac\right/math> ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Self-financing Portfolio
In financial mathematics, a self-financing portfolio is a portfolio having the feature that, if there is no exogenous infusion or withdrawal of money, the purchase of a new asset must be financed by the sale of an old one. This concept is used to define for example admissible strategies and replicating portfolios, the latter being fundamental for arbitrage-free derivative pricing. Mathematical definition Discrete time Assume we are given a discrete filtered probability space (\Omega,\mathcal,\_^T,P), and let K_t be the solvency cone (with or without transaction costs) at time ''t'' for the market. Denote by L_d^p(K_t) = \. Then a portfolio (H_t)_^T (in physical units, i.e. the number of each stock) is self-financing (with trading on a finite set of times only) if : for all t \in \ we have that H_t - H_ \in -K_t \; P-a.s. with the convention that H_ = 0. If we are only concerned with the set that the portfolio can be at some future time then we can say that H_ \in -K_0 - ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Superhedging Price
The superhedging price is a coherent risk measure. The superhedging price of a portfolio (A) is equivalent to the smallest amount necessary to be paid for an admissible portfolio (B) at the current time so that at some specified future time the value of B is at least as great as A. In a complete market the superhedging price is equivalent to the price for hedging the initial portfolio. Mathematical definition If the set of equivalent martingale measures is denoted by EMM then the superhedging price of a portfolio ''X'' is \rho(-X) where \rho is defined by : \rho(X) = \sup_ \mathbb^Q X/math>. \rho defined as above is a coherent risk measure. Acceptance set The acceptance set for the superhedging price is the negative of the set of values of a self-financing portfolio at the terminal time. That is : A = \. Subhedging price The subhedging price is the greatest value that can be paid so that in any possible situation at the specified future time you have a second portfolio worth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
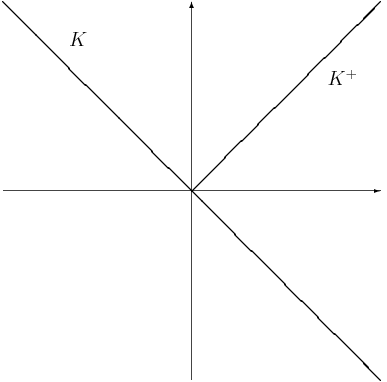
Solvency Cone
The solvency cone is a concept used in financial mathematics which models the possible trades in the financial market. This is of particular interest to markets with transaction costs. Specifically, it is the convex cone of portfolios that can be exchanged to portfolios of non-negative components (including paying of any transaction costs). Mathematical basis If given a bid-ask matrix \Pi for d assets such that \Pi = \left(\pi^\right)_ and m \leq d is the number of assets which with any non-negative quantity of them can be "discarded" (traditionally m = d), then the solvency cone K(\Pi) \subset \mathbb^d is the convex cone spanned by the unit vectors e^i, 1 \leq i \leq m and the vectors \pi^e^i-e^j, 1 \leq i,j \leq d. Definition A solvency cone K is any closed convex cone such that K \subseteq \mathbb^d and K \supseteq \mathbb^d_+. Uses A process of (random) solvency cones \left\_^T is a model of a financial market. This is sometimes called a market process. The negative of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Financial Regulation
Financial regulation is a broad set of policies that apply to the financial sector in most jurisdictions, justified by two main features of finance: systemic risk, which implies that the failure of financial firms involves public interest considerations; and information asymmetry, which justifies curbs on freedom of contract in selected areas of financial services, particularly those that involve retail clients and/or principal–agent problems. An integral part of financial regulation is the supervision of designated financial firms and markets by specialized authorities such as securities commissions and bank supervision, bank supervisors. In some jurisdictions, certain aspects of financial supervision are delegated to self-regulatory organizations. Financial regulation forms one of three legal categories which constitutes the content of financial law, the other two being market practices and case law. History In the early modern period, the Dutch were the pioneers in finan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Almost Surely
In probability theory, an event is said to happen almost surely (sometimes abbreviated as a.s.) if it happens with probability 1 (with respect to the probability measure). In other words, the set of outcomes on which the event does not occur has probability 0, even though the set might not be empty. The concept is analogous to the concept of "almost everywhere" in measure theory. In probability experiments on a finite sample space with a non-zero probability for each outcome, there is no difference between ''almost surely'' and ''surely'' (since having a probability of 1 entails including all the sample points); however, this distinction becomes important when the sample space is an infinite set, because an infinite set can have non-empty subsets of probability 0. Some examples of the use of this concept include the strong and uniform versions of the law of large numbers, the continuity of the paths of Brownian motion, and the infinite monkey theorem. The terms almost certai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Coherent Risk Measure
In the fields of actuarial science and financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a function that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance. Properties Consider a random outcome X viewed as an element of a linear space \mathcal of measurable functions, defined on an appropriate probability space. A functional \varrho : \mathcal → \R \cup \ is said to be coherent risk measure for \mathcal if it satisfies the following properties: Normalized : \varrho(0) = 0 That is, the risk when holding no assets is zero. Monotonicity : \mathrm\; Z_1,Z_2 \in \mathcal \;\mathrm\; Z_1 \leq Z_2 \; \mathrm ,\; \mathrm \; \varrho(Z_1) \geq \varrho(Z_2) That is, if portfolio Z_2 always has better values than portfolio Z_1 under almost all scenarios then the risk of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |