|
Axiom Of Elementary Sets
Zermelo set theory (sometimes denoted by Z-), as set out in a seminal paper in 1908 by Ernst Zermelo, is the ancestor of modern Zermelo–Fraenkel set theory (ZF) and its extensions, such as von Neumann–Bernays–Gödel set theory (NBG). It bears certain differences from its descendants, which are not always understood, and are frequently misquoted. This article sets out the original axioms, with the original text (translated into English) and original numbering. The axioms of Zermelo set theory The axioms of Zermelo set theory are stated for objects, some of which (but not necessarily all) are sets, and the remaining objects are urelements and not sets. Zermelo's language implicitly includes a membership relation ∈, an equality relation = (if it is not included in the underlying logic), and a unary predicate saying whether an object is a set. Later versions of set theory often assume that all objects are sets so there are no urelements and there is no need for the unary p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ernst Zermelo
Ernst Friedrich Ferdinand Zermelo (, ; 27 July 187121 May 1953) was a German logician and mathematician, whose work has major implications for the foundations of mathematics. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem. Furthermore, his 1929 work on ranking chess players is the first description of a model for pairwise comparison that continues to have a profound impact on various applied fields utilizing this method. Life Ernst Zermelo graduated from Berlin's Luisenstädtisches Gymnasium (now ) in 1889. He then studied mathematics, physics and philosophy at the University of Berlin, the University of Halle, and the University of Freiburg. He finished his doctorate in 1894 at the University of Berlin, awarded for a dissertation on the calculus of variations (''Untersuchungen zur Variationsrechnung''). Zermelo remained at the University of Berlin, where he was appointed assistant to Planck, under whose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abraham Fraenkel
Abraham Fraenkel ( he, אברהם הלוי (אדולף) פרנקל; February 17, 1891 – October 15, 1965) was a German-born Israeli mathematician. He was an early Zionist and the first Dean of Mathematics at the Hebrew University of Jerusalem. He is known for his contributions to axiomatic set theory, especially his additions to Ernst Zermelo's axioms, which resulted in the Zermelo–Fraenkel set theory. Biography Abraham Adolf Halevi Fraenkel studied mathematics at the Universities of Munich, Berlin, Marburg and Breslau. After graduating, he lectured at the University of Marburg from 1916, and was promoted to professor in 1922. In 1919 he married Wilhelmina Malka A. Prins (1892–1983). Due to the severe housing shortage in post-war Germany, for a few years the couple lived as subtenants at professor Hensel's place. After leaving Marburg in 1928, Fraenkel taught at the University of Kiel for a year. He then made the fateful choice of accepting a position at the Hebrew Un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number Object
In category theory, a natural numbers object (NNO) is an object endowed with a recursive structure similar to natural numbers. More precisely, in a category E with a terminal object 1, an NNO ''N'' is given by: # a global element ''z'' : 1 → ''N'', and # an arrow ''s'' : ''N'' → ''N'', such that for any object ''A'' of E, global element ''q'' : 1 → ''A'', and arrow ''f'' : ''A'' → ''A'', there exists a unique arrow ''u'' : ''N'' → ''A'' such that: # ''u'' ∘ ''z'' = ''q'', and # ''u'' ∘ ''s'' = ''f'' ∘ ''u''. In other words, the triangle and square in the following diagram commute. The pair (''q'', ''f'') is sometimes called the ''recursion data'' for ''u'', given in the form of a recursive definition: # ⊢ ''u'' (''z'') = ''q'' # ''y'' ∈E ''N'' ⊢ ''u'' (''s'' ''y'') = ''f'' (''u'' (''y'')) The above definition is the universal property of NNOs, meaning they are defined up to canonical isomorphism. If the arrow ''u'' as defined above merely has to exist, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topos Theory
In mathematics, a topos (, ; plural topoi or , or toposes) is a category that behaves like the category of sheaves of sets on a topological space (or more generally: on a site). Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic. The mathematical field that studies topoi is called topos theory. Grothendieck topos (topos in geometry) Since the introduction of sheaves into mathematics in the 1940s, a major theme has been to study a space by studying sheaves on a space. This idea was expounded by Alexander Grothendieck by introducing the notion of a "topos". The main utility of this notion is in the abundance of situations in mathematics where topological heuristics are very effective, but an honest topological space is lacking; it is sometimes possible to find a topos formaliz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinal Number
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals (first, second, th, etc.) aimed to extend enumeration to infinite sets. A finite set can be enumerated by successively labeling each element with the least natural number that has not been previously used. To extend this process to various infinite sets, ordinal numbers are defined more generally as linearly ordered labels that include the natural numbers and have the property that every set of ordinals has a least element (this is needed for giving a meaning to "the least unused element"). This more general definition allows us to define an ordinal number \omega that is greater than every natural number, along with ordinal numbers \omega + 1, \omega + 2, etc., which are even greater than \omega. A linear order such that every subset has a least element is called a well-order. The axiom of choice implies that every set can be well-ordered, and given two well-ordered sets, one is isomorphic to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom Of Infinity
In axiomatic set theory and the branches of mathematics and philosophy that use it, the axiom of infinity is one of the axioms of Zermelo–Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural numbers. It was first published by Ernst Zermelo as part of his set theory in 1908.Zermelo: ''Untersuchungen über die Grundlagen der Mengenlehre'', 1907, in: Mathematische Annalen 65 (1908), 261-281; Axiom des Unendlichen p. 266f. Formal statement In the formal language of the Zermelo–Fraenkel axioms, the axiom reads: :\exists \mathbf \, ( \empty \in \mathbf \, \land \, \forall x \in \mathbf \, ( \, ( x \cup \ ) \in \mathbf ) ) . In words, there is a set I (the set which is postulated to be infinite), such that the empty set is in I, and such that whenever any ''x'' is a member of I, the set formed by taking the union of ''x'' with its singleton is also a member of I. Such a set is sometimes called an inductive set. Inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gödel's Completeness Theorem
Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic. The completeness theorem applies to any first-order theory: If ''T'' is such a theory, and φ is a sentence (in the same language) and every model of ''T'' is a model of φ, then there is a (first-order) proof of φ using the statements of ''T'' as axioms. One sometimes says this as "anything universally true is provable". This does not contradict Gödel's incompleteness theorem, which shows that some formula φu is unprovable although true in the natural numbers, which are a particular model of a first-order theory describing them — φu is just false in some other model of the first-order theory being considered (such as a non-standard model of arithmetic for Peano arithmetic). It makes a close link between model theory that deals with what is true in different models, and proof theory tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
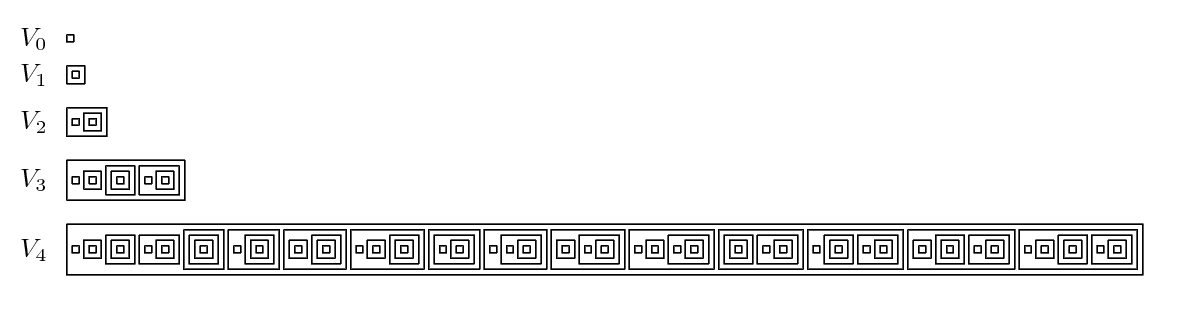
Von Neumann Universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930. The rank of a well-founded set is defined inductively as the smallest ordinal number greater than the ranks of all members of the set. In particular, the rank of the empty set is zero, and every ordinal has a rank equal to itself. The sets in ''V'' are divided into the transfinite hierarchy ''Vα'', called the cumulative hierarchy, based on their rank. Definition The cumulative hierarchy is a collection of sets ''V''α indexed by the class of ordinal numbers; in particular, ''V''α is the set of all sets having ranks less than α. Thus there is one set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second-order Logic
In logic and mathematics, second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory. First-order logic quantifies only variables that range over individuals (elements of the domain of discourse); second-order logic, in addition, also quantifies over relations. For example, the second-order sentence \forall P\,\forall x (Px \lor \neg Px) says that for every formula ''P'', and every individual ''x'', either ''Px'' is true or not(''Px'') is true (this is the law of excluded middle). Second-order logic also includes quantification over sets, functions, and other variables (see section below). Both first-order and second-order logic use the idea of a domain of discourse (often called simply the "domain" or the "universe"). The domain is a set over which individual elements may be quantified. Examples First-order logic can quantify over individuals, bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom Schema
In mathematical logic, an axiom schema (plural: axiom schemata or axiom schemas) generalizes the notion of axiom. Formal definition An axiom schema is a formula in the metalanguage of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which may or may not be required to satisfy certain conditions. Often, such conditions require that certain variables be free, or that certain variables not appear in the subformula or term. Finite axiomatization Given that the number of possible subformulas or terms that can be inserted in place of a schematic variable is countably infinite, an axiom schema stands for a countably infinite set of axioms. This set can usually be defined recursively. A theory that can be axiomatized without schemata is said to be finitely axiomatized. Theories that can be finitely axiomatized are seen as a bit more metamathematically elegant, even if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-formed Formula
In mathematical logic, propositional logic and predicate logic, a well-formed formula, abbreviated WFF or wff, often simply formula, is a finite sequence of symbols from a given alphabet that is part of a formal language. A formal language can be identified with the set of formulas in the language. A formula is a syntactic object that can be given a semantic meaning by means of an interpretation. Two key uses of formulas are in propositional logic and predicate logic. Introduction A key use of formulas is in propositional logic and predicate logic such as first-order logic. In those contexts, a formula is a string of symbols φ for which it makes sense to ask "is φ true?", once any free variables in φ have been instantiated. In formal logic, proofs can be represented by sequences of formulas with certain properties, and the final formula in the sequence is what is proven. Although the term "formula" may be used for written marks (for instance, on a piece of paper or ch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Neumann Ordinal
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals (first, second, th, etc.) aimed to extend enumeration to infinite sets. A finite set can be enumerated by successively labeling each element with the least natural number that has not been previously used. To extend this process to various infinite sets, ordinal numbers are defined more generally as linearly ordered labels that include the natural numbers and have the property that every set of ordinals has a least element (this is needed for giving a meaning to "the least unused element"). This more general definition allows us to define an ordinal number \omega that is greater than every natural number, along with ordinal numbers \omega + 1, \omega + 2, etc., which are even greater than \omega. A linear order such that every subset has a least element is called a well-order. The axiom of choice implies that every set can be well-ordered, and given two well-ordered sets, one is isomorphic to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |