|
Auto-correlation
Autocorrelation, sometimes known as serial correlation in the discrete time case, measures the correlation of a signal with a delayed copy of itself. Essentially, it quantifies the similarity between observations of a random variable at different points in time. The analysis of autocorrelation is a mathematical tool for identifying repeating patterns or hidden periodicities within a signal obscured by noise. Autocorrelation is widely used in signal processing, time domain and time series analysis to understand the behavior of data over time. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Various time series models incorporate autocorrelation, such as unit root processes, trend-stationary processes, autoregressive processes, and moving average processes. Autocorrelation of stochastic processes In statistics, the autocorrelation of a real or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series Analysis
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''forec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autocovariance
In probability theory and statistics, given a stochastic process, the autocovariance is a function that gives the covariance of the process with itself at pairs of time points. Autocovariance is closely related to the autocorrelation of the process in question. Auto-covariance of stochastic processes Definition With the usual notation \operatorname for the expectation operator, if the stochastic process \left\ has the mean function \mu_t = \operatorname _t/math>, then the autocovariance is given by where t_1 and t_2 are two instances in time. Definition for weakly stationary process If \left\ is a weakly stationary (WSS) process, then the following are true: :\mu_ = \mu_ \triangleq \mu for all t_1,t_2 and :\operatorname X_t, ^2, with 1 indicating perfect correlation and −1 indicating perfect anti-correlation. For a WSS process, the definition is :\rho_(\tau) = \frac = \frac. where :\operatorname_(0) = \sigma^2. Properties Symmetry property :\operatorname_(t_1,t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acf New
ACF or acf may refer to: Organizations Asia * Adivasi Cobra Force, extremist Santal organisation in Assam * Arab Chess Federation * Asian Chess Federation Australia * Australian Cat Federation, a standards organization for cat breeds * Australian Chess Federation, the governing body for chess in Australia * Australian Conservation Foundation, an Australian non-profit promoting ecological sustainability Europe * Action contre la Faim or Action Against Hunger, global humanitarian organization * ACF Fiorentina, Associazione Calcio Fiorentina, Italian football club * Army Cadet Force, British youth organisation that offers progressive military training to boys and girls aged 12 to 18 * Ateliers et Chantiers de France, defunct French shipyard * Automobile Club of France, men's club located on Place de la Concorde in Paris North America * Academic Competition Federation, an unincorporated non-profit organization that runs collegiate quizbowl tournaments * Administration for Chil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The nami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a relative change in the other quantity proportional to the change raised to a constant exponent: one quantity varies as a power of another. The change is independent of the initial size of those quantities. For instance, the area of a square has a power law relationship with the length of its side, since if the length is doubled, the area is multiplied by 2, while if the length is tripled, the area is multiplied by 3, and so on. Empirical examples The distributions of a wide variety of physical, biological, and human-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, cloud sizes, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well Defined
In mathematics, a well-defined expression or unambiguous expression is an expression whose definition assigns it a unique interpretation or value. Otherwise, the expression is said to be ''not well defined'', ill defined or ''ambiguous''. A function is well defined if it gives the same result when the representation of the input is changed without changing the value of the input. For instance, if f takes real numbers as input, and if f(0.5) does not equal f(1/2) then f is not well defined (and thus not a function). The term ''well-defined'' can also be used to indicate that a logical expression is unambiguous or uncontradictory. A function that is not well defined is not the same as a function that is undefined. For example, if f(x)=\frac, then even though f(0) is undefined, this does not mean that the function is ''not'' well defined; rather, 0 is not in the domain of f. Example Let A_0,A_1 be sets, let A = A_0 \cup A_1 and "define" f: A \rightarrow \ as f(a)=0 if a \in A_0 an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Conjugation
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - bi. The complex conjugate of z is often denoted as \overline or z^*. In polar form, if r and \varphi are real numbers then the conjugate of r e^ is r e^. This can be shown using Euler's formula. The product of a complex number and its conjugate is a real number: a^2 + b^2 (or r^2 in polar coordinates). If a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. Notation The complex conjugate of a complex number z is written as \overline z or z^*. The first notation, a vinculum, avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of the complex conjugate. The second is preferred in physics, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
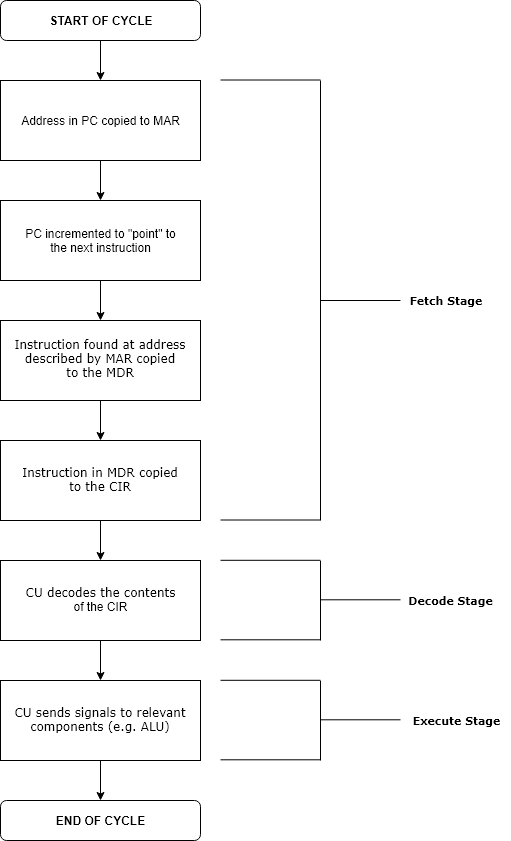
Execution (computing)
Execution in computer and software engineering is the process by which a computer or virtual machine interprets and acts on the instructions of a computer program. Each instruction of a program is a description of a particular action which must be carried out, in order for a specific problem to be solved. Execution involves repeatedly following a " fetch–decode–execute" cycle for each instruction done by the control unit. As the executing machine follows the instructions, specific effects are produced in accordance with the semantics of those instructions. Programs for a computer may be executed in a batch process without human interaction or a user may type commands in an interactive session of an interpreter. In this case, the "commands" are simply program instructions, whose execution is chained together. The term run is used almost synonymously. A related meaning of both "to run" and "to execute" refers to the specific action of a user starting (or ''launching'' or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Realization (probability)
In probability and statistics, a realization, observation, or observed value, of a random variable is the value that is actually observed (what actually happened). The random variable itself is the process dictating how the observation comes about. Statistical quantities computed from realizations without deploying a statistical model are often called "empirical", as in empirical distribution function or empirical probability. Conventionally, to avoid confusion, upper case letters denote random variables; the corresponding lower case letters denote their realizations. Formal definition In more formal probability theory, a random variable is a function ''X'' defined from a sample space Ω to a measurable space called the state space. If an element in Ω is mapped to an element in state space by ''X'', then that element in state space is a realization. Elements of the sample space can be thought of as all the different possibilities that ''could'' happen; while a re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |