|
Anhemitonia
Musicology commonly classifies scales as either hemitonic or anhemitonic. Hemitonic scales contain one or more semitones, while anhemitonic scales do not contain semitones. For example, in traditional Japanese music, the anhemitonic ''yo'' scale is contrasted with the hemitonic ''in'' scale. The simplest and most commonly used scale in the world is the atritonic anhemitonic "major" pentatonic scale. The whole tone scale is also anhemitonic. A special subclass of the hemitonic scales is the cohemitonic scales. Cohemitonic scales contain two or more semitones (making them hemitonic) such that two or more of the semitones appear consecutively in scale order. For example, the Hungarian minor scale in C includes F, G, and A in that order, with a semitone between F and G, and then a semitone between G and A. Ancohemitonic scales, in contrast, either contain no semitones (and thus are anhemitonic), or contain semitones (being hemitonic) where none of the semitones appear conse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musicology
Musicology (from Greek μουσική ''mousikē'' 'music' and -λογια ''-logia'', 'domain of study') is the scholarly analysis and research-based study of music. Musicology departments traditionally belong to the humanities, although some music research is scientific in focus (psychological, sociological, acoustical, neurological, computational). Some geographers and anthropologists have an interest in musicology so the social sciences also have an academic interest. A scholar who participates in musical research is a musicologist. Musicology traditionally is divided in three main branches: historical musicology, systematic musicology and ethnomusicology. Historical musicologists mostly study the history of the western classical music tradition, though the study of music history need not be limited to that. Ethnomusicologists draw from anthropology (particularly field research) to understand how and why people make music. Systematic musicology includes music theory, aesthe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
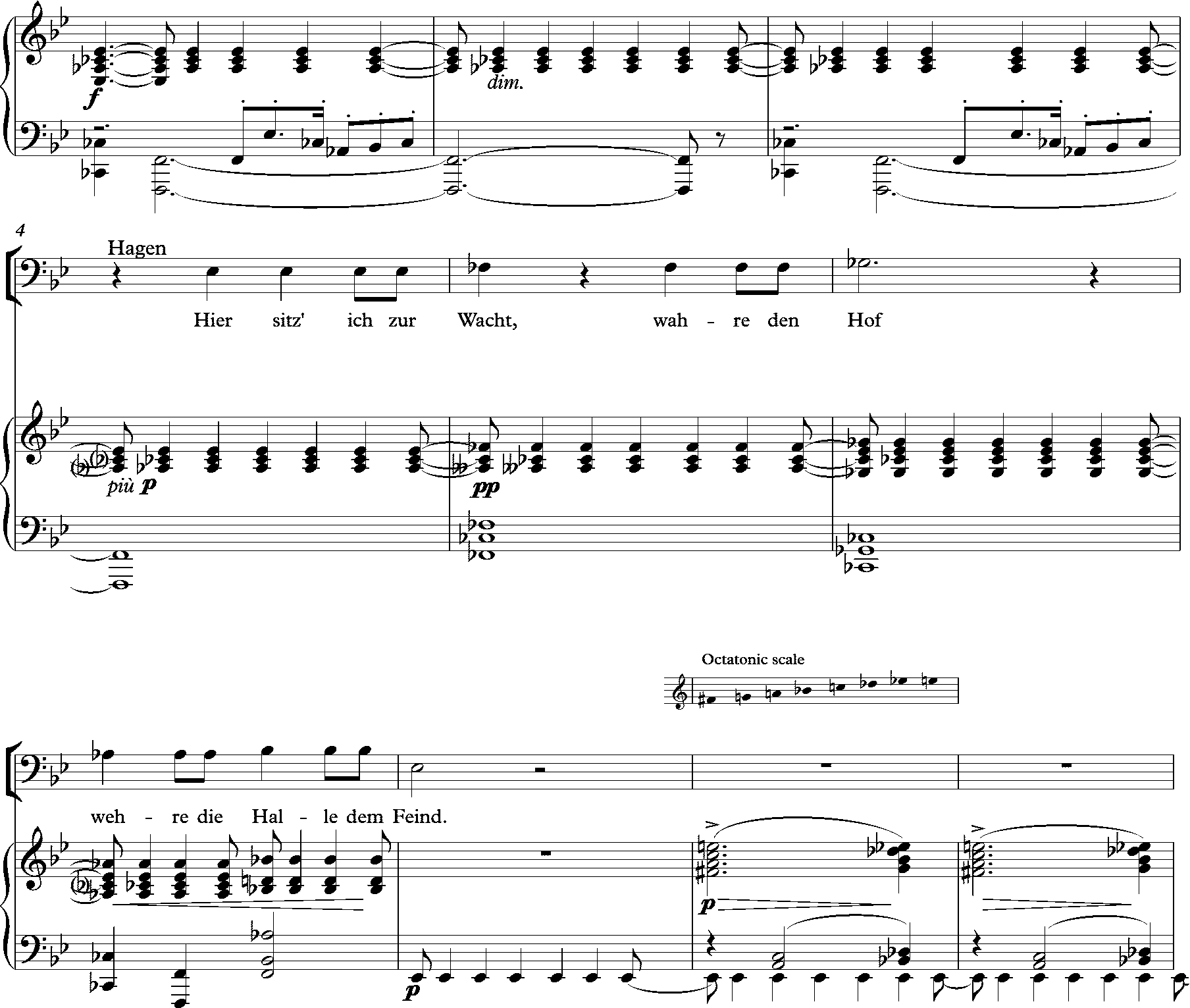
Octatonic Scale
An octatonic scale is any eight-note musical scale. However, the term most often refers to the symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory (in contrast to jazz theory), this symmetrical scale is commonly called the ''octatonic scale'' (or the ''octatonic collection''), although there are a total of 42 enharmonically non-equivalent, transpositionally non-equivalent eight-note sets. The earliest systematic treatment of the octatonic scale was in Edmond de Polignac's unpublished treatise "Étude sur les successions alternantes de tons et demi-tons (Et sur la gamme dite majeure-mineure)" (''Study of the Succession of Alternating Whole Tones and Semitones (and of the so-called Major-Minor Scale)'') from c. 1879, which preceded Vito Frazzi's ''Scale alternate per pianoforte'' of 1930 by a full half-century. Nomenclature In Saint Petersburg at the turn of the 20th century, this scale had become so familiar in the circle of comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resolution (music)
Resolution in western tonal music theory is the move of a note or chord from dissonance (an unstable sound) to a consonance (a more final or stable sounding one). Dissonance, resolution, and suspense can be used to create musical interest. Where a melody or chordal pattern is expected to resolve to a certain note or chord, a different but similarly suitable note can be resolved to instead, creating an interesting and unexpected sound. For example, the deceptive cadence. Basis Resolution has a strong basis in tonal music, since atonal music generally contains a more constant level of dissonance and lacks a tonal center to which to resolve. The concept of "resolution", and the degree to which resolution is "expected", is contextual as to culture and historical period. In a classical piece of the Baroque period, for example, an added sixth chord (made up of the notes C, E, G and A, for example) has a very strong need to resolve, while in a more modern work, that need is less ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leading Tone
In music theory, a leading-tone (also called a subsemitone, and a leading-note in the UK) is a note or pitch which resolves or "leads" to a note one semitone higher or lower, being a lower and upper leading-tone, respectively. Typically, ''the'' leading tone refers to the seventh scale degree of a major scale (), a major seventh above the tonic. In the movable do solfège system, the leading-tone is sung as ''ti''. A leading-tone triad is a triad built on the seventh scale degree in a major key (vii in Roman numeral analysis), while a leading-tone seventh chord is a seventh chord built on the seventh scale degree (vii7). Walter Piston considers and notates vii as V, an incomplete dominant seventh chord. (For the Roman numeral notation of these chords, see Roman numeral analysis.) Note Seventh scale degree (or lower leading tone) Typically, when people speak of ''the'' leading tone, they mean the seventh scale degree () of the major scale, which has a strong affinity for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tonic (music)
In music, the tonic is the first scale degree () of the diatonic scale (the first note of a scale) and the tonal center or final resolution tone that is commonly used in the final cadence in tonal (musical key-based) classical music, popular music, and traditional music. In the movable do solfège system, the tonic note is sung as ''do''. More generally, the tonic is the note upon which all other notes of a piece are hierarchically referenced. Scales are named after their tonics: for instance, the tonic of the C major scale is the note C. The triad formed on the tonic note, the tonic chord, is thus the most significant chord in these styles of music. In Roman numeral analysis, the tonic chord is typically symbolized by the Roman numeral "I" if it is major and by "i" if it is minor. These chords may also appear as seventh chords: in major, as IM7, or in minor as i7 or rarely iM7: The tonic is distinguished from the root, which is the reference note of a chord, rathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Vector
In musical set theory, an interval vector is an array of natural numbers which summarize the intervals present in a set of pitch classes. (That is, a set of pitches where octaves are disregarded.) Other names include: ic vector (or interval-class vector), PIC vector (or pitch-class interval vector) and APIC vector (or absolute pitch-class interval vector, which Michiel Schuijer states is more proper.) While primarily an analytic tool, interval vectors can also be useful for composers, as they quickly show the sound qualities that are created by different collections of pitch class. That is, sets with high concentrations of conventionally dissonant intervals (i.e., seconds and sevenths) sound more dissonant, while sets with higher numbers of conventionally consonant intervals (i.e., thirds and sixths) sound more consonant. While the actual perception of consonance and dissonance involves many contextual factors, such as register, an interval vector can nevertheless be a help ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Vector
In musical set theory, an interval vector is an array of natural numbers which summarize the intervals present in a set of pitch classes. (That is, a set of pitches where octaves are disregarded.) Other names include: ic vector (or interval-class vector), PIC vector (or pitch-class interval vector) and APIC vector (or absolute pitch-class interval vector, which Michiel Schuijer states is more proper.) While primarily an analytic tool, interval vectors can also be useful for composers, as they quickly show the sound qualities that are created by different collections of pitch class. That is, sets with high concentrations of conventionally dissonant intervals (i.e., seconds and sevenths) sound more dissonant, while sets with higher numbers of conventionally consonant intervals (i.e., thirds and sixths) sound more consonant. While the actual perception of consonance and dissonance involves many contextual factors, such as register, an interval vector can nevertheless be a help ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Pentatonic Scale
A pentatonic scale is a musical scale with five notes per octave, in contrast to the heptatonic scale, which has seven notes per octave (such as the major scale and minor scale). Pentatonic scales were developed independently by many ancient civilizations and are still used in various musical styles to this day. There are two types of pentatonic scales: those with semitones (hemitonic) and those without (anhemitonic). Types Hemitonic and anhemitonic Musicology commonly classifies pentatonic scales as either ''hemitonic'' or ''anhemitonic''. Hemitonic scales contain one or more semitones and anhemitonic scales do not contain semitones. (For example, in Japanese music the anhemitonic ''yo'' scale is contrasted with the hemitonic ''in'' scale.) Hemitonic pentatonic scales are also called "ditonic scales", because the largest interval in them is the ditone (e.g., in the scale C–E–F–G–B–C, the interval found between C–E and G–B). (This should not be con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music," the use of which is "common in most musical systems." The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' ( it, all'ottava), ''8va bassa'' ( it, all'ottava bassa, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by placing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Of Fifths
In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths. (This is strictly true in the standard 12-tone equal temperament system — using a different system requires one interval of diminished sixth to be treated as a fifth). If C is chosen as a starting point, the sequence is: C, G, D, A, E, B (=C), F (=G), C (=D), A, E, B, F. Continuing the pattern from F returns the sequence to its starting point of C. This order places the most closely related key signatures adjacent to one another. It is usually illustrated in the form of a circle. Definition The circle of fifths organizes pitches in a sequence of perfect fifths, generally shown as a circle with the pitches (and their corresponding keys) in a clockwise progression. Musicians and composers often use the circle of fifths to describe the musical relationships between pitches. Its design is helpful in composing and harmonizing melodies, building chords, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octatonic Scale
An octatonic scale is any eight-note musical scale. However, the term most often refers to the symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory (in contrast to jazz theory), this symmetrical scale is commonly called the ''octatonic scale'' (or the ''octatonic collection''), although there are a total of 42 enharmonically non-equivalent, transpositionally non-equivalent eight-note sets. The earliest systematic treatment of the octatonic scale was in Edmond de Polignac's unpublished treatise "Étude sur les successions alternantes de tons et demi-tons (Et sur la gamme dite majeure-mineure)" (''Study of the Succession of Alternating Whole Tones and Semitones (and of the so-called Major-Minor Scale)'') from c. 1879, which preceded Vito Frazzi's ''Scale alternate per pianoforte'' of 1930 by a full half-century. Nomenclature In Saint Petersburg at the turn of the 20th century, this scale had become so familiar in the circle of comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Scale
In music and music theory, a hexatonic scale is a scale with six pitches or notes per octave. Famous examples include the whole-tone scale, C D E F G A C; the augmented scale, C D E G A B C; the Prometheus scale, C D E F A B C; and the blues scale, C E F G G B C. A hexatonic scale can also be formed by stacking perfect fifths. This results in a diatonic scale with one note removed (for example, A C D E F G). Whole-tone scale The whole-tone scale is a series of whole tones. It has two non-enharmonically equivalent positions: C D E F G A C and D E F G A B D. It is primarily associated with the French impressionist composer Claude Debussy, who used it in such pieces of his as ''Voiles'' and ''Le vent dans la plaine'', both from his first book of piano '' Préludes''. This whole-tone scale has appeared occasionally and sporadically in jazz at least since Bix Beiderbecke's impressionistic piano piece ''In a Mist''. Bop pianist Thelonious Monk often interpolated whole-tone scale flo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
