|
Algebra II
In contemporary education, mathematics education, known in Europe as the didactics or pedagogy of mathematics – is the practice of teaching, learning and carrying out scholarly research into the transfer of mathematical knowledge. Although research into mathematics education is primarily concerned with the tools, methods and approaches that facilitate practice or the study of practice, it also covers an extensive field of study encompassing a variety of different concepts, theories and methods. National and international organisations regularly hold conferences and publish literature in order to improve mathematics education. History Ancient Elementary mathematics were a core part of education in many ancient civilisations, including ancient Egypt, ancient Babylonia, ancient Greece, ancient Rome and Vedic India. In most cases, formal education was only available to male children with sufficiently high status, wealth or caste. The oldest known mathematics textbook is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Lecture At The Helsinki University Of Technology
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Male
Male (symbol: ♂) is the sex of an organism that produces the gamete (sex cell) known as sperm, which fuses with the larger female gamete, or ovum, in the process of fertilization. A male organism cannot reproduce sexually without access to at least one ovum from a female, but some organisms can reproduce both sexually and asexually. Most male mammals, including male humans, have a Y chromosome, which codes for the production of larger amounts of testosterone to develop male reproductive organs. Not all species share a common sex-determination system. In most animals, including humans, sex is determined genetically; however, species such as ''Cymothoa exigua'' change sex depending on the number of females present in the vicinity. In humans, the word ''male'' can also be used to refer to gender in the social sense of gender role or gender identity. Overview The existence of separate sexes has evolved independently at different times and in different lineages, an example ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today. History The prehistory of arithmetic is limited to a small number of artifacts, which may indicate the conception of addition and subtraction, the best-known being the Ishango bone from central Africa, dating from somewhere between 20,000 and 18,000 BC, although its interpretation is disputed. The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations: addition, subtraction, multiplication, and division, as early as 2000 BC. These artifacts do not always reveal the specific process used for solving problems, but t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrivium
From the time of Plato through the Middle Ages, the ''quadrivium'' (plural: quadrivia) was a grouping of four subjects or arts—arithmetic, geometry, music, and astronomy—that formed a second curricular stage following preparatory work in the ''trivium'', consisting of grammar, logic, and rhetoric. Together, the '' trivium'' and the ''quadrivium'' comprised the seven liberal arts, and formed the basis of a liberal arts education in Western society until gradually displaced as a curricular structure by the ''studia humanitas'' and its later offshoots, beginning with Petrarch in the 14th century. The seven classical arts were considered "thinking skills" and were distinguished from practical arts, such as medicine and architecture. The ''quadrivium'', Latin for 'four ways', and its use for the four subjects have been attributed to Boethius—who likely coined the term. It was considered the foundation for the study of philosophy (sometimes called the "liberal art ''par excellen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trivium (education)
The trivium is the lower division of the seven liberal arts and comprises grammar, logic, and rhetoric. The trivium is implicit in ''De nuptiis Philologiae et Mercurii'' ("On the Marriage of Philology and Mercury") by Martianus Capella, but the term was not used until the Carolingian Renaissance, when it was coined in imitation of the earlier quadrivium. Grammar, logic, and rhetoric were essential to a classical education, as explained in Plato's dialogues. The three subjects together were denoted by the word ''trivium'' during the Middle Ages, but the tradition of first learning those three subjects was established in ancient Greece. Contemporary iterations have taken various forms, including those found in certain British and American universities (some being part of the Classical education movement) and at the independent Oundle School in the United Kingdom. Etymology Etymologically, the Latin word trivium means "the place where three roads meet" (tri + via); hence, the subje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liberal Arts
Liberal arts education (from Latin "free" and "art or principled practice") is the traditional academic course in Western higher education. ''Liberal arts'' takes the term ''art'' in the sense of a learned skill rather than specifically the fine arts. ''Liberal arts education'' can refer to studies in a liberal arts degree course or to a university education more generally. Such a course of study contrasts with those that are principally vocational, professional, or technical. History Before they became known by their Latin variations (, , ), the liberal arts were the continuation of Ancient Greek methods of enquiry that began with a "desire for a universal understanding." Pythagoras argued that there was a mathematical and geometrical harmony to the cosmos or the universe; his followers linked the four arts of astronomy, mathematics, geometry, and music into one area of study to form the "disciplines of the mediaeval quadrivium". In 4th-century B.C.E. Athens, the governmen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plato
Plato ( ; grc-gre, Πλάτων ; 428/427 or 424/423 – 348/347 BC) was a Greek philosopher born in Athens during the Classical period in Ancient Greece. He founded the Platonist school of thought and the Academy, the first institution of higher learning on the European continent. Along with his teacher, Socrates, and his student, Aristotle, Plato is a central figure in the history of Ancient Greek philosophy and the Western and Middle Eastern philosophies descended from it. He has also shaped religion and spirituality. The so-called neoplatonism of his interpreter Plotinus greatly influenced both Christianity (through Church Fathers such as Augustine) and Islamic philosophy (through e.g. Al-Farabi). In modern times, Friedrich Nietzsche diagnosed Western culture as growing in the shadow of Plato (famously calling Christianity "Platonism for the masses"), while Alfred North Whitehead famously said: "the safest general characterization of the European philosophical tra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
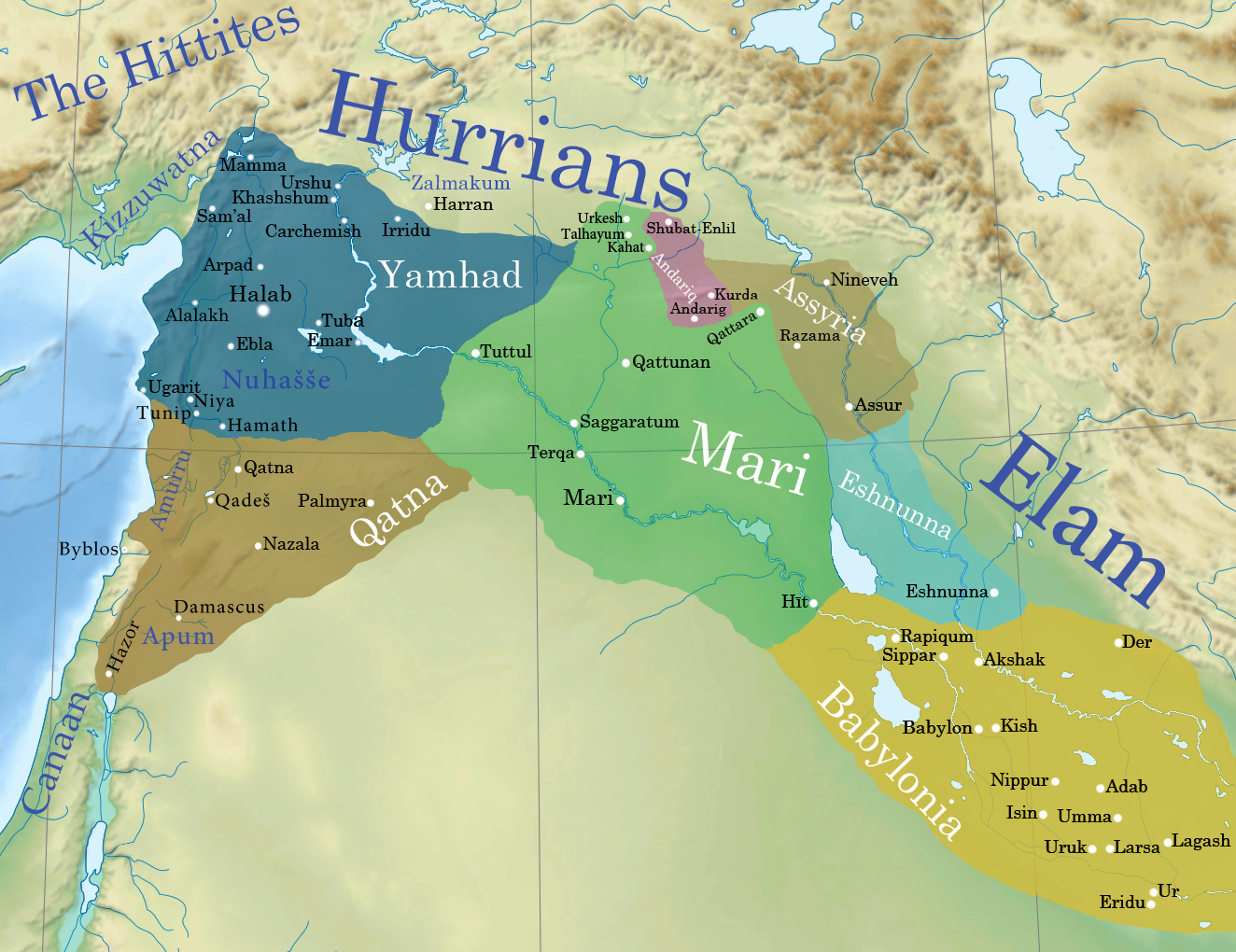
Eshnunna
Eshnunna (modern Tell Asmar in Diyala Governorate, Iraq) was an ancient Sumerian (and later Akkadian) city and city-state in central Mesopotamia 12.6 miles northwest of Tell Agrab and 15 miles northwest of Tell Ishchali. Although situated in the Diyala Valley north-west of Sumer proper, the city nonetheless belonged securely within the Sumerian cultural milieu. It is sometimes, in archaeological papers, called Ashnunnak or Tuplias,. The tutelary deity of the city was Tishpak (Tišpak) (having replaced Ninazu) though other gods, including Sin, Adad, and Inanna of Kititum were also worshiped there. The personal goddess of the rulers were Belet-Šuḫnir and Belet-Terraban. History Early Bronze Inhabited since the Jemdet Nasr period, around 3000 BC, Eshnunna was a major city during the Early Dynastic period of Mesopotamia. It is known, from cuneiform records and excavations, that the city was occupied in the Akkadian period though its extent was noticeably less than it reache ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Db2-146
IM 67118, also known as Db2-146, is an Old Babylonian clay tablet in the collection of the National Museum of Iraq that contains the solution to a problem in plane geometry concerning a rectangle with given area and diagonal. In the last part of the text the solution is proved correct by means of the Pythagorean theorem. The steps of the solution are believed to represent cut-and-paste geometry operations involving a diagram from which, it has been suggested, ancient Mesopotamians might, at an earlier time, have derived the Pythagorean theorem. Description The tablet was excavated in 1962 at Tell edh-Dhiba'i, an Old Babylonian settlement near modern Baghdad that was once part of the kingdom of Eshnunna, and was published by Taha Baqir in the same year. It dates to approximately 1770 BCE (according to the middle chronology), during the reign of Ibal-pi-el II, who ruled Eshnunna at the same time that Hammurabi ruled Babylon. The tablet measures 11.5×6.8×3.3 cm. Its langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagoras
Pythagoras of Samos ( grc, Πυθαγόρας ὁ Σάμιος, Pythagóras ho Sámios, Pythagoras the Samos, Samian, or simply ; in Ionian Greek; ) was an ancient Ionians, Ionian Ancient Greek philosophy, Greek philosopher and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of Plato, Aristotle, and, through them, the Western philosophy, West in general. Knowledge of his life is clouded by legend, but he appears to have been the son of Mnesarchus, a gem-engraver on the island of Samos. Modern scholars disagree regarding Pythagoras's education and influences, but they do agree that, around 530 BC, he travelled to Crotone, Croton in southern Italy, where he founded a school in which initiates were sworn to secrecy and lived a communal, asceticism, ascetic lifestyle. This lifestyle entailed a number of dietary prohibitions, traditionally said to have included vegetarianism, although m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Old Babylonian Empire
The Old Babylonian Empire, or First Babylonian Empire, is dated to BC – BC, and comes after the end of Sumerian power with the destruction of the Third Dynasty of Ur, and the subsequent Isin-Larsa period. The chronology of the first dynasty of Babylonia is debated, since there is a Babylonian King List A and also a Babylonian King List B. In this chronology, the regnal years of List A are used due to their wide usage. The reign lengths given in List B are longer, generally speaking. Hardship of searching for origins of the First Dynasty The actual origins of the First Babylonian dynasty are rather hard to pinpoint with great certainty — simply because Babylon itself, due to a high water table, yields very few archaeological materials intact. Thus, the evidence that survived throughout the years includes written records such as royal and votive inscriptions, literary texts, and lists of year-names. The minimal amount of evidence in economic and legal documents makes it diff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides ''a'', ''b'' and the hypotenuse ''c'', often called the Pythagorean equation: :a^2 + b^2 = c^2 , The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |