|
Al-Khazini
Abū al-Fath Abd al-Rahman Mansūr al-Khāzini or simply al-Khāzini (, flourished 1115–1130) was an Iranian astronomer of Greek origin from Seljuk Persia. His astronomical tables written under the patronage of Sultan Sanjar (', 1115) is considered to be one of the major works in mathematical astronomy of the medieval period. Montelle, C. (2011). The ‘Well-Known Calendars’: Al-Khāzinī’s Description of Significant Chronological Systems for Medieval Mathematical Astronomy in Arabic. In Steele J. (Ed.), Calendars and Years II: Astronomy and Time in the Ancient and Medieval World (pp. 107-126). Oxford; Oakville: Oxbow Books. He provided the positions of fixed stars, and for oblique ascensions and time-equations for the latitude of Marv in which he was based.Meyerhof, M. (1948). 'Alī al-Bayhaqī's Tatimmat Siwān al-Hikma: A Biographical Work on Learned Men of the Islam. Osiris, 8, 122-217. He also wrote extensively on various calendrical systems and on the various manip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Muslims
Greek Muslims, also known as Grecophone Muslims, are Muslims of Greek ethnic origin whose adoption of Islam (and often the Turkish language and identity) dates to the period of Ottoman rule in the southern Balkans. They consist primarily of the descendants of the elite Ottoman Janissary corps and Ottoman-era converts to Islam from Greek Macedonia (e.g., Vallahades), Crete (Cretan Muslims), and northeastern Anatolia and the Pontic Alps (Pontic Greeks). They are currently found mainly in the west of Turkey (particularly the regions of Izmir, Bursa, and Edirne) and the northeast (particularly in the regions of Trabzon, Gümüşhane, Sivas, Erzincan, Erzurum, and Kars). Despite their ethnic Greek origin, the contemporary Grecophone Muslims of Turkey have been steadily assimilated into the Turkish-speaking Muslim population. Sizable numbers of Grecophone Muslims, not merely the elders but even young people, have retained knowledge of their respective Greek dialects, such as Cret ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Islamic Astronomy
Islamic astronomy comprises the Astronomy, astronomical developments made in the Islamic world, particularly during the Islamic Golden Age (9th–13th centuries), and mostly written in the Arabic language. These developments mostly took place in the Middle East, Central Asia, Al-Andalus, and North Africa, and later in the Far East and History of India, India. It closely parallels the genesis of other Islamic sciences in its assimilation of foreign material and the amalgamation of the disparate elements of that material to create a science with Islamic characteristics. These included Greek astronomy, Greek, Sassanid Empire, Sassanid, and Indian astronomy, Indian works in particular, which were translated and built upon. Islamic astronomy played a significant role in the revival of Byzantine science, Byzantine and Science in Medieval Western Europe, EuropeanSaliba (1999). astronomy following the Dark Ages (historiography), loss of knowledge during the early medieval period, notably ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Omar Khayyam
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīsābūrī (18 May 1048 – 4 December 1131), commonly known as Omar Khayyam ( fa, عمر خیّام), was a polymath, known for his contributions to mathematics, astronomy, philosophy, and Persian poetry. He was born in Nishapur, the initial capital of the Seljuk Empire. As a scholar, he was contemporary with the rule of the Seljuk dynasty around the time of the First Crusade. As a mathematician, he is most notable for his work on the classification and solution of cubic equations, where he provided geometric solutions by the intersection of conics. Khayyam also contributed to the understanding of the parallel axiom.Struik, D. (1958). "Omar Khayyam, mathematician". ''The Mathematics Teacher'', 51(4), 280–285. As an astronomer, he calculated the duration of the solar year with remarkable precision and accuracy, and designed the Jalali calendar, a solar calendar with a very precise 33-year intercalation cycle''The Cam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Al-Isfizari
Abū Ḥātim al-Muẓaffar al-Isfazārī (Floruit, fl. late 11th or early 12th century) was an Islamic mathematician, astronomer and engineer from Khurasan. According to the historian and geographer Ibn al-Athir and the polymath Qutb al-Din al-Shirazi, he worked in the Seljuq Empire, Seljuq observatory of Isfahan. The Persian writer Nezami Aruzi met him in Balkh in (in present‐day Afghanistan) in 1112 or 1113. He was a contemporary of Umar al-Khayyam and Al-Khazini, Abd al-Raḥmān al-Khāzinī. He main work is entitled ''Irshād dhawī al-cirfān ilā ṣinācat al-qaffān'' (Guiding the possessors of learning in the art of the steelyard), a relatively long text on the theory of the steelyard balance with unequal arms. His other surviving works include a summary of Euclid's Elements, a text on geometrical measurements, and a treatise on meteorology in Persian language. Al-Isfazārī's corpus of mechanics is composed of two sets of texts, which have been published in ''Matn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oneworld Publications
Oneworld Publications is a British independent publishing firm founded in 1986 by Novin Doostdar and Juliet Mabey originally to publish accessible non-fiction by experts and academics for the general market."About Us" Oneworld Publications. Based in , it later added a literary fiction list (in 2009) and both a children's list (Rock the Boat, 2015) and an upmarket crime list (Point Blank, 2016), and now publishes across a wide range of subjects, including history, politics, current affairs, popular science, religion, philosophy, and psychology, as well as literary fiction, crime fiction and suspense, and children's titles. A large proportion of Oneworld fiction across all its lists is translated. Among the writers on th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighing Scale
A scale or balance is a device used to measure weight or mass. These are also known as mass scales, weight scales, mass balances, and weight balances. The traditional scale consists of two plates or bowls suspended at equal distances from a fulcrum. One plate holds an object of unknown mass (or weight), while known masses are added to the other plate until static equilibrium is achieved and the plates level off, which happens when the masses on the two plates are equal. The perfect scale rests at neutral. A spring scale will make use of a spring of known stiffness to determine mass (or weight). Suspending a certain mass will extend the spring by a certain amount depending on the spring's stiffness (or spring constant). The heavier the object, the more the spring stretches, as described in Hooke's law. Other types of scales making use of different physical principles also exist. Some scales can be calibrated to read in units of force (weight) such as newtons instead of unit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
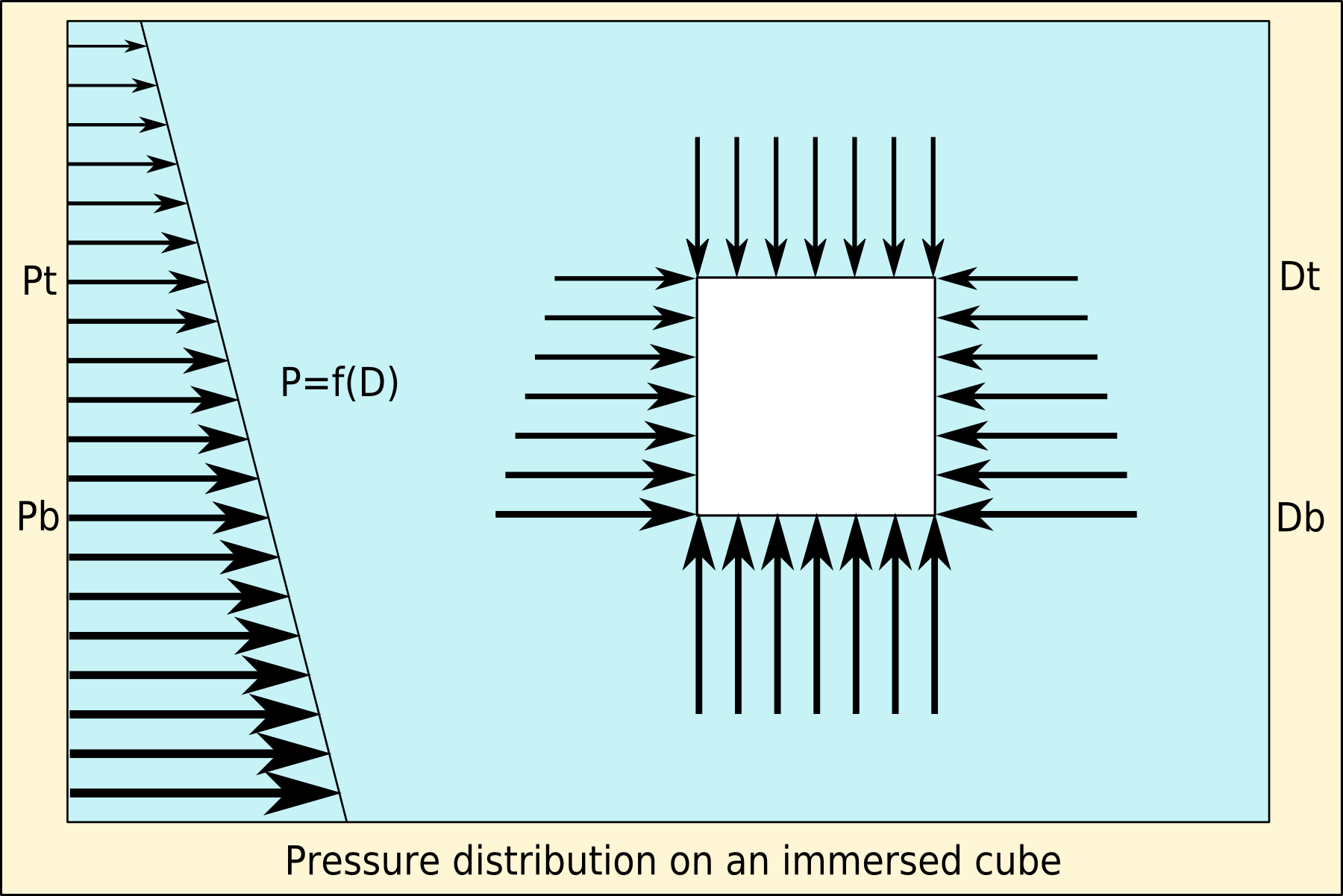
Archimedes' Principle
Archimedes' principle (also spelled Archimedes's principle) states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse. Explanation In ''On Floating Bodies'', Archimedes suggested that (c. 246 BC): Archimedes' principle allows the buoyancy of any floating object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant—that is, it remains in place without either rising ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greater Khorasan
Greater Khorāsān,Dabeersiaghi, Commentary on Safarnâma-e Nâsir Khusraw, 6th Ed. Tehran, Zavvâr: 1375 (Solar Hijri Calendar) 235–236 or Khorāsān ( pal, Xwarāsān; fa, خراسان ), is a historical eastern region in the Iranian Plateau between Western and Central Asia. The name ''Khorāsān'' is Persian and means "where the sun arrives from" or "the Eastern Province".Sykes, M. (1914). "Khorasan: The Eastern Province of Persia". ''Journal of the Royal Society of Arts'', 62(3196), 279-286.A compound of ''khwar'' (meaning "sun") and ''āsān'' (from ''āyān'', literally meaning "to come" or "coming" or "about to come"). Thus the name ''Khorasan'' (or ''Khorāyān'' ) means "sunrise", viz. " Orient, East"Humbach, Helmut, and Djelani Davari, "Nāmé Xorāsān", Johannes Gutenberg-Universität Mainz; Persian translation by Djelani Davari, published in Iranian Languages Studies Website. MacKenzie, D. (1971). ''A Concise Pahlavi Dictionary'' (p. 95). London: Oxford University ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jalali Calendar
The Jalali calendar is a solar calendar, was compiled during the reign of Jalaluddin Malik-Shah I of Seljuk by the order of Nizam al-Mulk and the place of observation were the cities of Isfahan (the capital of the Seljuks), Rey, and Nishapur. Variants of the Jalali calendar are still in use today in Iran and Afghanistan. In Iran, the Persian names of the zodiac are used while in Afghanistan the original Arabic names are used. It gains approximately 1 day on the Julian calendar every 128 years. The tropical Jalali calendar ( fa, گاهشماری جلالی or تقویم جلالی), which inherited some aspects from the Yazdgerdi calendar, was adopted on 15 March 1079 by the Seljuk Sultan Jalal al-Din Malik Shah I (for whom it was named), based on the recommendations of a committee of astronomers, including Omar Khayyam, at the imperial observatory in his capital city of Isfahan. Month computations were based on solar transits through the zodiac. It remained in use for eight ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12th-century Iranian Astronomers
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dinar
The dinar () is the principal currency unit in several countries near the Mediterranean Sea, and its historical use is even more widespread. The modern dinar's historical antecedents are the gold dinar and the silver dirham, the main coin of the medieval Islamic empires, first issued in AH 77 (696–697 CE) by Caliph Abd al-Malik ibn Marwan. The word "dinar" derives from the Latin " ''dēnārius''," a silver coin of ancient Rome, which was first minted about c.211 BCE. The English word "dinar" is the transliteration of the Arabic دينار (''dīnār''), which was borrowed via the Syriac ''dīnarā'', itself from the Latin ''dēnārius''. The Kushan Empire introduced a gold coin known as the ''dīnāra'' into India in the 1st century AD; the Gupta Empire and its successors up to the 6th century adopted the coin. The modern gold dinar is a projected bullion gold coin, not issued as official currency by any state. Legal tender Countries currently usi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
12th-century Alchemists
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. In conventions of sign where zero is considered neither positive nor negative, 1 is the first and smallest positive integer. It is also sometimes considered the first of the infinite sequence of natural numbers, followed by 2, although by other definitions 1 is the second natural number, following 0. The fundamental mathematical property of 1 is to be a multiplicative identity, meaning that any number multiplied by 1 equals the same number. Most if not all properties of 1 can be deduced from this. In advanced mathematics, a multiplicative identity is often denoted 1, even if it is not a number. 1 is by convention not considered a prime number; this was not universally accepted until the mid-20th century. Additionally, 1 is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |