|
Adaptive Mesh Refinement
In numerical analysis, adaptive mesh refinement (AMR) is a method of adapting the accuracy of a solution within certain sensitive or turbulent regions of simulation, dynamically and during the time the solution is being calculated. When solutions are calculated numerically, they are often limited to pre-determined quantified grids as in the Cartesian plane which constitute the computational grid, or 'mesh'. Many problems in numerical analysis, however, do not require a uniform precision in the numerical grids used for graph plotting or computational simulation, and would be better suited if specific areas of graphs which needed precision could be refined in quantification only in the regions requiring the added precision. Adaptive mesh refinement provides such a dynamic programming environment for adapting the precision of the numerical computation based on the requirements of a computation problem in specific areas of multi-dimensional graphs which need precision while leaving the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integrator
An integrator in measurement and control applications is an element whose output signal is the time integral of its input signal. It accumulates the input quantity over a defined time to produce a representative output. Integration is an important part of many engineering and scientific applications. Mechanical integrators are the oldest application, and are still used in such as metering of water flow or electric power. Electronic analogue integrators are the basis of analog computer An analog computer or analogue computer is a type of computer that uses the continuous variation aspect of physical phenomena such as electrical, mechanical, or hydraulic quantities (''analog signals'') to model the problem being solved. ...s and charge amplifiers. Integration is also performed by digital computing algorithms. In signal processing circuits :''See also Operational amplifier applications#Integration and differentiation, Integrator at op amp applications'' An electronics, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information". The subdivided regions may be square or rectangular, or may have arbitrary shapes. This data structure was named a quadtree by Raphael Finkel and J.L. Bentley in 1974. A similar partitioning is also known as a ''Q-tree''. All forms of quadtrees share some common features: * They decompose space into adaptable cells * Each cell (or bucket) has a maximum capacity. When maximum capacity is reached, the bucket splits * The tree directory follows the spatial decomposition of the quadtree. A tree-pyramid (T-pyramid) is a "complete" tree; every node of the T-pyramid has four child nodes exc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multigrid Method
In numerical analysis, a multigrid method (MG method) is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners. The main idea of multigrid is to accelerate the convergence of a basic iterative method (known as relaxation, which generally reduces short-wavelength error) by a ''global'' correction of the fine grid solution approximation from time to time, accomplished by solving a coarse problem. The coarse problem, while cheaper to solve, is similar to the fine grid problem in that it also has short- and long-wavelength error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cactus Framework
Cactus is an open-source, problem-solving environment designed for scientists and engineers. Its modular structure enables parallel computation across different architectures and collaborative code development between different groups. Cactus originated in the academic research community, where it was developed and used over many years by a large international collaboration of physicists and computational scientists. The name Cactus comes from the design of a central core (or "flesh") which connects to application modules (or "thorns") through an extensible interface. Thorns can implement custom developed scientific or engineering applications, such as computational fluid dynamics. Other thorns from a standard computational toolkit provide a range of computational capabilities, such as parallel I/O, data distribution, or checkpointing. Cactus runs on many architectures. Applications, developed on standard workstations or laptops, can be seamlessly run on clusters or supercom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Stepsize
In mathematics and numerical analysis, an adaptive step size is used in some methods for the numerical solution of ordinary differential equations (including the special case of numerical integration) in order to control the errors of the method and to ensure stability properties such as A-stability. Using an adaptive stepsize is of particular importance when there is a large variation in the size of the derivative. For example, when modeling the motion of a satellite about the earth as a standard Kepler orbit, a fixed time-stepping method such as the Euler method may be sufficient. However things are more difficult if one wishes to model the motion of a spacecraft taking into account both the Earth and the Moon as in the Three-body problem. There, scenarios emerge where one can take large time steps when the spacecraft is far from the Earth and Moon, but if the spacecraft gets close to colliding with one of the planetary bodies, then small time steps are needed. Romberg's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smoothed Particle Hydrodynamics
Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating the mechanics of continuum media, such as solid mechanics and fluid flows. It was developed by Gingold and Monaghan and Lucy in 1977, initially for astrophysical problems. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography. It is a meshfree Lagrangian method (where the co-ordinates move with the fluid), and the resolution of the method can easily be adjusted with respect to variables such as density. Method Advantages * By construction, SPH is a meshfree method, which makes it ideally suited to simulate problems dominated by complex boundary dynamics, like free surface flows, or large boundary displacement. * The lack of a mesh significantly simplifies the model implementation and its parallelization, even for many-core architectures. * SPH can be easily extended to a wide variety of fields, and hybridized with some other mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
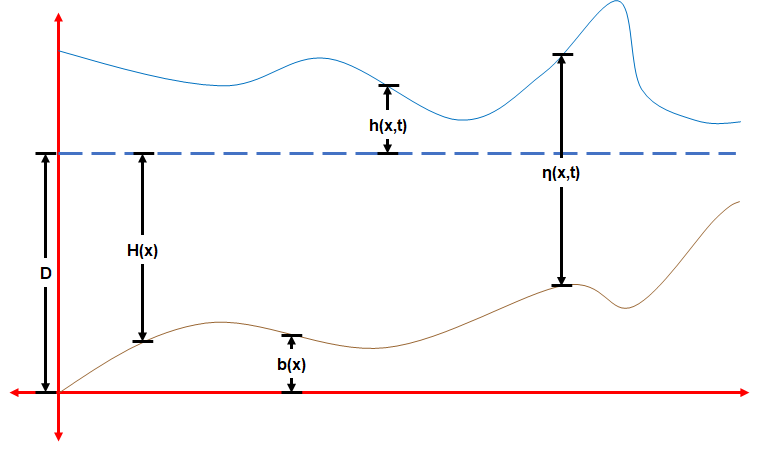
Shallow Water Equations
The shallow-water equations (SWE) are a set of hyperbolic partial differential equations (or parabolic if viscous shear is considered) that describe the flow below a pressure surface in a fluid (sometimes, but not necessarily, a free surface). The shallow-water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant (see the related section below). The equations are derived from depth-integrating the Navier–Stokes equations, in the case where the horizontal length scale is much greater than the vertical length scale. Under this condition, conservation of mass implies that the vertical velocity scale of the fluid is small compared to the horizontal velocity scale. It can be shown from the momentum equation that vertical pressure gradients are nearly hydrostatic, and that horizontal pressure gradients are due to the displacement of the pressure surface, implying that the horizontal velocity field is const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the spoke of a chariot wheel. as a function of axial position ../nowiki>" Spherical coordinates In a spherical coordinate system, the radius describes the distance of a point from a fixed origin. Its position if further defined by the polar angle measured between the radial direction and a fixed zenith direction, and the azimuth angle, the angle between the orthogonal projection of the radial direction on a reference plane that passes through the origin and is orthogonal to the zenith, and a fixed reference direction in that plane. See also *Bend radius *Filling radius in Riemannian geometry *Radius of convergence * Radius of convexity *Radius of curvature *Radius of gyration ''Radius of gyration'' or gyradius of a body about the axis of r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Giant Molecular Cloud
A molecular cloud, sometimes called a stellar nursery (if star formation is occurring within), is a type of interstellar cloud, the density and size of which permit absorption nebulae, the formation of molecules (most commonly molecular hydrogen, H2), and the formation of H II regions. This is in contrast to other areas of the interstellar medium that contain predominantly ionized gas. Molecular hydrogen is difficult to detect by infrared and radio observations, so the molecule most often used to determine the presence of H2 is carbon monoxide (CO). The ratio between CO luminosity and H2 mass is thought to be constant, although there are reasons to doubt this assumption in observations of some other galaxy, galaxies. Within molecular clouds are regions with higher density, where much dust and many gas cores reside, called clumps. These clumps are the beginning of star formation if gravitational forces are sufficient to cause the dust and gas to collapse. History The form of mole ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astrophysics
Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline said, Astrophysics "seeks to ascertain the nature of the heavenly bodies, rather than their positions or motions in space–''what'' they are, rather than ''where'' they are." Among the subjects studied are the Sun, other stars, galaxies, extrasolar planets, the interstellar medium and the cosmic microwave background. Emissions from these objects are examined across all parts of the electromagnetic spectrum, and the properties examined include luminosity, density, temperature, and chemical composition. Because astrophysics is a very broad subject, ''astrophysicists'' apply concepts and methods from many disciplines of physics, including classical mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum mechanics, relativity, nuclear and particle physics, and atomic a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Grid
A regular grid is a tessellation of ''n''-dimensional Euclidean space by congruent parallelotopes (e.g. bricks). Its opposite is irregular grid. Grids of this type appear on graph paper and may be used in finite element analysis, finite volume methods, finite difference methods, and in general for discretization of parameter spaces. Since the derivatives of field variables can be conveniently expressed as finite differences, structured grids mainly appear in finite difference methods. Unstructured grids offer more flexibility than structured grids and hence are very useful in finite element and finite volume methods. Each cell in the grid can be addressed by index (i, j) in two dimensions or (i, j, k) in three dimensions, and each vertex has coordinates (i\cdot dx, j\cdot dy) in 2D or (i\cdot dx, j\cdot dy, k\cdot dz) in 3D for some real numbers ''dx'', ''dy'', and ''dz'' representing the grid spacing. Related grids A Cartesian grid is a special case where the elements are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |