|
Z Scores
In statistics, the standard score is the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured. Raw scores above the mean have positive standard scores, while those below the mean have negative standard scores. It is calculated by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation. This process of converting a raw score into a standard score is called standardizing or normalizing (however, "normalizing" can refer to many types of ratios; see normalization for more). Standard scores are most commonly called ''z''-scores; the two terms may be used interchangeably, as they are in this article. Other equivalent terms in use include z-values, normal scores, standardized variables and pull in high energy physics. Computing a z-score requires knowledge of the mean and standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Normal Distribution
''The'' () is a grammatical article in English, denoting persons or things already mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with pronouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of pronoun ''thee'') when followed by a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prediction Interval
In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which a future observation will fall, with a certain probability, given what has already been observed. Prediction intervals are often used in regression analysis. Prediction intervals are used in both frequentist statistics and Bayesian statistics: a prediction interval bears the same relationship to a future observation that a frequentist confidence interval or Bayesian credible interval bears to an unobservable population parameter: prediction intervals predict the distribution of individual future points, whereas confidence intervals and credible intervals of parameters predict the distribution of estimates of the true population mean or other quantity of interest that cannot be observed. Introduction For example, if one makes the parametric assumption that the underlying distribution is a normal distribution, and has a sample set , then confidence intervals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Omega Ratio
The Omega ratio is a risk-return performance measure of an investment asset, portfolio, or strategy. It was devised by Con Keating and William F. Shadwick in 2002 and is defined as the probability weighted ratio of gains versus losses for some threshold return target. The ratio is an alternative for the widely used Sharpe ratio and is based on information the Sharpe ratio discards. Omega is calculated by creating a partition in the cumulative return distribution in order to create an area of losses and an area for gains relative to this threshold. The ratio is calculated as: : \Omega(\theta) = \frac, where F is the cumulative probability distribution function of the returns and \theta is the target return threshold defining what is considered a gain versus a loss. A larger ratio indicates that the asset provides more gains relative to losses for some threshold \theta and so would be preferred by an investor. When \theta is set to zero the gain-loss-ratio by Bernardo and Ledoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample Mean
The sample mean (or "empirical mean") and the sample covariance are statistics computed from a Sample (statistics), sample of data on one or more random variables. The sample mean is the average value (or mean, mean value) of a sample (statistics), sample of numbers taken from a larger Statistical population, population of numbers, where "population" indicates not number of people but the entirety of relevant data, whether collected or not. A sample of 40 companies' sales from the Fortune 500 might be used for convenience instead of looking at the population, all 500 companies' sales. The sample mean is used as an estimator for the population mean, the average value in the entire population, where the estimate is more likely to be close to the population mean if the sample is large and representative. The reliability of the sample mean is estimated using the standard error, which in turn is calculated using the variance of the sample. If the sample is random, the standard error fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to end th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a random var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Statistics
Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory. Introduction Statistical data collection is concerned with the planning of studies, especially with the design of randomized experiments and with the planning of surveys using random sampling. The initial analysis of the data often follows the study protocol specified prior to the study being conducted. The data from a study can also be analyzed to consider secondary hypotheses inspired by the initial results, or to suggest new studies. A secondary analysis of the data from a planned study uses tools from data analysis, and the process of doing this is mathematical statistics. Data analysis is divided into: * descriptive statistics - the part of st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
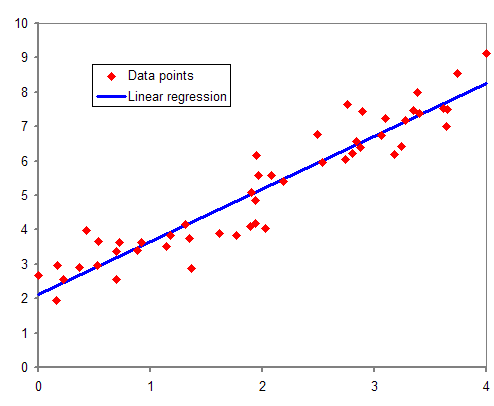
Multiple Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given set o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Z Score For Student B
Z (or z) is the 26th and last letter of the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its usual names in English are ''zed'' () and ''zee'' (), with an occasional archaic variant ''izzard'' ()."Z", ''Oxford English Dictionary,'' 2nd edition (1989); ''Merriam-Webster's Third New International Dictionary of the English Language, Unabridged'' (1993); "zee", ''op. cit''. Name and pronunciation In most English-speaking countries, including Australia, Canada, India, Ireland, New Zealand and the United Kingdom, the letter's name is ''zed'' , reflecting its derivation from the Greek ''zeta'' (this dates to Latin, which borrowed Y and Z from Greek), but in American English its name is ''zee'' , analogous to the names for B, C, D, etc., and deriving from a late 17th-century English dialectal form. Another English dialectal form is ''izzard'' . This dates from the mid-18th century and probably derives fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ACT (test)
The ACT (; originally an abbreviation of American College Testing) Name changed in 1996. is a standardized test used for University and college admissions, college admissions in the Education in the United States, United States. It is currently administered by ACT (nonprofit organization), ACT, a nonprofit organization of the same name. The ACT test covers four academic skill areas: English studies, English, mathematics, Reading (process), reading, and reasoning, scientific reasoning. It also offers an optional direct writing test. It is accepted by all four-year colleges and universities in the United States as well as more than 225 universities outside of the U.S. The main four ACT test sections are individually Test score, scored on a scale of 1–36, and a composite score (the rounded whole number average of the four sections) is provided. The ACT was first introduced in November of 1959 by University of Iowa professor Everett Franklin Lindquist as a competitor to the SA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Z Score For Students A
Z (or z) is the 26th and last letter of the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its usual names in English are ''zed'' () and ''zee'' (), with an occasional archaic variant ''izzard'' ()."Z", ''Oxford English Dictionary,'' 2nd edition (1989); ''Merriam-Webster's Third New International Dictionary of the English Language, Unabridged'' (1993); "zee", ''op. cit''. Name and pronunciation In most English-speaking countries, including Australia, Canada, India, Ireland, New Zealand and the United Kingdom, the letter's name is ''zed'' , reflecting its derivation from the Greek ''zeta'' (this dates to Latin, which borrowed Y and Z from Greek), but in American English its name is ''zee'' , analogous to the names for B, C, D, etc., and deriving from a late 17th-century English dialectal form. Another English dialectal form is ''izzard'' . This dates from the mid-18th century and probably derives fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)