|
Young–Fibonacci Lattice
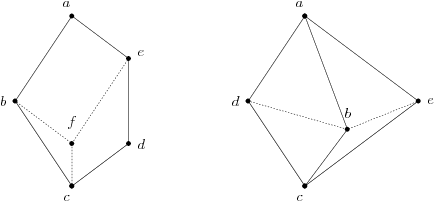
In mathematics, the Young–Fibonacci graph and Young–Fibonacci lattice, named after Alfred Young and Leonardo Fibonacci, are two closely related structures involving sequences of the digits 1 and 2. Any digit sequence of this type can be assigned a ''rank'', the sum of its digits: for instance, the rank of 11212 is 1 + 1 + 2 + 1 + 2 = 7. As was already known in ancient India, the number of sequences with a given rank is a Fibonacci number. The Young–Fibonacci lattice is an infinite modular lattice having these digit sequences as its elements, compatible with this rank structure. The Young–Fibonacci graph is the graph of this lattice, and has a vertex for each digit sequence. As the graph of a modular lattice, it is a modular graph. The Young–Fibonacci graph and the Young–Fibonacci lattice were both initially studied in two papers by and . They are named after the closely related Young's lattice and after the Fibonacci n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undirected Graph
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called '' vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then this graph is directed, because owing money is not necessarily reciprocated. Gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorics On Words
Combinatorics on words is a fairly new field of mathematics, branching from combinatorics, which focuses on the study of words and formal languages. The subject looks at letters or symbols, and the sequences they form. Combinatorics on words affects various areas of mathematical study, including algebra and computer science. There have been a wide range of contributions to the field. Some of the first work was on square-free words by Axel Thue in the early 1900s. He and colleagues observed patterns within words and tried to explain them. As time went on, combinatorics on words became useful in the study of algorithms and coding. It led to developments in abstract algebra and answering open questions. Definition Combinatorics is an area of discrete mathematics. Discrete mathematics is the study of countable structures. These objects have a definite beginning and end. The study of enumerable objects is the opposite of disciplines such as analysis, where calculus and i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Numbers
In mathematics, the Fibonacci sequence is a sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 and some (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the sequence begins : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... The Fibonacci numbers were first described in Indian mathematics as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book . Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the '' Fibonacci Quarterly''. Applications of Fibon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Theory
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bound or join) and a unique infimum (also called a greatest lower bound or meet). An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor. Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilattices include lattices, which in turn include Heyting and Boolean algebras. These ''lattice-like'' structur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributive Lattice
In mathematics, a distributive lattice is a lattice (order), lattice in which the operations of join and meet distributivity, distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union (set theory), union and intersection (set theory), intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to order isomorphism, isomorphism—given as such a lattice of sets. Definition As in the case of arbitrary lattices, one can choose to consider a distributive lattice ''L'' either as a structure of order theory or of universal algebra. Both views and their mutual correspondence are discussed in the article on lattice (order), lattices. In the present situation, the algebraic description appears to be more convenient. A lattice (''L'',∨,∧) is distributive if the following additional identity holds for all ''x'', ''y'', and ''z'' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (order)
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bound or join (mathematics), join) and a unique infimum (also called a greatest lower bound or meet (mathematics), meet). An example is given by the power set of a set, partially ordered by Subset, inclusion, for which the supremum is the Union (set theory), union and the infimum is the Intersection (set theory), intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor. Lattices can also be characterized as algebraic structures satisfying certain axiomatic Identity (mathematics), identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilatti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Order
In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word ''partial'' is used to indicate that not every pair of elements needs to be comparable; that is, there may be pairs for which neither element precedes the other. Partial orders thus generalize total orders, in which every pair is comparable. Formally, a partial order is a homogeneous binary relation that is reflexive, antisymmetric, and transitive. A partially ordered set (poset for short) is an ordered pair P=(X,\leq) consisting of a set X (called the ''ground set'' of P) and a partial order \leq on X. When the meaning is clear from context and there is no ambiguity about the partial order, the set X itself is sometimes called a poset. Partial order relations The term ''partial order'' usually refers to the reflexive partial order relations, referred to in this article as ''non-strict'' partial orders. However som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transitive Closure
In mathematics, the transitive closure of a homogeneous binary relation on a set (mathematics), set is the smallest Relation (mathematics), relation on that contains and is Transitive relation, transitive. For finite sets, "smallest" can be taken in its usual sense, of having the fewest related pairs; for infinite sets is the unique minimal element, minimal transitive superset of . For example, if is a set of airports and means "there is a direct flight from airport to airport " (for and in ), then the transitive closure of on is the relation such that means "it is possible to fly from to in one or more flights". More formally, the transitive closure of a binary relation on a set is the smallest (w.r.t. ⊆) transitive relation on such that ⊆ ; see . We have = if, and only if, itself is transitive. Conversely, transitive reduction adduces a minimal relation from a given relation such that they have the same closure, that is, ; however, many differen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Poset
In mathematics, a differential poset is a partially ordered set (or ''poset'' for short) satisfying certain local properties. (The formal definition is given below.) This family of posets was introduced by as a generalization of Young's lattice (the poset of integer partitions ordered by inclusion), many of whose combinatorial properties are shared by all differential posets. In addition to Young's lattice, the other most significant example of a differential poset is the Young–Fibonacci lattice. Definitions A poset ''P'' is said to be a ''differential poset'', and in particular to be ''r''-''differential'' (where ''r'' is a positive integer), if it satisfies the following conditions: * ''P'' is graded and locally finite with a unique minimal element; * for every two distinct elements ''x'', ''y'' of ''P'', the number of elements covering both ''x'' and ''y'' is the same as the number of elements covered by both ''x'' and ''y''; and * for every element ''x'' of ''P'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connectivity (graph Theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more Connected component (graph theory), isolated subgraphs. It is closely related to the theory of flow network, network flow problems. The connectivity of a graph is an important measure of its resilience as a network. Connected vertices and graphs In an undirected graph , two vertex (graph theory), vertices and are called connected if contains a Path (graph theory), path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length (that is, they are the endpoints of a single edge), the vertices are called adjacent. A Graph (discrete mathematics), graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a Path (graph theory), path between every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |