|
Wrapped Normal Distribution
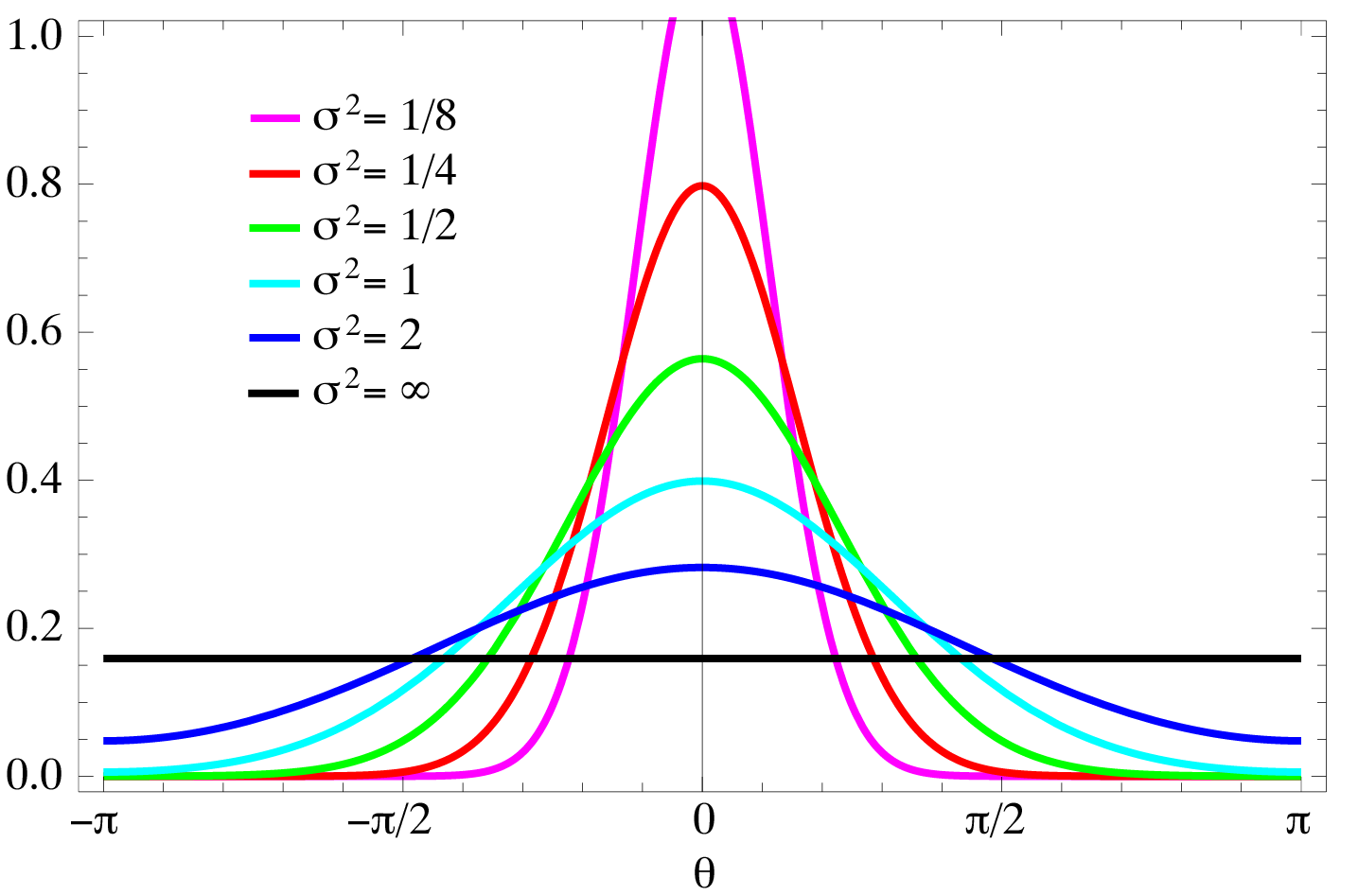
In probability theory and directional statistics, a wrapped normal distribution is a wrapped probability distribution that results from the "wrapping" of the normal distribution around the unit circle. It finds application in the theory of Brownian motion and is a solution to the heat equation for periodic boundary conditions. It is closely approximated by the von Mises distribution, which, due to its mathematical simplicity and tractability, is the most commonly used distribution in directional statistics. Definition The probability density function of the wrapped normal distribution is : f_(\theta;\mu,\sigma)=\frac \sum^_ \exp \left frac \right where ''μ'' and ''σ'' are the mean and standard deviation of the unwrapped distribution, respectively. Expressing the above density function in terms of the characteristic function of the normal distribution yields: : f_(\theta;\mu,\sigma)=\frac\sum_^\infty e^ =\frac\vartheta\left(\frac,\frac\right) , where \vartheta(\theta,\tau) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Function (probability Theory)
In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform (with sign reversal) of the probability density function. Thus it provides an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables. In addition to univariate distributions, characteristic functions can be defined for vector- or matrix-valued random variables, and can also be extended to more generic cases. The characteristic function always exists when treated as a function of a real-valued argument, unlike the moment-generating function. There are relations between the behavior of the charact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Distributions
Continuity or continuous may refer to: Mathematics * Continuity (mathematics), the opposing concept to discreteness; common examples include ** Continuous probability distribution or random variable in probability and statistics ** Continuous game, a generalization of games used in game theory ** Law of continuity, a heuristic principle of Gottfried Leibniz * Continuous function, in particular: ** Continuity (topology), a generalization to functions between topological spaces ** Scott continuity, for functions between posets ** Continuity (set theory), for functions between ordinals ** Continuity (category theory), for functors ** Graph continuity, for payoff functions in game theory * Continuity theorem may refer to one of two results: ** Lévy's continuity theorem, on random variables ** Kolmogorov continuity theorem, on stochastic processes * In geometry: ** Parametric continuity, for parametrised curves ** Geometric continuity, a concept primarily applied to the conic section ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Mises Distribution
In probability theory and directional statistics, the Richard von Mises, von Mises distribution (also known as the circular normal distribution or the Andrey Nikolayevich Tikhonov, Tikhonov distribution) is a continuous probability distribution on the circle. It is a close approximation to the wrapped normal distribution, which is the circular analogue of the normal distribution. A freely diffusing angle \theta on a circle is a wrapped normally distributed random variable with an Phase unwrapping, unwrapped variance that grows linearly in time. On the other hand, the von Mises distribution is the stationary distribution of a drift and diffusion process on the circle in a harmonic potential, i.e. with a preferred orientation. The von Mises distribution is the Maximum entropy probability distribution, maximum entropy distribution for circular data when the real and imaginary parts of the first Directional statistics, circular moment are specified. The von Mises distribution is a spe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wrapped Cauchy Distribution
In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution. The wrapped Cauchy distribution is often found in the field of spectroscopy where it is used to analyze diffraction patterns (e.g. see Fabry–Pérot interferometer). Description The probability density function of the wrapped Cauchy distribution is: : f_(\theta;\mu,\gamma)=\sum_^\infty \frac\qquad -\pi<\theta<\pi where is the scale factor and is the peak position of the "unwrapped" distribution. Expressing the above pdf in terms of the |
Dirac Comb
In mathematics, a Dirac comb (also known as sha function, impulse train or sampling function) is a periodic function, periodic Function (mathematics), function with the formula \operatorname_(t) \ := \sum_^ \delta(t - k T) for some given period T. Here ''t'' is a real variable and the sum extends over all integers ''k.'' The Dirac delta function \delta and the Dirac comb are Distribution_(mathematics)#Tempered_distributions_and_Fourier_transform, tempered distributions. The graph of the function resembles a comb (with the \deltas as the comb's ''teeth''), hence its name and the use of the comb-like Cyrillic script, Cyrillic letter Sha (Cyrillic), sha (Ш) to denote the function. The symbol \operatorname\,\,(t), where the period is omitted, represents a Dirac comb of unit period. This implies \operatorname_(t) \ = \frac\operatorname\ \!\!\!\left(\frac\right). Because the Dirac comb function is periodic, it can be represented as a Fourier series based on the Dirichlet kernel: \o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Series
A Fourier series () is an Series expansion, expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always Convergent series, converge. Well-behaved functions, for example Smoothness, smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Function
In mathematics, the Euler function is given by :\phi(q)=\prod_^\infty (1-q^k),\quad , q, <1. Named after Leonhard Euler, it is a model example of a q-series, ''q''-series and provides the prototypical example of a relation between combinatorics and complex analysis. Properties The coefficient in the formal power series expansion for gives the number of Partition of an integer, partitions of ''k''. That is, : where is the Partition function (number theory), partition function. The Euler identity, also known as the Pentagonal number theorem, is : is a pentagonal number. The Euler function is related to the Dedekind eta function as : The Euler function may be expressed as a q-Pochhammer symbol, ''q''-Pochhammer symbol: : ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to[0, 1], the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or "shannon (unit), shannons"), while base Euler's number, ''e'' gives "natural units" nat (unit), nat, and base 10 gives units of "dits", "bans", or "Hartley (unit), hartleys". An equivalent definition of entropy is the expected value of the self-information of a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A Course Of Modern Analysis
''A Course of Modern Analysis: an introduction to the general theory of infinite processes and of analytic functions; with an account of the principal transcendental functions'' (colloquially known as Whittaker and Watson) is a landmark textbook on mathematical analysis written by Edmund T. Whittaker and George N. Watson, first published by Cambridge University Press in 1915. The first edition was Whittaker's alone, but later editions were co-authored with Watson. History Its first, second, third, and the fourth edition were published in 1902, 1915, 1920, and 1927, respectively. Since then, it has continuously been reprinted and is still in print today. A revised, expanded and digitally reset fifth edition, edited by Victor H. Moll, was published in 2021. The book is notable for being the standard reference and textbook for a generation of Cambridge mathematicians including Littlewood and Godfrey H. Hardy. Mary L. Cartwright studied it as preparation for her final hono ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobi Triple Product
In mathematics, the Jacobi triple product is the identity: :\prod_^\infty \left( 1 - x^\right) \left( 1 + x^ y^2\right) \left( 1 +\frac\right) = \sum_^\infty x^ y^, for complex numbers ''x'' and ''y'', with , ''x'', < 1 and ''y'' ≠ 0. It was introduced by in his work '' Fundamenta Nova Theoriae Functionum Ellipticarum''. The Jacobi triple product identity is the Macdonald identity for the affine root system of type ''A''1, and is the Weyl denominator formula for the corresponding affine Kac–Moody algebra. Properties Jacobi's proof relies on Euler's pentagonal number theorem, which is itself a specific case of the Jacobi triple product identity. Let x=q\sqrt q and y^2=-\sqrt. Then we have :\phi(q) = \prod_^\infty \left(1-q^m \right) = \sum_^\infty (-1)^n q^. The Rogers–Ramanujan identities follow with x=q^2\sqrt q, y^2=-\sqrt and x=q^2\sqrt q, y^2=-q\sqrt. The Jacobi Triple Product also allows the Jacobi theta function to be written as an infinite product a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wrapped Distribution
In probability theory and directional statistics, a wrapped probability distribution is a continuous probability distribution that describes data points that lie on a unit n-sphere, ''n''-sphere. In one dimension, a wrapped distribution consists of points on the unit circle. If \phi is a random variate in the interval (-\infty,\infty) with probability density function (PDF) p(\phi), then z = e^ is a circular variable distributed according to the wrapped distribution p_(\theta) and \theta = \arg(z) is an angular variable in the interval (-\pi,\pi] distributed according to the wrapped distribution p_w(\theta). Any probability density function p(\phi) on the line can be "wrapped" around the circumference of a circle of unit radius. That is, the PDF of the wrapped variable :\theta=\phi \mod 2\pi in some interval of length 2\pi is : p_w(\theta)=\sum_^\infty which is a periodic summation, periodic sum of period 2\pi. The preferred interval is generally (-\pi<\theta\le\pi) for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |