|
Wilks' Theorem
In statistics Wilks' theorem offers an asymptotic distribution of the log-likelihood ratio statistic, which can be used to produce confidence intervals for maximum-likelihood estimates or as a test statistic for performing the likelihood-ratio test. Statistical tests (such as hypothesis testing) generally require knowledge of the probability distribution of the test statistic. This is often a problem for likelihood ratios, where the probability distribution can be very difficult to determine. A convenient result by Samuel S. Wilks says that as the sample size approaches \infty, the distribution of the test statistic -2 \log(\Lambda) asymptotically approaches the chi-squared (\chi^2) distribution under the null hypothesis H_0. Here, \Lambda denotes the likelihood ratio, and the \chi^2 distribution has degrees of freedom equal to the difference in dimensionality of \Theta and \Theta_0, where \Theta is the full parameter space and \Theta_0 is the subset of the parameter space asso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter Space
The parameter space is the space of possible parameter values that define a particular mathematical model, often a subset of finite-dimensional Euclidean space. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function. The ranges of values of the parameters may form the axes of a plot, and particular outcomes of the model may be plotted against these axes to illustrate how different regions of the parameter space produce different types of behavior in the model. In statistics, parameter spaces are particularly useful for describing parametric families of probability distributions. They also form the background for parameter estimation. In the case of extremum estimators for parametric models, a certain objective function is maximized or minimized over the parameter space. Theorems of existence and consistency of such estimators require some assumptions about the topology of the parameter space. For instance, com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayes Factor
The Bayes factor is a ratio of two competing statistical models represented by their marginal likelihood, and is used to quantify the support for one model over the other. The models in questions can have a common set of parameters, such as a null hypothesis and an alternative, but this is not necessary; for instance, it could also be a non-linear model compared to its linear approximation. The Bayes factor can be thought of as a Bayesian analog to the likelihood-ratio test, but since it uses the (integrated) marginal likelihood instead of the maximized likelihood, both tests only coincide under simple hypotheses (e.g., two specific parameter values). Also, in contrast with null hypothesis significance testing, Bayes factors support evaluation of evidence ''in favor'' of a null hypothesis, rather than only allowing the null to be rejected or not rejected. Although conceptually simple, the computation of the Bayes factor can be challenging depending on the complexity of the model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and graphics supported by the R Core Team and the R Foundation for Statistical Computing. Created by statisticians Ross Ihaka and Robert Gentleman, R is used among data miners, bioinformaticians and statisticians for data analysis and developing statistical software. Users have created packages to augment the functions of the R language. According to user surveys and studies of scholarly literature databases, R is one of the most commonly used programming languages used in data mining. R ranks 12th in the TIOBE index, a measure of programming language popularity, in which the language peaked in 8th place in August 2020. The official R software environment is an open-source free software environment within the GNU package, available under the GNU General Public License. It is written primarily in C, Fortran, and R itself (partially self-hosting). Precompiled executables are provided for various operating systems. R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom
Degrees of freedom (often abbreviated df or DOF) refers to the number of independent variables or parameters of a thermodynamic system. In various scientific fields, the word "freedom" is used to describe the limits to which physical movement or other physical processes are possible. This relates to the philosophical concept to the extent that people may be considered to have as much freedom as they are physically able to exercise. Applications Statistics In statistics, degrees of freedom refers to the number of variables in a statistic calculation that can vary. It can be calculated by subtracting the number of estimated parameters from the total number of values in the sample. For example, a sample variance calculation based on n samples will have n-1 degrees of freedom, because sample variance is calculated using the sample mean as an estimate of the actual mean. Mathematics In mathematics, this notion is formalized as the dimension of a manifold or an algebraic variety. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Restricted Maximum Likelihood
In statistics, the restricted (or residual, or reduced) maximum likelihood (REML) approach is a particular form of maximum likelihood estimation that does not base estimates on a maximum likelihood fit of all the information, but instead uses a likelihood function calculated from a transformed set of data, so that nuisance parameters have no effect. (see REML) In the case of variance component estimation, the original data set is replaced by a set of contrasts calculated from the data, and the likelihood function is calculated from the probability distribution of these contrasts, according to the model for the complete data set. In particular, REML is used as a method for fitting linear mixed models. In contrast to the earlier maximum likelihood estimation, REML can produce unbiased estimates of variance and covariance parameters. The idea underlying REML estimation was put forward by M. S. Bartlett in 1937. The first description of the approach applied to estimating components of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
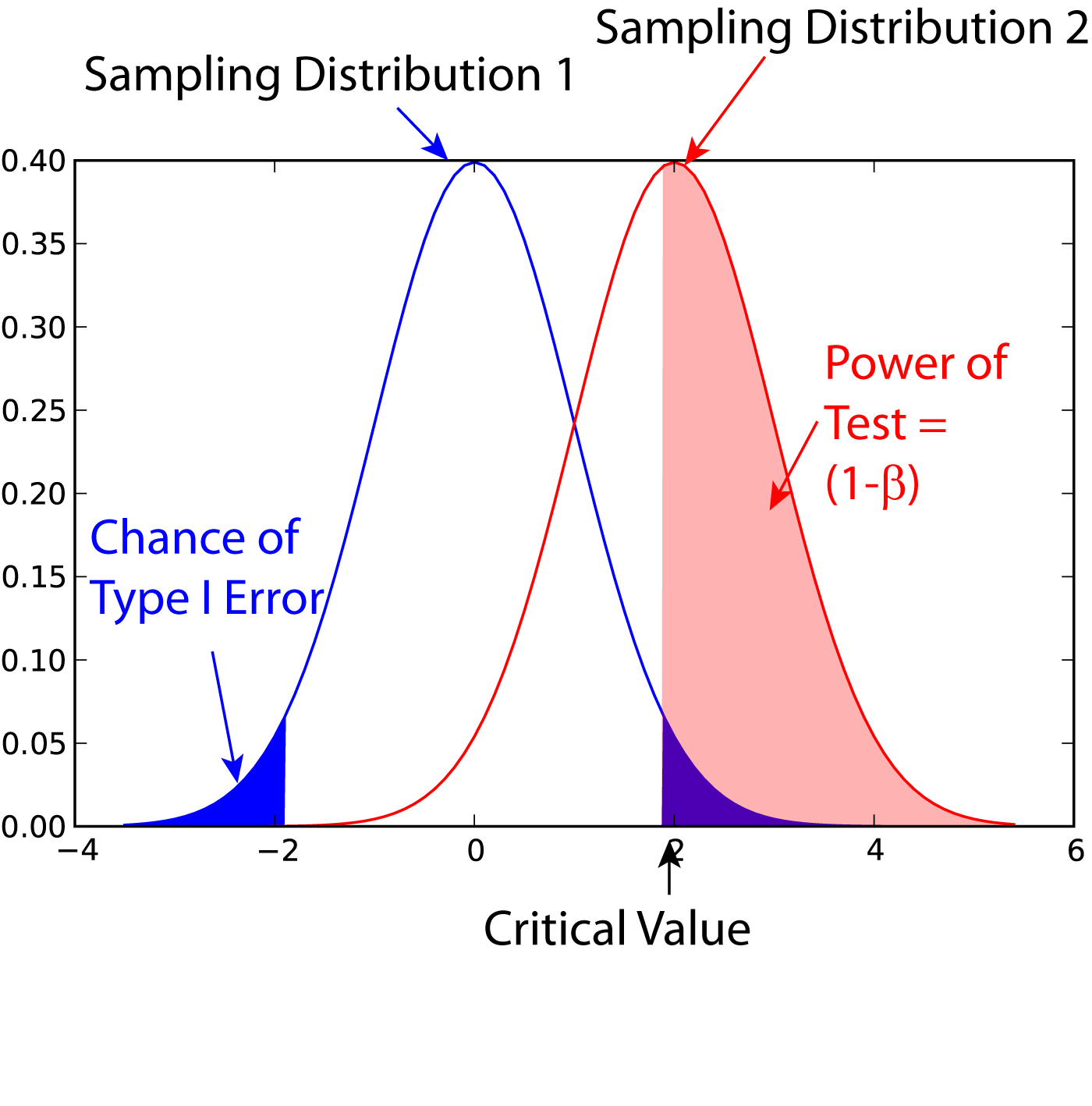
Statistical Power
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixed Model
A mixed model, mixed-effects model or mixed error-component model is a statistical model containing both fixed effects and random effects. These models are useful in a wide variety of disciplines in the physical, biological and social sciences. They are particularly useful in settings where repeated measurements are made on the same statistical units (longitudinal study), or where measurements are made on clusters of related statistical units. Because of their advantage in dealing with missing values, mixed effects models are often preferred over more traditional approaches such as repeated measures analysis of variance. This page will discuss mainly linear mixed-effects models (LMEM) rather than generalized linear mixed models or nonlinear mixed-effects models. History and current status Ronald Fisher introduced random effects models to study the correlations of trait values between relatives. In the 1950s, Charles Roy Henderson provided best linear unbiased estimates of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Effects Model
In statistics, a random effects model, also called a variance components model, is a statistical model where the model parameters are random variables. It is a kind of hierarchical linear model, which assumes that the data being analysed are drawn from a hierarchy of different populations whose differences relate to that hierarchy. A random effects model is a special case of a mixed model. Contrast this to the biostatistics definitions, as biostatisticians use "fixed" and "random" effects to respectively refer to the population-average and subject-specific effects (and where the latter are generally assumed to be unknown, latent variables). Qualitative description Random effect models assist in controlling for unobserved heterogeneity when the heterogeneity is constant over time and not correlated with independent variables. This constant can be removed from longitudinal data through differencing, since taking a first difference will remove any time invariant components of the m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contingency Table
In statistics, a contingency table (also known as a cross tabulation or crosstab) is a type of table in a matrix format that displays the (multivariate) frequency distribution of the variables. They are heavily used in survey research, business intelligence, engineering, and scientific research. They provide a basic picture of the interrelation between two variables and can help find interactions between them. The term ''contingency table'' was first used by Karl Pearson in "On the Theory of Contingency and Its Relation to Association and Normal Correlation", part of the ''Drapers' Company Research Memoirs Biometric Series I'' published in 1904. A crucial problem of multivariate statistics is finding the (direct-)dependence structure underlying the variables contained in high-dimensional contingency tables. If some of the conditional independences are revealed, then even the storage of the data can be done in a smarter way (see Lauritzen (2002)). In order to do this one can use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary. Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the estimate of a parameter is called the degrees of freedom. In general, the degrees of freedom of an estimate of a parameter are equal to the number of independent scores that go into the estimate minus the number of parameters used as intermediate steps in the estimation of the parameter itself. For example, if the variance is to be estimated from a random sample of ''N'' independent scores, then the degrees of freedom is equal to the number of independent scores (''N'') minus the number of parameters estimated as intermediate steps (one, namely, the sample mean) and is therefore equal to ''N'' − 1. Mathematically, degrees of freedom is the number of dimensions of the domain o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |