|
Wess–Zumino–Witten Model
In theoretical physics and mathematics, a Wess–Zumino–Witten (WZW) model, also called a Wess–Zumino–Novikov–Witten model, is a type of two-dimensional conformal field theory named after Julius Wess, Bruno Zumino, Sergei Novikov and Edward Witten. A WZW model is associated to a Lie group (or supergroup), and its symmetry algebra is the affine Lie algebra built from the corresponding Lie algebra (or Lie superalgebra). By extension, the name WZW model is sometimes used for any conformal field theory whose symmetry algebra is an affine Lie algebra. Action Definition For \Sigma a Riemann surface, G a Lie group, and k a (generally complex) number, let us define the G-WZW model on \Sigma at the level k. The model is a nonlinear sigma model whose action is a functional of a field \gamma:\Sigma \to G: :S_k(\gamma)= -\frac \int_ d^2x\, \mathcal \left (\gamma^ \partial^\mu \gamma, \gamma^ \partial_\mu \gamma \right ) + 2\pi k S^(\gamma). Here, \Sigma is equipped with a flat Eu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena. The advancement of science generally depends on the interplay between experimental studies and theory. In some cases, theoretical physics adheres to standards of mathematical rigour while giving little weight to experiments and observations.There is some debate as to whether or not theoretical physics uses mathematics to build intuition and illustrativeness to extract physical insight (especially when normal experience fails), rather than as a tool in formalizing theories. This links to the question of it using mathematics in a less formally rigorous, and more intuitive or heuristic way than, say, mathematical physics. For example, while developing special relativity, Albert Einstein was concerned wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Killing Form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras. Cartan's criteria (criterion of solvability and criterion of semisimplicity) show that Killing form has a close relationship to the semisimplicity of the Lie algebras. History and name The Killing form was essentially introduced into Lie algebra theory by in his thesis. In a historical survey of Lie theory, has described how the term ''"Killing form"'' first occurred in 1951 during one of his own reports for the Séminaire Bourbaki; it arose as a misnomer, since the form had previously been used by Lie theorists, without a name attached. Some other authors now employ the term ''" Cartan-Killing form"''. At the end of the 19th century, Killing had noted that the coefficients of the characteristic equation of a regular semisimple element of a Lie algebra are invariant under the adjoint group, from which it follows tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pullback (differential Geometry)
Suppose that is a smooth map between smooth manifolds ''M'' and ''N''. Then there is an associated linear map from the space of 1-forms on ''N'' (the linear space of sections of the cotangent bundle) to the space of 1-forms on ''M''. This linear map is known as the pullback (by ''φ''), and is frequently denoted by ''φ''∗. More generally, any covariant tensor field – in particular any differential form – on ''N'' may be pulled back to ''M'' using ''φ''. When the map ''φ'' is a diffeomorphism, then the pullback, together with the pushforward, can be used to transform any tensor field from ''N'' to ''M'' or vice versa. In particular, if ''φ'' is a diffeomorphism between open subsets of R''n'' and R''n'', viewed as a change of coordinates (perhaps between different charts on a manifold ''M''), then the pullback and pushforward describe the transformation properties of covariant and contravariant tensors used in more traditional (coordinate dependent) approaches ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Manifold
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (division), or equivalently, the concept of addition and the taking of inverses (subtraction). Combining these two ideas, one obtains a continuous group where multiplying points and their inverses are continuous. If the multiplication and taking of inverses are smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the rotational symmetry in three dimensions (given by the special orthogonal group \text(3)). Lie groups are widely used in many parts of modern mathematics and physics. Lie g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Form
In mathematics, the exterior algebra, or Grassmann algebra, named after Hermann Grassmann, is an algebra that uses the exterior product or wedge product as its multiplication. In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors u and v, denoted by u \wedge v, is called a bivector and lives in a space called the ''exterior square'', a vector space that is distinct from the original space of vectors. The magnitude of u \wedge v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. More generally, all parallel plane surfaces with the same orientation and area have the same bivector as a measure of their oriented area. Like the cross product, the exterior product is anticommutative, meaning tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structure Constants
In mathematics, the structure constants or structure coefficients of an algebra over a field are used to explicitly specify the product of two basis vectors in the algebra as a linear combination. Given the structure constants, the resulting product is bilinear and can be uniquely extended to all vectors in the vector space, thus uniquely determining the product for the algebra. Structure constants are used whenever an explicit form for the algebra must be given. Thus, they are frequently used when discussing Lie algebras in physics, as the basis vectors indicate specific directions in physical space, or correspond to specific particles. Recall that Lie algebras are algebras over a field, with the bilinear product being given by the Lie bracket or commutator. Definition Given a set of basis vectors \ for the underlying vector space of the algebra, the structure constants or structure coefficients c_^ express the multiplication \cdot of pairs of vectors as a linear combination: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SL2(R)
In mathematics, the special linear group SL(2, R) or SL2(R) is the group of 2 × 2 real matrices with determinant one: : \mbox(2,\mathbf) = \left\. It is a connected non-compact simple real Lie group of dimension 3 with applications in geometry, topology, representation theory, and physics. SL(2, R) acts on the complex upper half-plane by fractional linear transformations. The group action factors through the quotient PSL(2, R) (the 2 × 2 projective special linear group over R). More specifically, :PSL(2, R) = SL(2, R) / , where ''I'' denotes the 2 × 2 identity matrix. It contains the modular group PSL(2, Z). Also closely related is the 2-fold covering group, Mp(2, R), a metaplectic group (thinking of SL(2, R) as a symplectic group). Another related group is SL±(2, R), the group of real 2 × 2 matrices with determinant ±1; this is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartan Matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. Amusingly, the Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan. Lie algebras A (symmetrizable) generalized Cartan matrix is a square matrix A = (a_) with integral entries such that # For diagonal entries, a_ = 2 . # For non-diagonal entries, a_ \leq 0 . # a_ = 0 if and only if a_ = 0 # A can be written as DS, where D is a diagonal matrix, and S is a symmetric matrix. For example, the Cartan matrix for ''G''2 can be decomposed as such: : \begin 2 & -3 \\ -1 & 2 \end = \begin 3&0\\ 0&1 \end\begin \frac & -1 \\ -1 & 2 \end. The third condition is not independent but is really a consequence of the first and fourth conditions. We can always choose a ''D'' with positive diagonal entries. In that case, if ''S'' in the ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
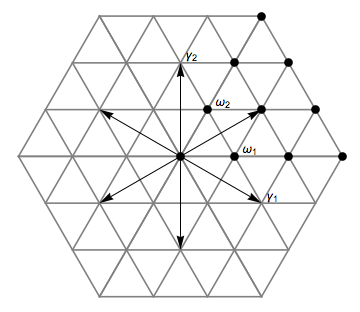
Simple Root (root System)
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and representation theory of semisimple Lie algebras. Since Lie groups (and some analogues such as algebraic groups) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory). Finally, root systems are important for their own sake, as in spectral graph theory. Definitions and examples As a first example, consider the six vectors in 2-dimensional Euclidean space, R2, as shown in the image at the right; call them roots. These vectors span the whole s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weight (representation Theory)
In the mathematical field of representation theory, a weight of an algebra ''A'' over a field F is an algebra homomorphism from ''A'' to F, or equivalently, a one-dimensional representation of ''A'' over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space. Motivation and general concept Given a set ''S'' of n\times n matrices over the same field, each of which is diagonalizable, and any two of which commute, it is always possible to simultaneously diagonalize all of the elements of ''S''.In fact, given a set of commuting matrices over an algebraically closed field, they are simultaneously triangularizable, without needing to assume that they are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representation Theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices and their algebraic operations (for example, matrix addition, matrix multiplication). The theory of matrices and linear operators is well-understood, so representations of more abstract objects in terms of familiar linear algebra objects helps glean properties and sometimes simplify calculations on more abstract theories. The algebraic objects amenable to such a description include groups, associative algebras and Lie algebras. The most prominent of these (and historically the first) is the representation theory of groups, in which elements of a group are represented by invertible matrices in such a way that the group operation i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Class
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deformation being called a homotopy (, ; , ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the second p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |