|
Wallace Multiplier
A Wallace multiplier is a hardware implementation of a binary multiplier, a digital circuit that multiplies two integers. It uses a selection of full and half adders (the Wallace tree or Wallace reduction) to sum partial products in stages until two numbers are left. Wallace multipliers reduce as much as possible on each layer, whereas Dadda multipliers try to minimize the required number of gates by postponing the reduction to the upper layers. Wallace multipliers were devised by the Australian computer scientist Chris Wallace in 1964. The Wallace tree has three steps: # Multiply each bit of one of the arguments, by each bit of the other. # Reduce the number of partial products to two by layers of full and half adders. # Group the wires in two numbers, and add them with a conventional adder. Compared to naively adding partial products with regular adders, the benefit of the Wallace tree is its faster speed. It has O(\log n) reduction layers, but each layer has only O(1) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dadda Multiplier
The Dadda multiplier is a hardware binary multiplier design invented by computer scientist Luigi Dadda in 1965. It uses a selection of full and half adders to sum the partial products in stages (the Dadda tree or Dadda reduction) until two numbers are left. The design is similar to the Wallace multiplier, but the different reduction tree reduces the required number of gates (for all but the smallest operand sizes) and makes it slightly faster (for all operand sizes). Dadda and Wallace multipliers have the same three steps for two bit strings w_1 and w_2 of lengths \ell_1 and \ell_2 respectively: # Multiply (logical AND) each bit of w_1, by each bit of w_2, yielding \ell_1\cdot\ell_2 results, grouped by weight in columns # Reduce the number of partial products by stages of full and half adders until we are left with at most two bits of each weight. # Add the final result with a conventional adder. As with the Wallace multiplier, the multiplication products of the first step ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dadda Tree
The Dadda multiplier is a hardware binary multiplier design invented by computer scientist Luigi Dadda in 1965. It uses a selection of full and half adders to sum the partial products in stages (the Dadda tree or Dadda reduction) until two numbers are left. The design is similar to the Wallace multiplier, but the different reduction tree reduces the required number of gates (for all but the smallest operand sizes) and makes it slightly faster (for all operand sizes). Dadda and Wallace multipliers have the same three steps for two bit strings w_1 and w_2 of lengths \ell_1 and \ell_2 respectively: # Multiply (logical AND) each bit of w_1, by each bit of w_2, yielding \ell_1\cdot\ell_2 results, grouped by weight in columns # Reduce the number of partial products by stages of full and half adders until we are left with at most two bits of each weight. # Add the final result with a conventional adder. As with the Wallace multiplier, the multiplication products of the first step c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Tree
In computer science, a binary tree is a k-ary k = 2 tree data structure in which each node has at most two children, which are referred to as the ' and the '. A recursive definition using just set theory notions is that a (non-empty) binary tree is a tuple (''L'', ''S'', ''R''), where ''L'' and ''R'' are binary trees or the empty set and ''S'' is a singleton set containing the root. Some authors allow the binary tree to be the empty set as well. From a graph theory perspective, binary (and K-ary) trees as defined here are arborescences. A binary tree may thus be also called a bifurcating arborescence—a term which appears in some very old programming books, before the modern computer science terminology prevailed. It is also possible to interpret a binary tree as an undirected, rather than a directed graph, in which case a binary tree is an ordered, rooted tree. Some authors use rooted binary tree instead of ''binary tree'' to emphasize the fact that the tree is rooted, bu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Booth Encoding
Booth's multiplication algorithm is a multiplication algorithm that multiplies two signed binary numbers in two's complement notation. The algorithm was invented by Andrew Donald Booth in 1950 while doing research on crystallography at Birkbeck College in Bloomsbury, London. Booth's algorithm is of interest in the study of computer architecture. The algorithm Booth's algorithm examines adjacent pairs of bits of the 'N'-bit multiplier ''Y'' in signed two's complement representation, including an implicit bit below the least significant bit, ''y''−1 = 0. For each bit ''y''''i'', for ''i'' running from 0 to ''N'' − 1, the bits ''y''''i'' and ''y''''i''−1 are considered. Where these two bits are equal, the product accumulator ''P'' is left unchanged. Where ''y''''i'' = 0 and ''y''''i''−1 = 1, the multiplicand times 2''i'' is added to ''P''; and where ''y''i = 1 and ''y''i−1 = 0, the multiplicand times 2''i'' is subtracted from ''P''. The final value of ''P'' is the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplication
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a ''product''. The multiplication of whole numbers may be thought of as repeated addition; that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, the ''multiplicand'', as the quantity of the other one, the ''multiplier''. Both numbers can be referred to as ''factors''. :a\times b = \underbrace_ For example, 4 multiplied by 3, often written as 3 \times 4 and spoken as "3 times 4", can be calculated by adding 3 copies of 4 together: :3 \times 4 = 4 + 4 + 4 = 12 Here, 3 (the ''multiplier'') and 4 (the ''multiplicand'') are the ''factors'', and 12 is the ''product''. One of the main properties of multiplication is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Arithmetic
In computing, an arithmetic logic unit (ALU) is a combinational digital circuit that performs arithmetic and bitwise operations on integer binary numbers. This is in contrast to a floating-point unit (FPU), which operates on floating point numbers. It is a fundamental building block of many types of computing circuits, including the central processing unit (CPU) of computers, FPUs, and graphics processing units (GPUs). The inputs to an ALU are the data to be operated on, called operands, and a code indicating the operation to be performed; the ALU's output is the result of the performed operation. In many designs, the ALU also has status inputs or outputs, or both, which convey information about a previous operation or the current operation, respectively, between the ALU and external status registers. Signals An ALU has a variety of input and output nets, which are the electrical conductors used to convey digital signals between the ALU and external circuitry. When an ALU is o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Logic Circuits
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today. History The prehistory of arithmetic is limited to a small number of artifacts, which may indicate the conception of addition and subtraction, the best-known being the Ishango bone from central Africa, dating from somewhere between 20,000 and 18,000 BC, although its interpretation is disputed. The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations: addition, subtraction, multiplication, and division, as early as 2000 BC. These artifacts do not always reveal the specific process used for solving problems, but t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IEEE Transactions On Electronic Computers
''IEEE Transactions on Computers'' is a monthly peer-reviewed scientific journal covering all aspects of computer design. It was established in 1952 and is published by the IEEE Computer Society. The editor-in-chief is Ahmed Louri, David and Marilyn Karlgaard Endowed Chair Professor of Electrical and Computer Engineering, George Washington University. According to the ''Journal Citation Reports'', the journal has a 2019 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 3.131. References External links * Transactions on Computers Computer science journals English-language journals Publications established in 1952 Monthly journals {{comp-sci-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
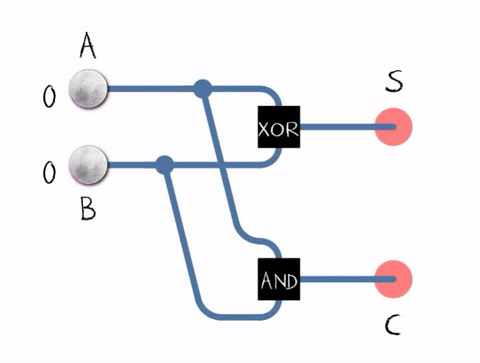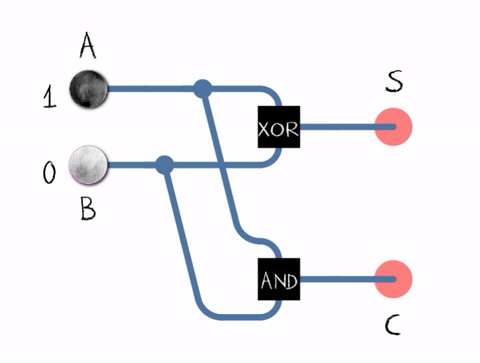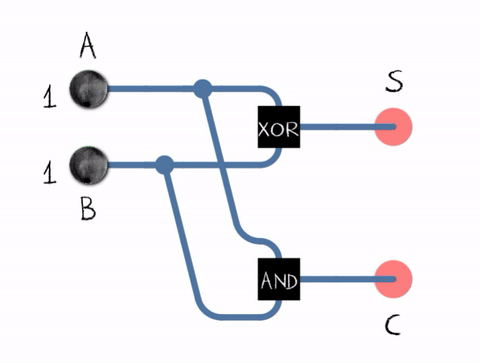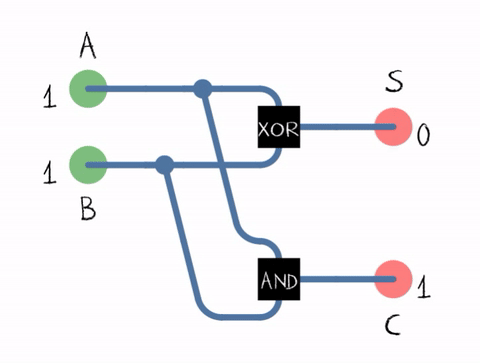
Half Adder
An adder, or summer, is a digital circuit that performs addition of numbers. In many computers and other kinds of processors adders are used in the arithmetic logic units (ALUs). They are also used in other parts of the processor, where they are used to calculate addresses, table indices, increment and decrement operators and similar operations. Although adders can be constructed for many number representations, such as binary-coded decimal or excess-3, the most common adders operate on binary numbers. In cases where two's complement or ones' complement is being used to represent negative numbers, it is trivial to modify an adder into an adder–subtractor. Other signed number representations require more logic around the basic adder. Binary adders Half adder The half adder adds two single binary digits ''A'' and ''B''. It has two outputs, sum (''S'') and carry (''C''). The carry signal represents an overflow into the next digit of a multi-digit addition. The value of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Full Adder
An adder, or summer, is a digital circuit that performs addition of numbers. In many computers and other kinds of processors adders are used in the arithmetic logic units (ALUs). They are also used in other parts of the processor, where they are used to calculate addresses, table indices, increment and decrement operators and similar operations. Although adders can be constructed for many number representations, such as binary-coded decimal or excess-3, the most common adders operate on binary numbers. In cases where two's complement or ones' complement is being used to represent negative numbers, it is trivial to modify an adder into an adder–subtractor. Other signed number representations require more logic around the basic adder. Binary adders Half adder The half adder adds two single binary digits ''A'' and ''B''. It has two outputs, sum (''S'') and carry (''C''). The carry signal represents an overflow into the next digit of a multi-digit addition. The value of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long Multiplication
A multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient than others. Efficient multiplication algorithms have existed since the advent of the decimal system. Long multiplication If a positional numeral system is used, a natural way of multiplying numbers is taught in schools as long multiplication, sometimes called grade-school multiplication, sometimes called the Standard Algorithm: multiply the multiplicand by each digit of the multiplier and then add up all the properly shifted results. It requires memorization of the multiplication table for single digits. This is the usual algorithm for multiplying larger numbers by hand in base 10. A person doing long multiplication on paper will write down all the products and then add them together; an abacus-user will sum the products as soon as each one is computed. Example This example uses ''long multiplication'' to multiply 23,958 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gate Delay
Propagation delay is the time duration taken for a signal to reach its destination. It can relate to networking, electronics or physics. ''Hold time'' is the minimum interval required for the logic level to remain on the input after triggering edge of the clock pulse. Networking In computer networks, propagation delay is the amount of time it takes for the head of the signal to travel from the sender to the receiver. It can be computed as the ratio between the link length and the propagation speed over the specific medium. Propagation delay is equal to ''d / s'' where ''d'' is the distance and ''s'' is the wave propagation speed. In wireless communication, ''s''=''c'', i.e. the speed of light. In copper wire, the speed ''s'' generally ranges from .59c to .77c. This delay is the major obstacle in the development of high-speed computers and is called the interconnect bottleneck in IC systems. Electronics In electronics, digital circuits and digital electronics, the propagati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |